|
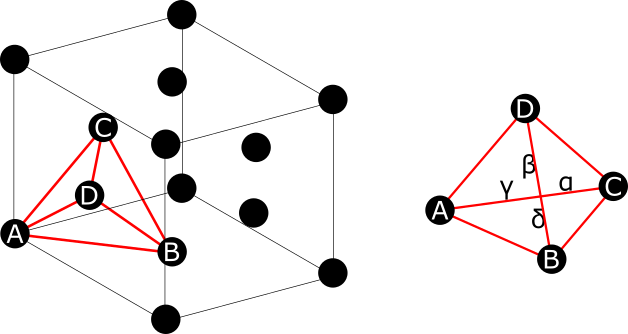
Stacking Fault
In crystallography, a stacking fault is a planar defect that can occur in crystalline materials.Fine, Morris E. (1921). "Introduction to Chemical and Structural Defects in Crystalline Solids", in ''Treatise on Solid State Chemistry Volume 1'', Springer. Crystalline materials form repeating patterns of layers of atoms. Errors can occur in the sequence of these layers and are known as stacking faults. Stacking faults are in a higher energy state which is quantified by the formation enthalpy per unit area called the stacking-fault energy. Stacking faults can arise during crystal growth or from plastic deformation. In addition, dislocations in low stacking-fault energy materials typically dissociate into an ''extended dislocation'', which is a stacking fault bounded by partial dislocations. The most common example of stacking faults is found in close-packed crystal structures. Face-centered cubic (fcc) structures differ from hexagonal close packed (hcp) structures only in stacking ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schema Fcc Hcp
Schema may refer to: Science and technology * SCHEMA (bioinformatics), an algorithm used in protein engineering * Schema (genetic algorithms), a set of programs or bit strings that have some genotypic similarity * Schema.org, a web markup vocabulary * Schema (logic) ** Axiom schema, in formal logic * Image schema, a recurring pattern of spatial sensory experience * Database schema * XML schema Other * Body schema, a neural representation of one's own bodily posture * Galant Schemata, stock phrases in Galant music * Schema (Kant), in philosophy * Schema (psychology), a mental set or representation * Schema Records, a jazz record label in Milan, Italy *, a solemn vow of asceticism of a monk in Orthodox monasticism ** Great Schema, the highest degree of Orthodox monasticism * ''Schema'' (fly), a genus of insects See also * Scheme (other) * Schematic * Skema (other) SKEMA Business School ("School of Knowledge Economy and Management") is a leading French busi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystallography
Crystallography is the branch of science devoted to the study of molecular and crystalline structure and properties. The word ''crystallography'' is derived from the Ancient Greek word (; "clear ice, rock-crystal"), and (; "to write"). In July 2012, the United Nations recognised the importance of the science of crystallography by proclaiming 2014 the International Year of Crystallography.UN announcement "International Year of Crystallography" iycr2014.org. 12 July 2012 Crystallography is a broad topic, and many of its subareas, such as X-ray crystallography, are themselves important scientific topics. Crystallography ranges from the fundamentals of crystal structure to the mathematics of Crystal system, crystal geometry, including those that are Aperiodic crystal, not periodic or quasi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystallographic Defect
A crystallographic defect is an interruption of the regular patterns of arrangement of atoms or molecules in Crystal, crystalline solids. The positions and orientations of particles, which are repeating at fixed distances determined by the Crystal structure#unit cell, unit cell parameters in crystals, exhibit a periodic crystal structure, but this is usually imperfect.Ehrhart, P. (1991Properties and interactions of atomic defects in metals and alloys, volume 25 of Landolt-Börnstein, New Series III, chapter 2, p. 88, Springer, Berlin Several types of defects are often characterized: point defects, line defects, planar defects, bulk defects. Topological homotopy establishes a mathematical method of characterization. Point defects Point defects are defects that occur only at or around a single lattice point. They are not extended in space in any dimension. Strict limits for how small a point defect is are generally not defined explicitly. However, these defects typically involve at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enthalpy
Enthalpy () is the sum of a thermodynamic system's internal energy and the product of its pressure and volume. It is a state function in thermodynamics used in many measurements in chemical, biological, and physical systems at a constant external pressure, which is conveniently provided by the large ambient atmosphere. The pressure–volume term expresses the work (physics), work W that was done against constant external pressure P_\text to establish the system's physical dimensions from V_\text=0 to some final volume V_\text (as W=P_\text\Delta V), i.e. to make room for it by displacing its surroundings. The pressure-volume term is very small for solids and liquids at common conditions, and fairly small for gases. Therefore, enthalpy is a stand-in for energy in chemical systems; Bond energy, bond, Lattice energy, lattice, solvation, and other chemical "energies" are actually enthalpy differences. As a state function, enthalpy depends only on the final configuration of internal e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dislocations
In materials science, a dislocation or Taylor's dislocation is a linear crystallographic defect or irregularity within a crystal structure that contains an abrupt change in the arrangement of atoms. The movement of dislocations allow atoms to slide over each other at low stress levels and is known as ''glide'' or Slip (materials science), slip. The crystalline order is restored on either side of a ''glide dislocation'' but the atoms on one side have moved by one position. The crystalline order is not fully restored with a ''partial dislocation''. A dislocation defines the boundary between ''slipped'' and ''unslipped'' regions of material and as a result, must either form a complete loop, intersect other dislocations or defects, or extend to the edges of the crystal. A dislocation can be characterised by the distance and direction of movement it causes to atoms which is defined by the Burgers vector. Plasticity (physics), Plastic deformation of a material occurs by the creation and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Dislocations
In materials science, a partial dislocation is a decomposed form of dislocation that occurs within a crystalline material. An ''extended dislocation'' is a dislocation that has dissociated into a pair of partial dislocations. The vector sum of the Burgers vectors of the partial dislocations is the Burgers vector of the extended dislocation. Reaction favorability A dislocation will decompose into partial dislocations if the energy state of the sum of the partials is less than the energy state of the original dislocation. This is summarized by ''Frank's Energy Criterion'': : \begin , \boldsymbol, ^2>&, \boldsymbol, ^2+, \boldsymbol, ^2 \text\\ , \boldsymbol, ^2& , \frac \sqrt, ^2+, \frac \sqrt, ^2\\ \frac >& \frac+\frac \end The components of the ''Shockley Partials'' must add up to the original vector that is being decomposed: : \begin \frac (1) =& \frac(2)+\frac(1)\\ \frac (0) =& \frac(-1)+\frac(1)\\ \frac (-1) =& \frac(-1)+\frac(-2) \end Frank partial dislocations ''Frank p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Face-centered Cubic
In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of these crystals: *Primitive cubic (abbreviated ''cP'' and alternatively called simple cubic) *Body-centered cubic (abbreviated ''cI'' or bcc) *Face-centered cubic (abbreviated ''cF'' or fcc) Note: the term fcc is often used in synonym for the ''cubic close-packed'' or ccp structure occurring in metals. However, fcc stands for a face-centered cubic Bravais lattice, which is not necessarily close-packed when a motif is set onto the lattice points. E.g. the diamond and the zincblende lattices are fcc but not close-packed. Each is subdivided into other variants listed below. Although the ''unit cells'' in these crystals are conventionally taken to be cubes, the primitive unit cells often are not. Bravais lattices The three Bravais latices ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagonal Close Packed
In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement (or lattice). Carl Friedrich Gauss proved that the highest average density – that is, the greatest fraction of space occupied by spheres – that can be achieved by a lattice packing is :\frac \approx 0.74048. The same packing density can also be achieved by alternate stackings of the same close-packed planes of spheres, including structures that are aperiodic in the stacking direction. The Kepler conjecture states that this is the highest density that can be achieved by any arrangement of spheres, either regular or irregular. This conjecture was proven by Thomas Hales. The highest density is so far known only for 1, 2, 3, 8, and 24 dimensions. Many crystal structures are based on a close-packing of a single kind of atom, or a close-packing of large ions with smaller ions filling the spaces between them. The cubic and hexagonal arrangements are very cl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Modulus
In materials science, shear modulus or modulus of rigidity, denoted by ''G'', or sometimes ''S'' or ''μ'', is a measure of the Elasticity (physics), elastic shear stiffness of a material and is defined as the ratio of shear stress to the shear strain: :G \ \stackrel\ \frac = \frac = \frac where :\tau_ = F/A \, = shear stress :F is the force which acts :A is the area on which the force acts :\gamma_ = shear strain. In engineering :=\Delta x/l = \tan \theta , elsewhere := \theta :\Delta x is the transverse displacement :l is the initial length of the area. The derived SI unit of shear modulus is the Pascal (unit), pascal (Pa), although it is usually expressed in Pascal (unit), gigapascals (GPa) or in thousand pounds per square inch (ksi). Its dimensional analysis, dimensional form is M1L−1T−2, replacing ''force'' by ''mass'' times ''acceleration''. Explanation The shear modulus is one of several quantities for measuring the stiffness of materials. All of them arise in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Semiconductors
Semiconductor materials are nominally small band gap insulators. The defining property of a semiconductor material is that it can be compromised by doping it with impurities that alter its electronic properties in a controllable way. Because of their application in the computer and photovoltaic industry—in devices such as transistors, lasers, and solar cells—the search for new semiconductor materials and the improvement of existing materials is an important field of study in materials science. Most commonly used semiconductor materials are crystalline inorganic solids. These materials are classified according to the periodic table groups of their constituent atoms. Different semiconductor materials differ in their properties. Thus, in comparison with silicon, compound semiconductors have both advantages and disadvantages. For example, gallium arsenide (GaAs) has six times higher electron mobility than silicon, which allows faster operation; wider band gap, which allows ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |