|
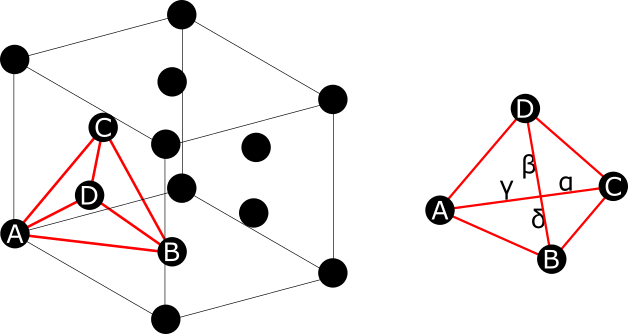
Stacking Fault
In crystallography, a stacking fault is a planar defect that can occur in crystalline materials.Fine, Morris E. (1921). "Introduction to Chemical and Structural Defects in Crystalline Solids", in ''Treatise on Solid State Chemistry Volume 1'', Springer. Crystalline materials form repeating patterns of layers of atoms. Errors can occur in the sequence of these layers and are known as stacking faults. Stacking faults are in a higher energy state which is quantified by the formation enthalpy per unit area called the stacking-fault energy. Stacking faults can arise during crystal growth or from plastic deformation. In addition, dislocations in low stacking-fault energy materials typically dissociate into an ''extended dislocation'', which is a stacking fault bounded by partial dislocations. The most common example of stacking faults is found in close-packed crystal structures. Face-centered cubic (fcc) structures differ from hexagonal close packed (hcp) structures only in stacking ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schema Fcc Hcp
The word schema comes from the Greek word ('), which means ''shape'', or more generally, ''plan''. The plural is ('). In English, both ''schemas'' and ''schemata'' are used as plural forms. Schema may refer to: Science and technology * SCHEMA (bioinformatics), an algorithm used in protein engineering * Schema (genetic algorithms), a set of programs or bit strings that have some genotypic similarity * Schema.org, a web markup vocabulary * Schema (logic) ** Axiom schema, in formal logic * Image schema, a recurring pattern of spatial sensory experience * Database schema * XML schema Other * Body schema, a neural representation of one's own bodily posture * Galant Schemata, stock phrases in Galant music * Schema (Kant), in philosophy * Schema (psychology), a mental set or representation * Schema Records, a jazz record label in Milan, Italy *, a solemn vow of asceticism of a monk in Orthodox monasticism ** Great Schema, the highest degree of Orthodox monasticism * ''Schema'' (f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystallography
Crystallography is the experimental science of determining the arrangement of atoms in crystalline solids. Crystallography is a fundamental subject in the fields of materials science and solid-state physics (condensed matter physics). The word "crystallography" is derived from the Greek word κρύσταλλος (''krystallos'') "clear ice, rock-crystal", with its meaning extending to all solids with some degree of transparency, and γράφειν (''graphein'') "to write". In July 2012, the United Nations recognised the importance of the science of crystallography by proclaiming that 2014 would be the International Year of Crystallography. denote a direction vector (in real space). * Coordinates in ''angle brackets'' or ''chevrons'' such as <100> denote a ''family'' of directions which are related by symmetry operations. In the cubic crystal system for example, would mean 00 10 01/nowiki> or the negative of any of those directions. * Miller indices in ''parentheses ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystallographic Defect
A crystallographic defect is an interruption of the regular patterns of arrangement of atoms or molecules in crystalline solids. The positions and orientations of particles, which are repeating at fixed distances determined by the unit cell parameters in crystals, exhibit a periodic crystal structure, but this is usually imperfect.Ehrhart, P. (1991Properties and interactions of atomic defects in metals and alloys, volume 25 of Landolt-Börnstein, New Series III, chapter 2, p. 88, Springer, Berlin Several types of defects are often characterized: point defects, line defects, planar defects, bulk defects. Topological homotopy establishes a mathematical method of characterization. Point defects Point defects are defects that occur only at or around a single lattice point. They are not extended in space in any dimension. Strict limits for how small a point defect is are generally not defined explicitly. However, these defects typically involve at most a few extra or missing atoms. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enthalpy
Enthalpy , a property of a thermodynamic system, is the sum of the system's internal energy and the product of its pressure and volume. It is a state function used in many measurements in chemical, biological, and physical systems at a constant pressure, which is conveniently provided by the large ambient atmosphere. The pressure–volume term expresses the work required to establish the system's physical dimensions, i.e. to make room for it by displacing its surroundings. The pressure-volume term is very small for solids and liquids at common conditions, and fairly small for gases. Therefore, enthalpy is a stand-in for energy in chemical systems; bond, lattice, solvation and other "energies" in chemistry are actually enthalpy differences. As a state function, enthalpy depends only on the final configuration of internal energy, pressure, and volume, not on the path taken to achieve it. In the International System of Units (SI), the unit of measurement for enthalpy is the j ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stacking-fault Energy
The stacking-fault energy (SFE) is a materials property on a very small scale. It is noted as γSFE in units of energy per area. A stacking fault is an interruption of the normal stacking sequence of atomic planes in a close-packed crystal structure. These interruptions carry a certain stacking-fault energy. The width of stacking fault is a consequence of the balance between the repulsive force between two partial dislocations on one hand and the attractive force due to the surface tension of the stacking fault on the other hand. The equilibrium width is thus partially determined by the stacking-fault energy. When the SFE is high the dissociation of a full dislocation into two partials is energetically unfavorable, and the material can deform either by dislocation glide or cross-slip. Lower SFE materials display wider stacking faults and have more difficulties for cross-slip. The SFE modifies the ability of a dislocation in a crystal to glide onto an intersecting slip plane. When t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dislocations
In materials science, a dislocation or Taylor's dislocation is a linear crystallographic defect or irregularity within a crystal structure that contains an abrupt change in the arrangement of atoms. The movement of dislocations allow atoms to slide over each other at low stress levels and is known as ''glide'' or slip. The crystalline order is restored on either side of a ''glide dislocation'' but the atoms on one side have moved by one position. The crystalline order is not fully restored with a ''partial dislocation''. A dislocation defines the boundary between ''slipped'' and ''unslipped'' regions of material and as a result, must either form a complete loop, intersect other dislocations or defects, or extend to the edges of the crystal. A dislocation can be characterised by the distance and direction of movement it causes to atoms which is defined by the Burgers vector. Plastic deformation of a material occurs by the creation and movement of many dislocations. The number an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Dislocations
In materials science, a partial dislocation is a decomposed form of dislocation that occurs within a crystalline material. An ''extended dislocation'' is a dislocation that has dissociated into a pair of partial dislocations. The vector sum of the Burgers vectors of the partial dislocations is the Burgers vector of the extended dislocation. Reaction favorability A dislocation will decompose into partial dislocations if the energy state of the sum of the partials is less than the energy state of the original dislocation. This is summarized by ''Frank's Energy Criterion'': : \begin , \boldsymbol, ^2>&, \boldsymbol, ^2+, \boldsymbol, ^2 \text\\ , \boldsymbol, ^2& , \frac \sqrt, ^2+, \frac \sqrt, ^2\\ \frac >& \frac+\frac \end The components of the ''Shockley Partials'' must add up to the original vector that is being decomposed: : \begin \frac (1) =& \frac(2)+\frac(1)\\ \frac (0) =& \frac(-1)+\frac(1)\\ \frac (-1) =& \frac(-1)+\frac(-2) \end Frank partial dislocations ''Frank ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Face-centered Cubic
In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of these crystals: *Primitive cubic (abbreviated ''cP'' and alternatively called simple cubic) *Body-centered cubic (abbreviated ''cI'' or bcc) *Face-centered cubic (abbreviated ''cF'' or fcc, and alternatively called ''cubic close-packed'' or ccp) Each is subdivided into other variants listed below. Although the ''unit cells'' in these crystals are conventionally taken to be cubes, the primitive unit cells often are not. Bravais lattices The three Bravais lattices in the cubic crystal system are: The primitive cubic lattice (cP) consists of one lattice point on each corner of the cube; this means each simple cubic unit cell has in total one lattice point. Each atom at a lattice point is then shared equally between eight adjacent cub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagonal Close Packed
In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement (or lattice). Carl Friedrich Gauss proved that the highest average density – that is, the greatest fraction of space occupied by spheres – that can be achieved by a lattice packing is :\frac \approx 0.74048. The same packing density can also be achieved by alternate stackings of the same close-packed planes of spheres, including structures that are aperiodic in the stacking direction. The Kepler conjecture states that this is the highest density that can be achieved by any arrangement of spheres, either regular or irregular. This conjecture was proven by T. C. Hales. Highest density is known only for 1, 2, 3, 8, and 24 dimensions. Many crystal structures are based on a close-packing of a single kind of atom, or a close-packing of large ions with smaller ions filling the spaces between them. The cubic and hexagonal arrangements are very close to one ano ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Modulus
In materials science, shear modulus or modulus of rigidity, denoted by ''G'', or sometimes ''S'' or ''μ'', is a measure of the elastic shear stiffness of a material and is defined as the ratio of shear stress to the shear strain: :G \ \stackrel\ \frac = \frac = \frac where :\tau_ = F/A \, = shear stress :F is the force which acts :A is the area on which the force acts :\gamma_ = shear strain. In engineering :=\Delta x/l = \tan \theta , elsewhere := \theta :\Delta x is the transverse displacement :l is the initial length of the area. The derived SI unit of shear modulus is the pascal (Pa), although it is usually expressed in gigapascals (GPa) or in thousand pounds per square inch (ksi). Its dimensional form is M1L−1T−2, replacing ''force'' by ''mass'' times ''acceleration''. Explanation The shear modulus is one of several quantities for measuring the stiffness of materials. All of them arise in the generalized Hooke's law: * Young's modulus ''E'' describes t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Semiconductors
Semiconductor materials are nominally small band gap insulators. The defining property of a semiconductor material is that it can be compromised by doping it with impurities that alter its electronic properties in a controllable way. Because of their application in the computer and photovoltaic industry—in devices such as transistors, lasers, and solar cells—the search for new semiconductor materials and the improvement of existing materials is an important field of study in materials science. Most commonly used semiconductor materials are crystalline inorganic solids. These materials are classified according to the periodic table groups of their constituent atoms. Different semiconductor materials differ in their properties. Thus, in comparison with silicon, compound semiconductors have both advantages and disadvantages. For example, gallium arsenide (GaAs) has six times higher electron mobility than silicon, which allows faster operation; wider band gap, which allows o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |