|
Spin Waves
A spin wave is a propagating disturbance in the ordering of a magnetic material. These low-lying collective excitations occur in magnetic lattices with continuous symmetry. From the equivalent quasiparticle point of view, spin waves are known as magnons, which are bosonic modes of the spin lattice that correspond roughly to the phonon excitations of the nuclear lattice. As temperature is increased, the thermal excitation of spin waves reduces a ferromagnet's spontaneous magnetization. The energies of spin waves are typically only in keeping with typical Curie points at room temperature and below. Theory The simplest way of understanding spin waves is to consider the Hamiltonian \mathcal for the Heisenberg ferromagnet: :\mathcal = -\frac J \sum_ \mathbf_i \cdot \mathbf_j - g \mu_ \sum_i \mathbf \cdot \mathbf_i where is the exchange energy, the operators represent the spins at Bravais lattice points, is the Landé -factor, is the Bohr magneton and is the internal field ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Collective Excitation
In physics, quasiparticles and collective excitations are closely related emergent phenomena arising when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in vacuum. For example, as an electron travels through a semiconductor, its motion is disturbed in a complex way by its interactions with other electrons and with atomic nuclei. The electron behaves as though it has a different effective mass travelling unperturbed in vacuum. Such an electron is called an ''electron quasiparticle''. In another example, the aggregate motion of electrons in the valence band of a semiconductor or a hole band in a metal behave as though the material instead contained positively charged quasiparticles called ''electron holes''. Other quasiparticles or collective excitations include the ''phonon'', a quasiparticle derived from the vibrations of atoms in a solid, and the ''plasmons'', a particle derived from plasma oscillation. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heisenberg Model (quantum)
The quantum Heisenberg model, developed by Werner Heisenberg, is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spins of the magnetic systems are treated quantum mechanically. It is related to the prototypical Ising model, where at each site of a lattice, a spin \sigma_i \in \ represents a microscopic magnetic dipole to which the magnetic moment is either up or down. Except the coupling between magnetic dipole moments, there is also a multipolar version of Heisenberg model called the multipolar exchange interaction. Overview For quantum mechanical reasons (see exchange interaction or ), the dominant coupling between two dipoles may cause nearest-neighbors to have lowest energy when they are ''aligned''. Under this assumption (so that magnetic interactions only occur between adjacent dipoles) and on a 1-dimensional periodic lattice, the Hamiltonian can be written in the form :\hat H = -J \sum_^ \sig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Light
Light or visible light is electromagnetic radiation that can be perceived by the human eye. Visible light is usually defined as having wavelengths in the range of 400–700 nanometres (nm), corresponding to frequencies of 750–420 terahertz, between the infrared (with longer wavelengths) and the ultraviolet (with shorter wavelengths). In physics, the term "light" may refer more broadly to electromagnetic radiation of any wavelength, whether visible or not. In this sense, gamma rays, X-rays, microwaves and radio waves are also light. The primary properties of light are intensity, propagation direction, frequency or wavelength spectrum and polarization. Its speed in a vacuum, 299 792 458 metres a second (m/s), is one of the fundamental constants of nature. Like all types of electromagnetic radiation, visible light propagates by massless elementary particles called photons that represents the quanta of electromagnetic field, and can be analyzed as both waves and par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inelastic Neutron Scattering
Neutron scattering, the irregular dispersal of free neutrons by matter, can refer to either the naturally occurring physical process itself or to the man-made experimental techniques that use the natural process for investigating materials. The natural/physical phenomenon is of elemental importance in nuclear engineering and the nuclear sciences. Regarding the experimental technique, understanding and manipulating neutron scattering is fundamental to the applications used in crystallography, physics, physical chemistry, biophysics, and materials research. Neutron scattering is practiced at research reactors and spallation neutron sources that provide neutron radiation of varying intensities. Neutron diffraction (elastic scattering) techniques are used for analyzing structures; where inelastic neutron scattering is used in studying atomic vibrations and other excitations. Scattering of fast neutrons "Fast neutrons" (see neutron temperature) have a kinetic energy above ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time-reversal Symmetry
T-symmetry or time reversal symmetry is the theoretical symmetry of physical laws under the transformation of time reversal, : T: t \mapsto -t. Since the second law of thermodynamics states that entropy increases as time flows toward the future, in general, the macroscopic universe does not show symmetry under time reversal. In other words, time is said to be non-symmetric, or asymmetric, except for special equilibrium states when the second law of thermodynamics predicts the time symmetry to hold. However, quantum noninvasive measurements are predicted to violate time symmetry even in equilibrium, contrary to their classical counterparts, although this has not yet been experimentally confirmed. Time ''asymmetries'' generally are caused by one of three categories: # intrinsic to the dynamic physical law (e.g., for the weak force) # due to the initial conditions of the universe (e.g., for the second law of thermodynamics) # due to measurements (e.g., for the noninvasive measur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Transition
In chemistry, thermodynamics, and other related fields, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic states of matter: solid, liquid, and gas, and in rare cases, plasma. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change as a result of the change of external conditions, such as temperature or pressure. This can be a discontinuous change; for example, a liquid may become gas upon heating to its boiling point, resulting in an abrupt change in volume. The identification of the external conditions at which a transformation occurs defines the phase transition point. Types of phase transition At the phase transition point for a substance, for instance the boiling point, the two phases involved - liquid and vapor, have identic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Stiffness
The spin stiffness or spin rigidity or helicity modulus or the "superfluid density" (for bosons the superfluid density is proportional to the spin stiffness) is a constant which represents the change in the ground state energy of a spin system as a result of introducing a slow in plane twist of the spins. The importance of this constant is in its use as an indicator of quantum phase transitions—specifically in models with metal-insulator transitions such as Mott insulators. It is also related to other topological invariants such as the Berry phase and Chern numbers as in the Quantum Hall effect. Mathematically Mathematically it can be defined by the following equation: :\rho_s = \cfrac\cfrac, _ where E_0 is the ground state energy, \theta is the twisting angle, and N is the number of lattice sites. Spin stiffness of the Heisenberg model Start off with the simple Heisenberg spin Hamiltonian: :H_\mathrm = -J \sum_ \left _i^z S_j^z + \cfrac(S_i^+ S_j^- + S_i^- S_j^+)\right/math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dispersion Relation
In the physical sciences and electrical engineering, dispersion relations describe the effect of dispersion on the properties of waves in a medium. A dispersion relation relates the wavelength or wavenumber of a wave to its frequency. Given the dispersion relation, one can calculate the phase velocity and group velocity of waves in the medium, as a function of frequency. In addition to the geometry-dependent and material-dependent dispersion relations, the overarching Kramers–Kronig relations describe the frequency dependence of wave propagation and attenuation. Dispersion may be caused either by geometric boundary conditions (waveguides, shallow water) or by interaction of the waves with the transmitting medium. Elementary particles, considered as matter waves, have a nontrivial dispersion relation even in the absence of geometric constraints and other media. In the presence of dispersion, wave velocity is no longer uniquely defined, giving rise to the distinction of phase ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
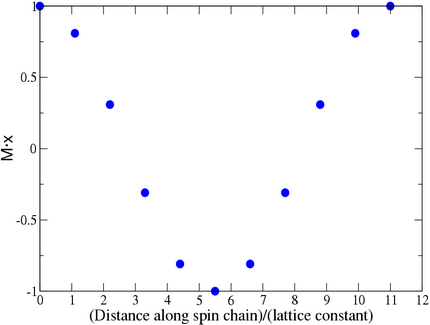
Spin Wave
A spin wave is a propagating disturbance in the ordering of a magnetic material. These low-lying collective excitations occur in magnetic lattices with continuous symmetry. From the equivalent quasiparticle point of view, spin waves are known as magnons, which are bosonic modes of the spin lattice that correspond roughly to the phonon excitations of the nuclear lattice. As temperature is increased, the thermal excitation of spin waves reduces a ferromagnet's spontaneous magnetization. The energies of spin waves are typically only in keeping with typical Curie points at room temperature and below. Theory The simplest way of understanding spin waves is to consider the Hamiltonian \mathcal for the Heisenberg ferromagnet: :\mathcal = -\frac J \sum_ \mathbf_i \cdot \mathbf_j - g \mu_ \sum_i \mathbf \cdot \mathbf_i where is the exchange energy, the operators represent the spins at Bravais lattice points, is the Landé -factor, is the Bohr magneton and is the internal fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spontaneous Symmetry Breaking
Spontaneous symmetry breaking is a spontaneous process of symmetry breaking, by which a physical system in a symmetric state spontaneously ends up in an asymmetric state. In particular, it can describe systems where the equations of motion or the Lagrangian obey symmetries, but the lowest-energy vacuum solutions do not exhibit that same symmetry. When the system goes to one of those vacuum solutions, the symmetry is broken for perturbations around that vacuum even though the entire Lagrangian retains that symmetry. Overview By definition, spontaneous symmetry breaking requires the existence of physical laws (e.g. quantum mechanics) which are invariant under a symmetry transformation (such as translation or rotation), so that any pair of outcomes differing only by that transformation have the same probability distribution. For example if measurements of an observable at any two different positions have the same probability distribution, the observable has translational symmetry. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Symmetry
In mathematics and geometry, a discrete symmetry is a symmetry that describes non-continuous changes in a system. For example, a square possesses discrete rotational symmetry, as only rotations by multiples of right angles will preserve the square's original appearance. Discrete symmetries sometimes involve some type of 'swapping', these swaps usually being called ''reflections'' or ''interchanges''. In mathematics and theoretical physics, a discrete symmetry is a symmetry under the transformations of a discrete group—e.g. a topological group with a discrete topology whose elements form a finite or a countable set. One of the most prominent discrete symmetries in physics is parity symmetry. It manifests itself in various elementary physical quantum systems, such as quantum harmonic oscillator, electron orbitals of Hydrogen-like atoms by forcing wavefunctions to be even or odd. This in turn gives rise to selection rules that determine which transition lines are visible in atomic ab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Light")
.png "Click for more on -> Spontaneous Symmetry Breaking")