Spin Wave on:
[Wikipedia]
[Google]
[Amazon]
In

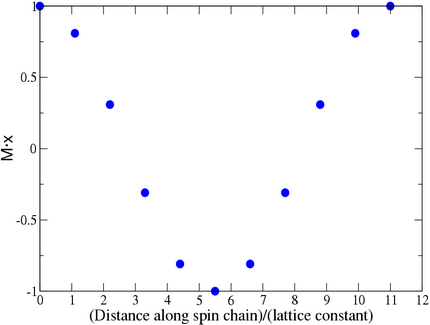 The simplest way of understanding spin waves is to consider the
The simplest way of understanding spin waves is to consider the
 In this model the magnetization
:
where is the volume. The propagation of spin waves is described by the Landau-Lifshitz equation of motion:
:
where is the gyromagnetic ratio and is the damping constant. The cross-products in this forbidding-looking equation show that the propagation of spin waves is governed by the torques generated by internal and external fields. (An equivalent form is the Landau-Lifshitz-Gilbert equation, which replaces the final term by a more "simple looking" equivalent one.)
The first term on the right hand side of the equation describes the precession of the magnetization under the influence of the applied field, while the above-mentioned final term describes how the magnetization vector "spirals in" towards the field direction as time progresses. In metals the damping forces described by the constant are in many cases dominated by the eddy currents.
One important difference between phonons and magnons lies in their
In this model the magnetization
:
where is the volume. The propagation of spin waves is described by the Landau-Lifshitz equation of motion:
:
where is the gyromagnetic ratio and is the damping constant. The cross-products in this forbidding-looking equation show that the propagation of spin waves is governed by the torques generated by internal and external fields. (An equivalent form is the Landau-Lifshitz-Gilbert equation, which replaces the final term by a more "simple looking" equivalent one.)
The first term on the right hand side of the equation describes the precession of the magnetization under the influence of the applied field, while the above-mentioned final term describes how the magnetization vector "spirals in" towards the field direction as time progresses. In metals the damping forces described by the constant are in many cases dominated by the eddy currents.
One important difference between phonons and magnons lies in their
Spin waves - The Feynman Lectures on Physics
performing Brillouin scattering measurements. Magnetic ordering Waves de:Spinwelle pl:Fale spinowe
condensed matter physics
Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid State of matter, phases, that arise from electromagnetic forces between atoms and elec ...
, a spin wave is a propagating disturbance in the ordering of a magnet
A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, steel, nickel, ...
ic material. These low-lying collective excitations occur in magnetic lattices with continuous symmetry
In mathematics, continuous symmetry is an intuitive idea corresponding to the concept of viewing some Symmetry in mathematics, symmetries as Motion (physics), motions, as opposed to discrete symmetry, e.g. reflection symmetry, which is invariant u ...
. From the equivalent quasiparticle
In condensed matter physics, a quasiparticle is a concept used to describe a collective behavior of a group of particles that can be treated as if they were a single particle. Formally, quasiparticles and collective excitations are closely relate ...
point of view, spin waves are known as magnons, which are boson
In particle physics, a boson ( ) is a subatomic particle whose spin quantum number has an integer value (0, 1, 2, ...). Bosons form one of the two fundamental classes of subatomic particle, the other being fermions, which have half odd-intege ...
ic modes of the spin lattice that correspond roughly to the phonon
A phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. In the context of optically trapped objects, the quantized vibration mode can be defined a ...
excitations of the nuclear lattice. As temperature is increased, the thermal excitation of spin waves reduces a ferromagnet
Ferromagnetism is a property of certain materials (such as iron) that results in a significant, observable magnetic permeability, and in many cases, a significant magnetic coercivity, allowing the material to form a permanent magnet. Ferromag ...
's spontaneous magnetization. The energies of spin waves are typically only in keeping with typical Curie point
In physics and materials science, the Curie temperature (''T''C), or Curie point, is the temperature above which certain materials lose their magnet, permanent magnetic properties, which can (in most cases) be replaced by magnetization, induced ...
s at room temperature and below.
Theory

 The simplest way of understanding spin waves is to consider the
The simplest way of understanding spin waves is to consider the Hamiltonian
Hamiltonian may refer to:
* Hamiltonian mechanics, a function that represents the total energy of a system
* Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system
** Dyall Hamiltonian, a modified Hamiltonian ...
for the Heisenberg
Werner Karl Heisenberg (; ; 5 December 1901 – 1 February 1976) was a German theoretical physicist, one of the main pioneers of the theory of quantum mechanics and a principal scientist in the German nuclear program during World War II.
He pub ...
ferromagnet:
:
where is the exchange energy, the operators represent the spins
The spins (as in having "the spins") is an adverse reaction of Substance intoxication, intoxication that causes a state of vertigo and nausea, causing one to feel as if "spinning out of control", especially when lying down. It is most commonly as ...
at Bravais lattice
In geometry and crystallography, a Bravais lattice, named after , is an infinite array of discrete points generated by a set of discrete translation operations described in three dimensional space by
: \mathbf = n_1 \mathbf_1 + n_2 \mathbf_2 ...
points, is the Landé -factor, is the Bohr magneton
In atomic physics, the Bohr magneton (symbol ) is a physical constant and the natural unit for expressing the magnetic moment of an electron caused by its orbital or spin angular momentum.
In SI units, the Bohr magneton is defined as
\mu_\mat ...
and is the internal field which includes the external field plus any "molecular" field. Note that in the classical continuum case and in dimensions the Heisenberg ferromagnet equation has the form
:
In and dimensions this equation admits several integrable and non-integrable extensions like the Landau-Lifshitz equation, the Ishimori equation The Ishimori equation is a partial differential equation proposed by the Japanese mathematician . Its interest is as the first example of a nonlinear spin-one field model in the plane that is integrable .
Equation
The Ishimori equation has the for ...
and so on. For a ferromagnet and the ground state of the Hamiltonian is that in which all spins are aligned parallel with the field . That is an eigenstate of can be verified by rewriting it in terms of the spin-raising and spin-lowering operators given by:
:
resulting in
:
where has been taken as the direction of the magnetic field. The spin-lowering operator annihilates the state with minimum projection of spin along the -axis, while the spin-raising operator annihilates the ground state with maximum spin projection along the -axis. Since
:
for the maximally aligned state, we find
:
where N is the total number of Bravais lattice sites. The proposition that the ground state is an eigenstate of the Hamiltonian is confirmed.
One might guess that the first excited state of the Hamiltonian has one randomly selected spin at position rotated so that
:
but in fact this arrangement of spins is not an eigenstate. The reason is that such a state is transformed by the spin raising and lowering operators. The operator will increase the -projection of the spin at position back to its low-energy orientation, but the operator will lower the -projection of the spin at position . The combined effect of the two operators is therefore to propagate the rotated spin to a new position, which is a hint that the correct eigenstate is a spin wave, namely a superposition of states with one reduced spin. The exchange energy penalty associated with changing the orientation of one spin is reduced by spreading the disturbance over a long wavelength. The degree of misorientation of any two near-neighbor spins is thereby minimized. From this explanation one can see why the Ising model
The Ising model (or Lenz–Ising model), named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical models in physics, mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that r ...
magnet with discrete symmetry has no spin waves: the notion of spreading a disturbance in the spin lattice over a long wavelength makes no sense when spins have only two possible orientations. The existence of low-energy excitations is related to the fact that in the absence of an external field, the spin system has an infinite number of degenerate ground states with infinitesimally different spin orientations. The existence of these ground states can be seen from the fact that the state does not have the full rotational symmetry of the Hamiltonian , a phenomenon which is called spontaneous symmetry breaking
Spontaneous symmetry breaking is a spontaneous process of symmetry breaking, by which a physical system in a symmetric state spontaneously ends up in an asymmetric state. In particular, it can describe systems where the equations of motion o ...
.
Magnetization
 In this model the magnetization
:
where is the volume. The propagation of spin waves is described by the Landau-Lifshitz equation of motion:
:
where is the gyromagnetic ratio and is the damping constant. The cross-products in this forbidding-looking equation show that the propagation of spin waves is governed by the torques generated by internal and external fields. (An equivalent form is the Landau-Lifshitz-Gilbert equation, which replaces the final term by a more "simple looking" equivalent one.)
The first term on the right hand side of the equation describes the precession of the magnetization under the influence of the applied field, while the above-mentioned final term describes how the magnetization vector "spirals in" towards the field direction as time progresses. In metals the damping forces described by the constant are in many cases dominated by the eddy currents.
One important difference between phonons and magnons lies in their
In this model the magnetization
:
where is the volume. The propagation of spin waves is described by the Landau-Lifshitz equation of motion:
:
where is the gyromagnetic ratio and is the damping constant. The cross-products in this forbidding-looking equation show that the propagation of spin waves is governed by the torques generated by internal and external fields. (An equivalent form is the Landau-Lifshitz-Gilbert equation, which replaces the final term by a more "simple looking" equivalent one.)
The first term on the right hand side of the equation describes the precession of the magnetization under the influence of the applied field, while the above-mentioned final term describes how the magnetization vector "spirals in" towards the field direction as time progresses. In metals the damping forces described by the constant are in many cases dominated by the eddy currents.
One important difference between phonons and magnons lies in their dispersion relation
In the physical sciences and electrical engineering, dispersion relations describe the effect of dispersion on the properties of waves in a medium. A dispersion relation relates the wavelength or wavenumber of a wave to its frequency. Given the ...
s. The dispersion relation for phonons is to first order linear in wavevector , namely , where is frequency, and is the velocity of sound. Magnons have a parabolic dispersion relation: where the parameter represents a " spin stiffness." The form is the third term of a Taylor expansion of a cosine term in the energy expression originating from the dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
. The underlying reason for the difference in dispersion relation is that the order parameter
In physics, chemistry, and other related fields like biology, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic s ...
(magnetization) for the ground-state in ferromagnets violates time-reversal symmetry
T-symmetry or time reversal symmetry is the theoretical symmetry (physics), symmetry of physical laws under the Transformation (mathematics), transformation of time reversal,
: T: t \mapsto -t.
Since the second law of thermodynamics states that ...
. Two adjacent spins in a solid with lattice constant that participate in a mode with wavevector have an angle between them equal to .
Experimental observation
Spin waves are observed through four experimental methods:inelastic neutron scattering
Neutron scattering, the irregular dispersal of free neutrons by matter, can refer to either the naturally occurring physical process itself or to the man-made experimental techniques that use the natural process for investigating materials. Th ...
, inelastic light
Light, visible light, or visible radiation is electromagnetic radiation that can be visual perception, perceived by the human eye. Visible light spans the visible spectrum and is usually defined as having wavelengths in the range of 400– ...
scattering (Brillouin scattering
In electromagnetism, Brillouin scattering (also known as Brillouin light scattering or BLS), named after Léon Brillouin, refers to the interaction of light with the material waves in a medium (e.g. electrostriction and magnetostriction). It is m ...
, Raman scattering
In chemistry and physics, Raman scattering or the Raman effect () is the inelastic scattering of photons by matter, meaning that there is both an exchange of energy and a change in the light's direction. Typically this effect involves vibrationa ...
and inelastic X-ray
An X-ray (also known in many languages as Röntgen radiation) is a form of high-energy electromagnetic radiation with a wavelength shorter than those of ultraviolet rays and longer than those of gamma rays. Roughly, X-rays have a wavelength ran ...
scattering), inelastic electron scattering (spin-resolved electron energy loss spectroscopy), and spin-wave resonance (ferromagnetic resonance
Ferromagnetic resonance, or FMR, is coupling between an electromagnetic wave and the magnetization of a medium through which it passes. This coupling induces a significant loss of power of the wave. The power is absorbed by the precessing magneti ...
).
* In inelastic neutron scattering
Neutron scattering, the irregular dispersal of free neutrons by matter, can refer to either the naturally occurring physical process itself or to the man-made experimental techniques that use the natural process for investigating materials. Th ...
the energy loss of a beam of neutrons that excite a magnon is measured, typically as a function of scattering vector (or equivalently momentum transfer), temperature and external magnetic field. Inelastic neutron scattering measurements can determine the dispersion curve for magnons just as they can for phonon
A phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. In the context of optically trapped objects, the quantized vibration mode can be defined a ...
s. Important inelastic neutron scattering facilities are present at the ISIS neutron source in Oxfordshire, UK, the Institut Laue-Langevin in Grenoble
Grenoble ( ; ; or ; or ) is the Prefectures in France, prefecture and List of communes in France with over 20,000 inhabitants, largest city of the Isère Departments of France, department in the Auvergne-Rhône-Alpes Regions of France, region ...
, France, the High Flux Isotope Reactor at Oak Ridge National Laboratory
Oak Ridge National Laboratory (ORNL) is a federally funded research and development centers, federally funded research and development center in Oak Ridge, Tennessee, United States. Founded in 1943, the laboratory is sponsored by the United Sta ...
in Tennessee, USA, and at the National Institute of Standards and Technology
The National Institute of Standards and Technology (NIST) is an agency of the United States Department of Commerce whose mission is to promote American innovation and industrial competitiveness. NIST's activities are organized into Outline of p ...
in Maryland, USA.
* Brillouin scattering similarly measures the energy loss of photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can ...
s (usually at a convenient visible wavelength) reflected from or transmitted through a magnetic material. Brillouin spectroscopy is similar to the more widely known Raman scattering
In chemistry and physics, Raman scattering or the Raman effect () is the inelastic scattering of photons by matter, meaning that there is both an exchange of energy and a change in the light's direction. Typically this effect involves vibrationa ...
, but probes a lower energy and has a superior energy resolution in order to be able to detect the meV energy of magnons.
* Ferromagnetic (or antiferromagnetic) resonance instead measures the absorption of microwave
Microwave is a form of electromagnetic radiation with wavelengths shorter than other radio waves but longer than infrared waves. Its wavelength ranges from about one meter to one millimeter, corresponding to frequency, frequencies between 300&n ...
s, incident on a magnetic material, by spin waves, typically as a function of angle, temperature and applied field. Ferromagnetic resonance is a convenient laboratory method for determining the effect of magnetocrystalline anisotropy
In physics, a ferromagnetic material is said to have magnetocrystalline anisotropy if it takes more energy to magnetization, magnetize it in certain directions than in others. These directions are usually related to the crystal structure, principa ...
on the dispersion of spin waves. One group at the Max Planck Institute of Microstructure Physics
The Max Planck Institute of Microstructure Physics in Halle (Saale) is a research institute in Germany focused novel materials with useful functionalities. Active research topics includes spintronics, neuromorphic systems, nano-photonics, topologic ...
in Halle, Germany proved that by using spin polarized electron energy loss spectroscopy (SPEELS), very high energy surface magnons can be excited. This technique allows one to probe the dispersion of magnons in the ultrathin ferromagnetic films. The first experiment was performed for a 5 ML Fe film. With momentum resolution, the magnon dispersion was explored for an 8 ML fcc Co film on Cu(001) and an 8 ML hcp Co on W(110), respectively. The maximum magnon energy at the border of the surface Brillouin zone was 240 meV.
Practical significance
When magnetoelectronic devices are operated at high frequencies, the generation of spin waves can be an important energy loss mechanism. Spin wave generation limits the linewidths and therefore thequality factor
In physics and engineering, the quality factor or factor is a dimensionless parameter that describes how underdamped an oscillator or resonator is. It is defined as the ratio of the initial energy stored in the resonator to the energy lost in ...
s ''Q'' of ferrite components used in microwave
Microwave is a form of electromagnetic radiation with wavelengths shorter than other radio waves but longer than infrared waves. Its wavelength ranges from about one meter to one millimeter, corresponding to frequency, frequencies between 300&n ...
devices. The reciprocal of the lowest frequency of the characteristic spin waves of a magnetic material gives a time scale for the switching of a device based on that material.
See also
* Magnonics * Holstein–Primakoff transformation * Spin engineeringReferences
* * * * {{RefendExternal links
Spin waves - The Feynman Lectures on Physics
performing Brillouin scattering measurements. Magnetic ordering Waves de:Spinwelle pl:Fale spinowe