|
Heisenberg Model (quantum)
The quantum Heisenberg model, developed by Werner Heisenberg, is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spins of the magnetic systems are treated quantum mechanically. It is related to the prototypical Ising model, where at each site of a lattice, a spin \sigma_i \in \ represents a microscopic magnetic dipole to which the magnetic moment is either up or down. Except the coupling between magnetic dipole moments, there is also a multipolar version of Heisenberg model called the multipolar exchange interaction. Overview For quantum mechanical reasons (see exchange interaction or ), the dominant coupling between two dipoles may cause nearest-neighbors to have lowest energy when they are ''aligned''. Under this assumption (so that magnetic interactions only occur between adjacent dipoles) and on a 1-dimensional periodic lattice, the Hamiltonian can be written in the form :\hat H = -J \sum_^ \sig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Werner Heisenberg
Werner Karl Heisenberg () (5 December 1901 – 1 February 1976) was a German theoretical physicist and one of the main pioneers of the theory of quantum mechanics. He published his work in 1925 in a breakthrough paper. In the subsequent series of papers with Max Born and Pascual Jordan, during the same year, his matrix formulation of quantum mechanics was substantially elaborated. He is known for the uncertainty principle, which he published in 1927. Heisenberg was awarded the 1932 Nobel Prize in Physics "for the creation of quantum mechanics". Heisenberg also made contributions to the theories of the hydrodynamics of turbulent flows, the atomic nucleus, ferromagnetism, cosmic rays, and subatomic particles. He was a principal scientist in the German nuclear weapons program during World War II. He was also instrumental in planning the first West German nuclear reactor at Karlsruhe, together with a research reactor in Munich, in 1957. Following World War II, he was appointed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partition Function (statistical Mechanics)
In physics, a partition function describes the statistical properties of a system in thermodynamic equilibrium. Partition functions are functions of the thermodynamic state variables, such as the temperature and volume. Most of the aggregate thermodynamic variables of the system, such as the total energy, free energy, entropy, and pressure, can be expressed in terms of the partition function or its derivatives. The partition function is dimensionless. Each partition function is constructed to represent a particular statistical ensemble (which, in turn, corresponds to a particular free energy). The most common statistical ensembles have named partition functions. The canonical partition function applies to a canonical ensemble, in which the system is allowed to exchange heat with the environment at fixed temperature, volume, and number of particles. The grand canonical partition function applies to a grand canonical ensemble, in which the system can exchange both heat and p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ice-type Model
In statistical mechanics, the ice-type models or six-vertex models are a family of vertex models for crystal lattices with hydrogen bonds. The first such model was introduced by Linus Pauling in 1935 to account for the residual entropy of water ice. Variants have been proposed as models of certain ferroelectric and antiferroelectric crystals. In 1967, Elliott H. Lieb found the exact solution to a two-dimensional ice model known as "square ice". The exact solution in three dimensions is only known for a special "frozen" state. Description An ice-type model is a lattice model defined on a lattice of coordination number 4. That is, each vertex of the lattice is connected by an edge to four "nearest neighbours". A state of the model consists of an arrow on each edge of the lattice, such that the number of arrows pointing inwards at each vertex is 2. This restriction on the arrow configurations is known as the ice rule. In graph theoretic terms, the states are Eulerian orientatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
DMRG Of The Heisenberg Model
Within the study of the quantum many-body problem in physics, the DMRG analysis of the Heisenberg model is an important theoretical example applying techniques of the density matrix renormalization group (DMRG) to the Heisenberg model of a chain of spins. This article presents the "infinite" DMRG algorithm for the S=1 antiferromagnetic Heisenberg chain, but the recipe can be applied for every translationally invariant one-dimensional lattice. DMRG is a renormalization-group technique because it offers an efficient truncation of the Hilbert space of one-dimensional quantum systems. The algorithm The Starting Point To simulate an infinite chain, starting with four sites. The first is the ''block site'', the last the ''universe-block site'' and the remaining are the ''added sites'', the right one is added to the universe-block site and the other to the block site. The Hilbert space for the single site is \mathfrak with the base \\equiv\. With this base the spin operators are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
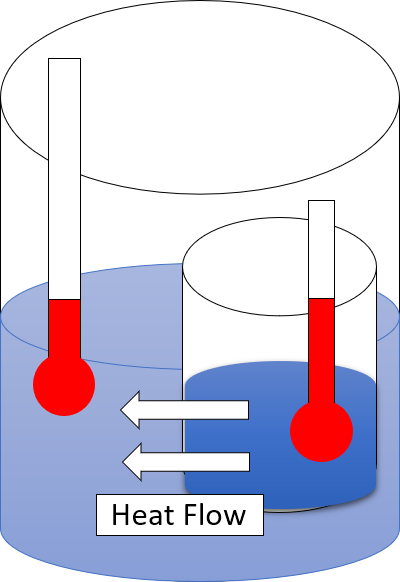
Second Law Of Thermodynamics
The second law of thermodynamics is a physical law based on universal experience concerning heat and Energy transformation, energy interconversions. One simple statement of the law is that heat always moves from hotter objects to colder objects (or "downhill"), unless energy in some form is supplied to reverse the direction of heat flow. Another definition is: "Not all heat energy can be converted into Work (thermodynamics), work in a cyclic process."Young, H. D; Freedman, R. A. (2004). ''University Physics'', 11th edition. Pearson. p. 764. The second law of thermodynamics in other versions establishes the concept of entropy as a physical property of a thermodynamic system. It can be used to predict whether processes are forbidden despite obeying the requirement of conservation of energy as expressed in the first law of thermodynamics and provides necessary criteria for spontaneous processes. The second law may be formulated by the observation that the entropy of isolated systems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy Of Entanglement
The entropy of entanglement (or entanglement entropy) is a measure of the degree of quantum entanglement between two subsystems constituting a two-part composite quantum system. Given a pure bipartite quantum state of the composite system, it is possible to obtain a reduced density matrix describing knowledge of the state of a subsystem. The entropy of entanglement is the Von Neumann entropy of the reduced density matrix for any of the subsystems. If it is non-zero, i.e. the subsystem is in a mixed state, it indicates the two subsystems are entangled. More mathematically; if a state describing two subsystems ''A'' and ''B'' , \Psi_\rangle=, \phi_A\rangle, \phi_B\rangleis a separable state, then the reduced density matrix \rho_A=\operatorname_B, \Psi_\rangle\langle\Psi_, =, \phi_A\rangle\langle\phi_A, is a pure state. Thus, the entropy of the state is zero. Similarly, the density matrix of ''B'' would also have 0 entropy. A reduced density matrix having a non-zero entropy is there ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Short-range Order
In physics, the terms order and disorder designate the presence or absence of some symmetry or correlation in a many-particle system. In condensed matter physics, systems typically are ordered at low temperatures; upon heating, they undergo one or several phase transitions into less ordered states. Examples for such an order-disorder transition are: * the melting of ice: solid-liquid transition, loss of crystalline order; * the demagnetization of iron by heating above the Curie temperature: ferromagnetic-paramagnetic transition, loss of magnetic order. The degree of freedom that is ordered or disordered can be translational (crystalline ordering), rotational (ferroelectric ordering), or a spin state ( magnetic ordering). The order can consist either in a full crystalline space group symmetry, or in a correlation. Depending on how the correlations decay with distance, one speaks of long range order or short range order. If a disordered state is not in thermodynamic equilibriu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiferromagnetism
In materials that exhibit antiferromagnetism, the magnetic moments of atoms or molecules, usually related to the spins of electrons, align in a regular pattern with neighboring spins (on different sublattices) pointing in opposite directions. This is, like ferromagnetism and ferrimagnetism, a manifestation of ordered magnetism. The phenomenon of antiferromagnetism was first introduced by Lev Landau in 1933. Generally, antiferromagnetic order may exist at sufficiently low temperatures, but vanishes at and above the Néel temperature – named after Louis Néel, who had first identified this type of magnetic ordering. Above the Néel temperature, the material is typically paramagnetic. Measurement When no external field is applied, the antiferromagnetic structure corresponds to a vanishing total magnetization. In an external magnetic field, a kind of ferrimagnetic behavior may be displayed in the antiferromagnetic phase, with the absolute value of one of the sublattice magneti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ferromagnetism
Ferromagnetism is a property of certain materials (such as iron) which results in a large observed magnetic permeability, and in many cases a large magnetic coercivity allowing the material to form a permanent magnet. Ferromagnetic materials are the familiar metals noticeably attracted to a magnet, a consequence of their large magnetic permeability. Magnetic permeability describes the induced magnetization of a material due to the presence of an ''external'' magnetic field, and it is this temporarily induced magnetization inside a steel plate, for instance, which accounts for its attraction to the permanent magnet. Whether or not that steel plate acquires a permanent magnetization itself, depends not only on the strength of the applied field, but on the so-called coercivity of that material, which varies greatly among ferromagnetic materials. In physics, several different types of material magnetism are distinguished. Ferromagnetism (along with the similar effect ferrimagnetis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Quantum Group
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity e, a number ranging from e = 0 (the limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but only approximations for its perimeter (also known as circumference), for which integration is required to obtain an exact solution. Analytically, the equation of a standard ellipse centered at the origin with width 2a and height 2b is: : \frac+\frac = 1 . Assuming a \ge b, the foci are (\pm c, 0) for c = \sqrt. The standard parametric equation is: : (x,y) = (a\cos(t),b\sin(t)) \quad \text \quad 0\leq t\leq 2\pi. Ellipses are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Affine Algebras
In mathematics, a quantum affine algebra (or affine quantum group) is a Hopf algebra that is a ''q''-deformation of the universal enveloping algebra of an affine Lie algebra. They were introduced independently by and as a special case of their general construction of a quantum group from a Cartan matrix. One of their principal applications has been to the theory of solvable lattice models in quantum statistical mechanics, where the Yang–Baxter equation occurs with a spectral parameter. Combinatorial aspects of the representation theory of quantum affine algebras can be described simply using crystal bases, which correspond to the degenerate case when the deformation parameter ''q'' vanishes and the Hamiltonian of the associated lattice model can be explicitly diagonalized. See also *Quantum enveloping algebra *Quantum KZ equations In mathematical physics, the quantum KZ equations or quantum Knizhnik–Zamolodchikov equations or qKZ equations are the analogue for quantum aff ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |