|
Spin Connection
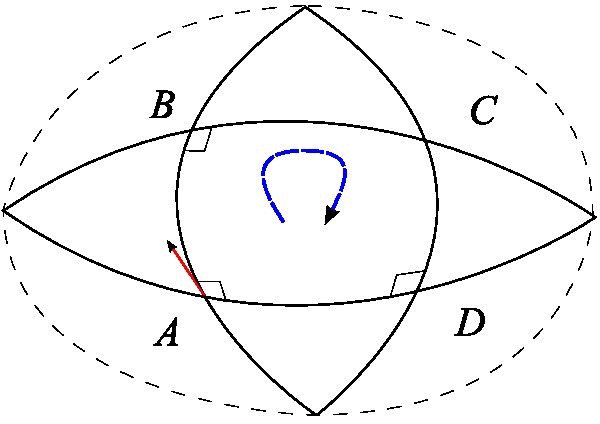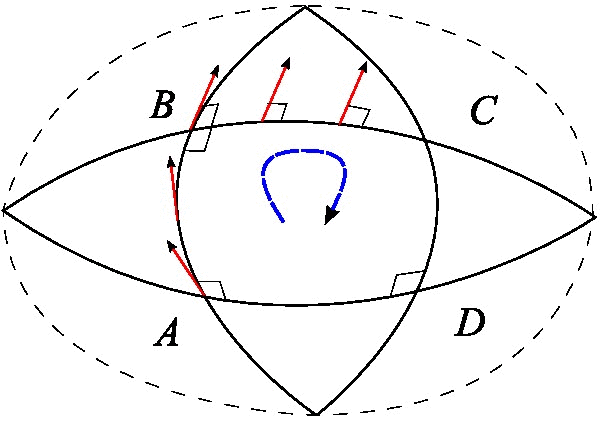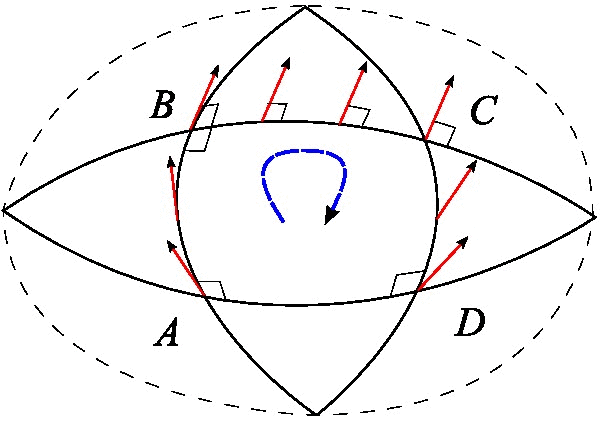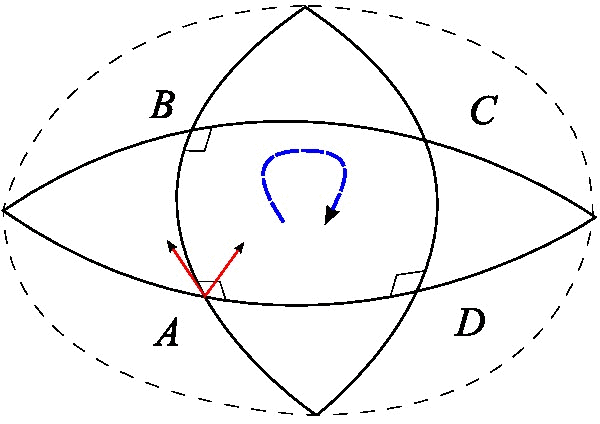
In differential geometry and mathematical physics, a spin connection is a connection on a spinor bundle. It is induced, in a canonical manner, from the affine connection. It can also be regarded as the gauge field generated by local Lorentz transformations. In some canonical formulations of general relativity, a spin connection is defined on spatial slices and can also be regarded as the gauge field generated by local rotations. The spin connection occurs in two common forms: the ''Levi-Civita spin connection'', when it is derived from the Levi-Civita connection, and the ''affine spin connection'', when it is obtained from the affine connection. The difference between the two of these is that the Levi-Civita connection is by definition the unique torsion-free connection, whereas the affine connection (and so the affine spin connection) may contain torsion. Definition Let e_\mu^ be the local Lorentz frame fields or vierbein (also known as a tetrad), which is a set of orthonor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Geometry
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries. Since the late 19th century, differential geometry has grown into a field concerned more generally with geometric structures on differentiable manifolds. A geometric structure is one which defines some notion of size, distance, shape, volume, or other rigidifying structu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curvature Form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. The Riemann curvature tensor in Riemannian geometry can be considered as a special case. Definition Let ''G'' be a Lie group with Lie algebra \mathfrak g, and ''P'' → ''B'' be a principal ''G''-bundle. Let ω be an Ehresmann connection on ''P'' (which is a \mathfrak g-valued one-form on ''P''). Then the curvature form is the \mathfrak g-valued 2-form on ''P'' defined by :\Omega=d\omega + omega \wedge \omega= D \omega. (In another convention, 1/2 does not appear.) Here d stands for exterior derivative, cdot \wedge \cdot/math> is defined in the article "Lie algebra-valued form" and ''D'' denotes the exterior covariant derivative. In other terms, :\,\Omega(X, Y)= d\omega(X,Y) + omega(X),\omega(Y)/math> where ''X'', ''Y'' are tangent vectors to ''P''. There is also another expression for Ω: if ''X'', ''Y'' are horizontal vector fields on ''P'', thenProof: \sigma\Omega(X ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstein–Cartan Theory
In theoretical physics, the Einstein–Cartan theory, also known as the Einstein–Cartan–Sciama–Kibble theory, is a classical theory of gravitation similar to general relativity. The theory was first proposed by Élie Cartan in 1922. Einstein–Cartan theory is the simplest Poincaré gauge theory. Overview Einstein–Cartan theory differs from general relativity in two ways: (1) it is formulated within the framework of Riemann–Cartan geometry, which possesses a locally gauged Lorentz symmetry, while general relativity is formulated within the framework of Riemannian geometry, which does not; (2) an additional set of equations are posed that relate torsion to spin. This difference can be factored into by first reformulating general relativity onto a Riemann–Cartan geometry, replacing the Einstein–Hilbert action over Riemannian geometry by the Palatini action over Riemann–Cartan geometry; and second, removing the zero torsion constraint from the Palatini action, whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Teleparallelism
Teleparallelism (also called teleparallel gravity), was an attempt by Albert Einstein to base a unified theory of electromagnetism and gravity on the mathematical structure of distant parallelism, also referred to as absolute or teleparallelism. In this theory, a spacetime is characterized by a curvature-free linear connection in conjunction with a metric tensor field, both defined in terms of a dynamical tetrad field. Teleparallel spacetimes The crucial new idea, for Einstein, was the introduction of a tetrad field, i.e., a set of four vector fields defined on ''all'' of such that for every the set is a basis of , where denotes the fiber over of the tangent vector bundle . Hence, the four-dimensional spacetime manifold must be a parallelizable manifold. The tetrad field was introduced to allow the distant comparison of the direction of tangent vectors at different points of the manifold, hence the name distant parallelism. His attempt failed because there was no Schwarzs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contorsion Tensor
The contorsion tensor in differential geometry is the difference between a connection with and without torsion in it. It commonly appears in the study of spin connections. Thus, for example, a vielbein together with a spin connection, when subject to the condition of vanishing torsion, gives a description of Einstein gravity. For supersymmetry, the same constraint, of vanishing torsion, gives (the field equations of) 11-dimensional supergravity. That is, the contorsion tensor, along with the connection, becomes one of the dynamical objects of the theory, demoting the metric to a secondary, derived role. The elimination of torsion in a connection is referred to as the ''absorption of torsion'', and is one of the steps of Cartan's equivalence method for establishing the equivalence of geometric structures. Definition in metric geometry In metric geometry, the contorsion tensor expresses the difference between a metric-compatible affine connection with Christoffel symbol \Gamma_^k ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bianchi Identities
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. The Riemann curvature tensor in Riemannian geometry can be considered as a special case. Definition Let ''G'' be a Lie group with Lie algebra \mathfrak g, and ''P'' → ''B'' be a principal ''G''-bundle. Let ω be an Ehresmann connection on ''P'' (which is a \mathfrak g-valued one-form on ''P''). Then the curvature form is the \mathfrak g-valued 2-form on ''P'' defined by :\Omega=d\omega + omega \wedge \omega= D \omega. (In another convention, 1/2 does not appear.) Here d stands for exterior derivative, cdot \wedge \cdot/math> is defined in the article "Lie algebra-valued form" and ''D'' denotes the exterior covariant derivative. In other terms, :\,\Omega(X, Y)= d\omega(X,Y) + omega(X),\omega(Y)/math> where ''X'', ''Y'' are tangent vectors to ''P''. There is also another expression for Ω: if ''X'', ''Y'' are horizontal vector fields on ''P'', thenProof: \sigma\Omega(X ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Curvature Tensor
In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno Christoffel) is the most common way used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold (i.e., it is a tensor field). It is a local invariant of Riemannian metrics which measures the failure of the second covariant derivatives to commute. A Riemannian manifold has zero curvature if and only if it is ''flat'', i.e. locally isometric to the Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection. It is a central mathematical tool in the theory of general relativity, the modern theory of gravity, and the curvature of spacetime is in principle observable via the geodesic deviation equation. The curvature tensor represents the tidal force experienced by a rigid body moving al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cotangent Bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold. It may be described also as the dual bundle to the tangent bundle. This may be generalized to categories with more structure than smooth manifolds, such as complex manifolds, or (in the form of cotangent sheaf) algebraic varieties or schemes. In the smooth case, any Riemannian metric or symplectic form gives an isomorphism between the cotangent bundle and the tangent bundle, but they are not in general isomorphic in other categories. Formal Definition Let ''M'' be a smooth manifold and let ''M''×''M'' be the Cartesian product of ''M'' with itself. The diagonal mapping Δ sends a point ''p'' in ''M'' to the point (''p'',''p'') of ''M''×''M''. The image of Δ is called the diagonal. Let \mathcal be the sheaf of germs of smooth functions on ''M''×''M'' which vanish on the diagona ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Group
In mathematics, a Lie group (pronounced ) is a group that is also a differentiable manifold. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additional properties it must have to be thought of as a "transformation" in the abstract sense, for instance multiplication and the taking of inverses (division), or equivalently, the concept of addition and the taking of inverses (subtraction). Combining these two ideas, one obtains a continuous group where multiplying points and their inverses are continuous. If the multiplication and taking of inverses are smooth (differentiable) as well, one obtains a Lie group. Lie groups provide a natural model for the concept of continuous symmetry, a celebrated example of which is the rotational symmetry in three dimensions (given by the special orthogonal group \text(3)). Lie groups are widely used in many parts of modern mathematics and physics. Lie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gauge Theory
In physics, a gauge theory is a type of field theory in which the Lagrangian (and hence the dynamics of the system itself) does not change (is invariant) under local transformations according to certain smooth families of operations (Lie groups). The term ''gauge'' refers to any specific mathematical formalism to regulate redundant degrees of freedom in the Lagrangian of a physical system. The transformations between possible gauges, called ''gauge transformations'', form a Lie group—referred to as the ''symmetry group'' or the ''gauge group'' of the theory. Associated with any Lie group is the Lie algebra of group generators. For each group generator there necessarily arises a corresponding field (usually a vector field) called the ''gauge field''. Gauge fields are included in the Lagrangian to ensure its invariance under the local group transformations (called ''gauge invariance''). When such a theory is quantized, the quanta of the gauge fields are called '' gauge bosons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemannian Geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a ''Riemannian metric'', i.e. with an inner product on the tangent space at each point that varies smoothly from point to point. This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions. Riemannian geometry originated with the vision of Bernhard Riemann expressed in his inaugural lecture "''Ueber die Hypothesen, welche der Geometrie zu Grunde liegen''" ("On the Hypotheses on which Geometry is Based.") It is a very broad and abstract generalization of the differential geometry of surfaces in R3. Development of Riemannian geometry resulted in synthesis of diverse results concerning the geometry of surfaces and the behavior of geodesics on them, with techniques that can be applied to the study of differentiable manifolds of higher dim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |