|
Sphere Wrapped Round Itself
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is the sphe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
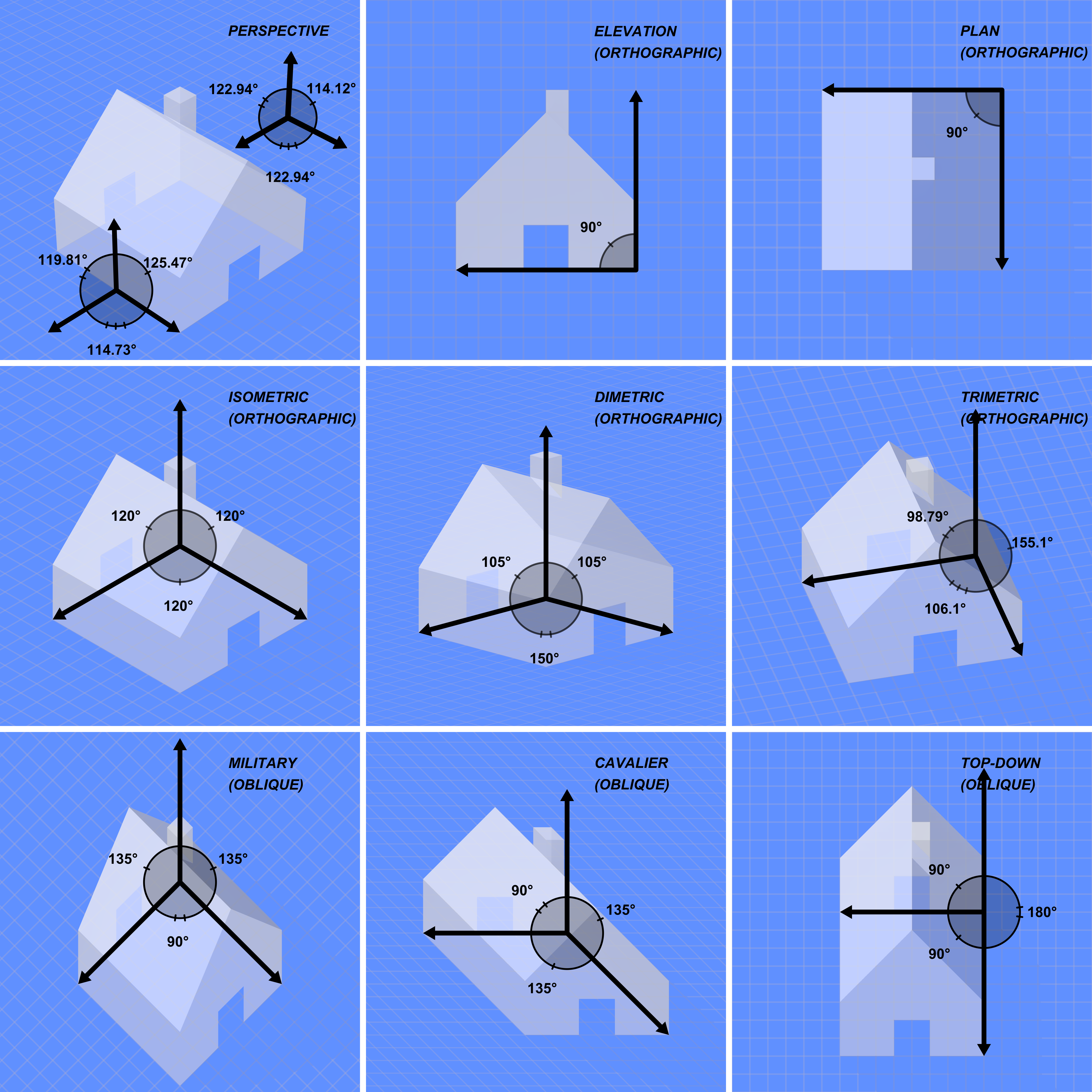
3D Projection
A 3D projection (or graphical projection) is a design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane. 3D projections use the primary qualities of an object's basic shape to create a map of points, that are then connected to one another to create a visual element. The result is a graphic that contains conceptual properties to interpret that the figure or image as not actually flat (2D), but rather, as a solid object (3D) being viewed on a 2D display. 3D objects are largely displayed on two-dimensional mediums (i.e. paper and computer monitors). As such, graphical projections are a commonly used design element; notably, in engineering drawing, drafting, and computer graphics. Projections can be calculated through employment of mathematical analysis and formulae, or by using various geometric and op ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pressure Vessels
A pressure vessel is a container designed to hold gases or liquids at a pressure substantially different from the ambient pressure. Construction methods and materials may be chosen to suit the pressure application, and will depend on the size of the vessel, the contents, working pressure, mass constraints, and the number of items required. Pressure vessels can be dangerous, and fatal accidents have occurred in the history of their development and operation. Consequently, pressure vessel design, manufacture, and operation are regulated by engineering authorities backed by legislation. For these reasons, the definition of a pressure vessel varies from country to country. Design involves parameters such as maximum safe operating pressure and temperature, safety factor, corrosion allowance and minimum design temperature (for brittle fracture). Construction is tested using nondestructive testing, such as ultrasonic testing, radiography, and pressure tests. Hydrostatic pressure te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Longitude
Longitude (, ) is a geographic coordinate that specifies the east– west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek letter lambda (λ). Meridians are semicircular lines running from pole to pole that connect points with the same longitude. The prime meridian defines 0° longitude; by convention the International Reference Meridian for the Earth passes near the Royal Observatory in Greenwich, England on the island of Great Britain. Positive longitudes are east of the prime meridian, and negative ones are west. Because of the Earth's rotation, there is a close connection between longitude and time measurement. Scientifically precise local time varies with longitude: a difference of 15° longitude corresponds to a one-hour difference in local time, due to the differing position in relation to the Sun. Comparing local time to an absolute measure of ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equator
The equator is a circle of latitude, about in circumference, that divides Earth into the Northern and Southern hemispheres. It is an imaginary line located at 0 degrees latitude, halfway between the North and South poles. The term can also be used for any other celestial body that is roughly spherical. In spatial (3D) geometry, as applied in astronomy, the equator of a rotating spheroid (such as a planet) is the parallel (circle of latitude) at which latitude is defined to be 0°. It is an imaginary line on the spheroid, equidistant from its poles, dividing it into northern and southern hemispheres. In other words, it is the intersection of the spheroid with the plane perpendicular to its axis of rotation and midway between its geographical poles. On and near the equator (on Earth), noontime sunlight appears almost directly overhead (no more than about 23° from the zenith) every day, year-round. Consequently, the equator has a rather stable daytime temperature ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earth
Earth is the third planet from the Sun and the only astronomical object known to harbor life. While large volumes of water can be found throughout the Solar System, only Earth sustains liquid surface water. About 71% of Earth's surface is made up of the ocean, dwarfing Earth's polar ice, lakes, and rivers. The remaining 29% of Earth's surface is land, consisting of continents and islands. Earth's surface layer is formed of several slowly moving tectonic plates, which interact to produce mountain ranges, volcanoes, and earthquakes. Earth's liquid outer core generates the magnetic field that shapes the magnetosphere of the Earth, deflecting destructive solar winds. The atmosphere of the Earth consists mostly of nitrogen and oxygen. Greenhouse gases in the atmosphere like carbon dioxide (CO2) trap a part of the energy from the Sun close to the surface. Water vapor is widely present in the atmosphere and forms clouds that cover most of the planet. More sola ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point. Any arc of a great circle is a geodesic of the sphere, so that great circles in spherical geometry are the natural analog of straight lines in Euclidean space. For any pair of distinct non- antipodal points on the sphere, there is a unique great circle passing through both. (Every great circle through any point also passes through its antipodal point, so there are infinitely many great circles through two antipodal points.) The shorter of the two great-circle arcs between two distinct points on the sphere is called the ''minor arc'', and is the shortest surface-path between them. Its arc length is the great-circle distance between the points (the intrinsic distance on a sphere), and is proportional to the measure of the central angle formed by the two points and the center of the sphere. A great circle is the largest circle that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Sphere
In mathematics, a unit sphere is simply a sphere of radius one around a given center. More generally, it is the set of points of distance 1 from a fixed central point, where different norms can be used as general notions of "distance". A unit ball is the closed set of points of distance less than or equal to 1 from a fixed central point. Usually the center is at the origin of the space, so one speaks of "the unit ball" or "the unit sphere". Special cases are the unit circle and the unit disk. The importance of the unit sphere is that any sphere can be transformed to a unit sphere by a combination of translation and scaling. In this way the properties of spheres in general can be reduced to the study of the unit sphere. Unit spheres and balls in Euclidean space In Euclidean space of ''n'' dimensions, the -dimensional unit sphere is the set of all points (x_1, \ldots, x_n) which satisfy the equation : x_1^2 + x_2^2 + \cdots + x_n ^2 = 1. The ''n''-dimensional open u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antipodal Point
In mathematics, antipodal points of a sphere are those diametrically opposite to each other (the specific qualities of such a definition are that a line drawn from the one to the other passes through the center of the sphere so forms a true diameter). This term applies to opposite points on a circle or any n-sphere. An antipodal point is sometimes called an antipode, a back-formation from the Greek loan word ''antipodes'', meaning "opposite (the) feet", as the true word singular is ''antipus''. Theory In mathematics, the concept of ''antipodal points'' is generalized to spheres of any dimension: two points on the sphere are antipodal if they are opposite ''through the centre''; for example, taking the centre as origin, they are points with related vectors v and −v. On a circle, such points are also called diametrically opposite. In other words, each line through the centre intersects the sphere in two points, one for each ray out from the centre, and these two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for the diameter of a sphere. In more modern usage, the length d of a diameter is also called the diameter. In this sense one speaks of diameter rather than diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the radius r. :d = 2r \qquad\text\qquad r = \frac. For a convex shape in the plane, the diameter is defined to be the largest distance that can be formed between two opposite parallel lines tangent to its boundary, and the is often defined to be the smallest such distance. Both quantities can be calculated efficiently using rotating calipers. For a curve of constant width such as the Reuleaux triangle, the width and diameter are the same beca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere And Ball
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ball Bearings
A ball bearing is a type of rolling-element bearing that uses balls to maintain the separation between the bearing races. The purpose of a ball bearing is to reduce rotational friction and support radial and axial loads. It achieves this by using at least two races to contain the balls and transmit the loads through the balls. In most applications, one race is stationary and the other is attached to the rotating assembly (e.g., a hub or shaft). As one of the bearing races rotates it causes the balls to rotate as well. Because the balls are rolling they have a much lower coefficient of friction than if two flat surfaces were sliding against each other. Ball bearings tend to have lower load capacity for their size than other kinds of rolling-element bearings due to the smaller contact area between the balls and races. However, they can tolerate some misalignment of the inner and outer races. History Although bearings had been developed since ancient times, the first m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ball
A ball is a round object (usually spherical, but can sometimes be ovoid) with several uses. It is used in ball games, where the play of the game follows the state of the ball as it is hit, kicked or thrown by players. Balls can also be used for simpler activities, such as catch or juggling. Balls made from hard-wearing materials are used in engineering applications to provide very low friction bearings, known as ball bearings. Black-powder weapons use stone and metal balls as projectiles. Although many types of balls are today made from rubber, this form was unknown outside the Americas until after the voyages of Columbus. The Spanish were the first Europeans to see the bouncing rubber balls (although solid and not inflated) which were employed most notably in the Mesoamerican ballgame. Balls used in various sports in other parts of the world prior to Columbus were made from other materials such as animal bladders or skins, stuffed with various materials. As balls are o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |