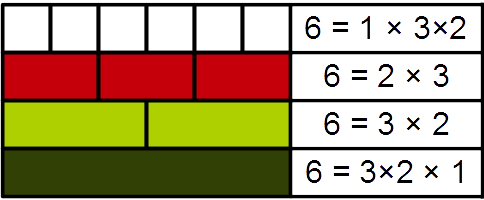
|
Sphenic Number
In number theory, a sphenic number (from grc, σφήνα, 'wedge') is a positive integer that is the product of three distinct prime numbers. Because there are infinitely many prime numbers, there are also infinitely many sphenic numbers. Definition A sphenic number is a product ''pqr'' where ''p'', ''q'', and ''r'' are three distinct prime numbers. In other words, the sphenic numbers are the square-free 3-almost primes. Examples The smallest sphenic number is 30 = 2 × 3 × 5, the product of the smallest three primes. The first few sphenic numbers are : 30, 42, 66, 70, 78, 102, 105, 110, 114, 130, 138, 154, 165, ... the largest known sphenic number is :(282,589,933 − 1) × (277,232,917 − 1) × (274,207,281 − 1). It is the product of the three largest known primes. Divisors All sphenic numbers have exactly eight divisors. If we express the sphenic number as n = p \cdot q \cdot r, where ''p'', ''q'', and ''r'' are distinct primes, then the set of divisors of ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics."German original: "Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik." Number theorists study prime numbers as well as the properties of mathematical objects made out of integers (for example, rational numbers) or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of Complex analysis, analytical objects (for example, the Riemann zeta function) that encode properties of the integers, primes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
114 (number)
114 (one hundred ndfourteen) is the natural number following 113 and preceding 115. In mathematics *114 is an abundant number, a sphenic number and a Harshad number. It is the sum of the first four hyperfactorials, including H(0). At 114, the Mertens function sets a new low of -6, a record that stands until 197. *114 is the smallest positive integer* which has yet to be represented as a3 + b3 + c3, where a, b, and c are integers. It is conjectured that 114 can be represented this way. (*Excluding integers of the form 9k ± 4, for which solutions are known not to exist.) *There is no answer to the equation φ(x) = 114, making 114 a nontotient. *114 appears in the Padovan sequence, preceded by the terms 49, 65, 86 (it is the sum of the first two of these). *114 is a repdigit In recreational mathematics, a repdigit or sometimes monodigit is a natural number composed of repeated instances of the same digit in a positional number system (often implicitly decimal). The word is a po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Almost Prime
In number theory, a natural number is called ''k''-almost prime if it has ''k'' prime factors. More formally, a number ''n'' is ''k''-almost prime if and only if Ω(''n'') = ''k'', where Ω(''n'') is the total number of primes in the prime factorization of ''n'' (can be also seen as the sum of all the primes' exponents): :\Omega(n) := \sum a_i \qquad\mbox\qquad n = \prod p_i^. A natural number is thus prime if and only if it is 1-almost prime, and semiprime if and only if it is 2-almost prime. The set of ''k''-almost primes is usually denoted by ''P''''k''. The smallest ''k''-almost prime is 2''k''. The first few ''k''-almost primes are: : The number π''k''(''n'') of positive integers less than or equal to ''n'' with exactly ''k'' prime divisors (not necessarily distinct) is asymptotic to: : \pi_k(n) \sim \left( \frac \right) \frac, a result of Landau. See also the Hardy–Ramanujan theorem In mathematics, the Hardy–Ramanujan theorem, proved by , states that the nor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semiprime
In mathematics, a semiprime is a natural number that is the product of exactly two prime numbers. The two primes in the product may equal each other, so the semiprimes include the squares of prime numbers. Because there are infinitely many prime numbers, there are also infinitely many semiprimes. Semiprimes are also called biprimes. Examples and variations The semiprimes less than 100 are: Semiprimes that are not square numbers are called discrete, distinct, or squarefree semiprimes: The semiprimes are the case k=2 of the k-almost primes, numbers with exactly k prime factors. However some sources use "semiprime" to refer to a larger set of numbers, the numbers with at most two prime factors (including unit (1), primes, and semiprimes). These are: Formula for number of semiprimes A semiprime counting formula was discovered by E. Noel and G. Panos in 2005. Let \pi_2(n) denote the number of semiprimes less than or equal to n. Then \pi_2(n) = \sum_^ pi(n/p_k) - k + 1 /math> where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclotomic Polynomials
In mathematics, the ''n''th cyclotomic polynomial, for any positive integer ''n'', is the unique irreducible polynomial with integer coefficients that is a divisor of x^n-1 and is not a divisor of x^k-1 for any Its roots are all ''n''th primitive roots of unity e^ , where ''k'' runs over the positive integers not greater than ''n'' and coprime to ''n'' (and ''i'' is the imaginary unit). In other words, the ''n''th cyclotomic polynomial is equal to : \Phi_n(x) = \prod_\stackrel \left(x-e^\right). It may also be defined as the monic polynomial with integer coefficients that is the minimal polynomial over the field of the rational numbers of any primitive ''n''th-root of unity ( e^ is an example of such a root). An important relation linking cyclotomic polynomials and primitive roots of unity is :\prod_\Phi_d(x) = x^n - 1, showing that is a root of x^n - 1 if and only if it is a ''d''th primitive root of unity for some ''d'' that divides ''n''. Examples If ''n'' is a prime ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Möbius Function
The Möbius function is a multiplicative function in number theory introduced by the German mathematician August Ferdinand Möbius (also transliterated ''Moebius'') in 1832. It is ubiquitous in elementary and analytic number theory and most often appears as part of its namesake the Möbius inversion formula. Following work of Gian-Carlo Rota in the 1960s, generalizations of the Möbius function were introduced into combinatorics, and are similarly denoted . Definition For any positive integer , define as the sum of the primitive th roots of unity. It has values in depending on the factorization of into prime factors: * if is a square-free positive integer with an even number of prime factors. * if is a square-free positive integer with an odd number of prime factors. * if has a squared prime factor. The Möbius function can alternatively be represented as : \mu(n) = \delta_ \lambda(n), where is the Kronecker delta, is the Liouville function, is the number of dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Largest Known Prime
The largest known prime number () is , a number which has 24,862,048 digits when written in base 10. It was found via a computer volunteered by Patrick Laroche of the Great Internet Mersenne Prime Search (GIMPS) in 2018. A prime number is a positive integer, excluding 1, with no divisors other than 1 and itself. According to Euclid's theorem there are infinitely many prime numbers, so there is no largest prime. Many of the largest known primes are Mersenne primes, numbers that are one less than a power of two, because they can utilise a specialised primality test that is faster than the general one. , the eight largest known primes are Mersenne primes. The last seventeen record primes were Mersenne primes. The binary representation of any Mersenne prime is composed of all 1's, since the binary form of 2''k'' − 1 is simply ''k'' 1's. Current record The record is currently held by with 24,862,048 digits, found by GIMPS in December 2018. The first and last 120 digits of its val ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
165 (number)
165 (one hundred ndsixty-five) is the natural number following 164 and preceding 166. In mathematics 165 is: *an odd number, a composite number, and a deficient number. *a sphenic number. *a tetrahedral number *the sum of the sums of the divisors of the first 14 positive integers. *a self number in base 10. *a palindromic number in binary (101001012) and bases 14 (BB14), 32 (5532) and 54 (3354). *a unique period in base 2. In astronomy * 165 Loreley is a large Main belt asteroid * 165P/LINEAR is a periodic comet in the Solar System In the military * Caproni Ca.165 Italian fighter aircraft developed before World War II * was a United States Navy tanker, part of the U.S. Reserve Fleet, Beaumont, Texas * was a United States Navy ''Barracuda''-class submarine during World War II * was a United States Navy during World War II * was a United States Navy during World War II * USS ''Counsel'' (AM-165) was a United States Navy during World War II * was a United States Navy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
154 (number)
154 (one hundred ndfifty-four) is the natural number following 153 and preceding 155. In mathematics 154 is a nonagonal number. Its factorization makes 154 a sphenic number There is no integer with exactly 154 coprimes below it, making 154 a noncototient, nor is there, in base 10, any integer that added up to its own digits yields 154, making 154 a self number 154 is the sum of the first six factorials, if one starts with 0! and assumes that 0!=1. With just 17 cuts, a pancake can be cut up into 154 pieces (Lazy caterer's sequence). The distinct prime factors of 154 add up to 20, and so do the ones of 153, hence the two form a Ruth-Aaron pair. 154! + 1 is a factorial prime. In music * 154 is an album by Wire, named for the number of live gigs Wire had performed at that time In the military * was a United States Navy ''Trefoil''-class concrete barge during World War II * was a United States Navy ''Admirable''-class minesweeper during World War II * was a United States Na ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
138 (number)
138 (one hundred ndthirty-eight) is the natural number following 137 and preceding 139. In mathematics 138 is a sphenic number, the sum of four consecutive primes (29 + 31 + 37 + 41), and the smallest product of three primes, such that in base 10, the third prime is a concatenation of the other two: 2 \cdot 3 \cdot 23. 138 is the third 47- gonal number and an Ulam number, as well as a one step palindrome (138 + 831 = 969.) 138 is the 72nd normal congruent number and the 49th primitive or square free congruent number. In astronomy * 138 Tolosa is a brightly colored, stony main belt asteroid * The New General Catalogue object NGC-138, a spiral galaxy in the constellation Pisces * The Saros number of the solar eclipse series which began on June 6, 1472 and will end on July 11, 2716. The duration of Saros series 138 is 1244 years, and it contains 70 solar eclipses * 138P/Shoemaker-Levy is a periodic comet in the Solar System In the military * United States Air Force 138th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
130 (number)
130 (one hundred ndthirty) is the natural number following 129 and preceding 131. In mathematics 130 is a sphenic number. It is a noncototient since there is no answer to the equation ''x'' - φ(''x'') = 130. 130 is the only integer that is the sum of the squares of its first four divisors, including 1: 12 + 22 + 52 + 102 = 130. 130 is the largest number that cannot be written as the sum of four hexagonal numbers. 130 equals both 27 + 2 and 53 + 5 and is therefore a ''doubly strictly '' number. In religion The Book of Genesis states Adam had Seth at the age of 130. The Second Book of Chronicles says that Jehoiada died at the age of 130. In other fields One hundred ndthirty is also: * The year AD 130 or 130 BC * The 130 nanometer process is a semiconductor process technology by semiconductor companies * A 130-30 fund or a ratio up to 150/50 is a type of collective investment vehicle * The C130 Hercules aircraft References See also * List of highways numbered 130 * U ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
110 (number)
110 (one hundred ndten) is the natural number following 109 and preceding 111. In mathematics 110 is a sphenic number and a pronic number. Following the prime quadruplet (101, 103, 107, 109), at 110, the Mertens function reaches a low of −5. 110 is the sum of three consecutive squares, 110 = 5^2 + 6^2 + 7^2. RSA-110 is one of the RSA numbers, large semiprimes that are part of the RSA Factoring Challenge. In base 10, the number 110 is a Harshad number and a self number. In science * The atomic number of darmstadtium. In religion * According to the Bible, the figures Joseph and Joshua both died at the age of 110. In sports Olympic male track and field athletics run 110 metre hurdles. (Female athletes run the 100 metre hurdles instead.) The International 110, or the 110, is a one-design racing sailboat designed in 1939 by C. Raymond Hunt. In other fields 110 is also: * The year AD 110 or 110 BC * A common name for mains electricity in North America, despite the nomina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
