|
Significance (statistics)
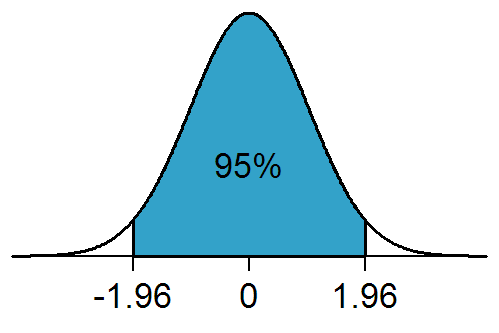
In statistical hypothesis testing, a result has statistical significance when it is very unlikely to have occurred given the null hypothesis (simply by chance alone). More precisely, a study's defined significance level, denoted by \alpha, is the probability of the study rejecting the null hypothesis, given that the null hypothesis is true; and the ''p''-value of a result, ''p'', is the probability of obtaining a result at least as extreme, given that the null hypothesis is true. The result is statistically significant, by the standards of the study, when p \le \alpha. The significance level for a study is chosen before data collection, and is typically set to 5% or much lower—depending on the field of study. In any experiment or observation that involves drawing a sample from a population, there is always the possibility that an observed effect would have occurred due to sampling error alone. But if the ''p''-value of an observed effect is less than (or equal to) the significan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Hypothesis Testing
A statistical hypothesis test is a method of statistical inference used to decide whether the data at hand sufficiently support a particular hypothesis. Hypothesis testing allows us to make probabilistic statements about population parameters. History Early use While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Modern origins and early controversy Modern significance testing is largely the product of Karl Pearson ( ''p''-value, Pearson's chi-squared test), William Sealy Gosset ( Student's t-distribution), and Ronald Fisher ("null hypothesis", analysis of variance, "significance test"), while hypothesis testing was developed by Jerzy Neyman and Egon Pearson (son of Karl). Ronald Fisher began his life in statistics as a Bayesian (Zabell 1992), but Fisher soon grew disenchanted with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
False Positives And False Negatives
A false positive is an error in binary classification in which a test result incorrectly indicates the presence of a condition (such as a disease when the disease is not present), while a false negative is the opposite error, where the test result incorrectly indicates the absence of a condition when it is actually present. These are the two kinds of errors in a binary test, in contrast to the two kinds of correct result (a and a ). They are also known in medicine as a false positive (or false negative) diagnosis, and in statistical classification as a false positive (or false negative) error. In statistical hypothesis testing the analogous concepts are known as type I and type II errors, where a positive result corresponds to rejecting the null hypothesis, and a negative result corresponds to not rejecting the null hypothesis. The terms are often used interchangeably, but there are differences in detail and interpretation due to the differences between medical testing and statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Particle Physics
Particle physics or high energy physics is the study of fundamental particles and forces that constitute matter and radiation. The fundamental particles in the universe are classified in the Standard Model as fermions (matter particles) and bosons (force-carrying particles). There are three generations of fermions, but ordinary matter is made only from the first fermion generation. The first generation consists of up and down quarks which form protons and neutrons, and electrons and electron neutrinos. The three fundamental interactions known to be mediated by bosons are electromagnetism, the weak interaction, and the strong interaction. Quarks cannot exist on their own but form hadrons. Hadrons that contain an odd number of quarks are called baryons and those that contain an even number are called mesons. Two baryons, the proton and the neutron, make up most of the mass of ordinary matter. Mesons are unstable and the longest-lived last for only a few hundredths of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Power
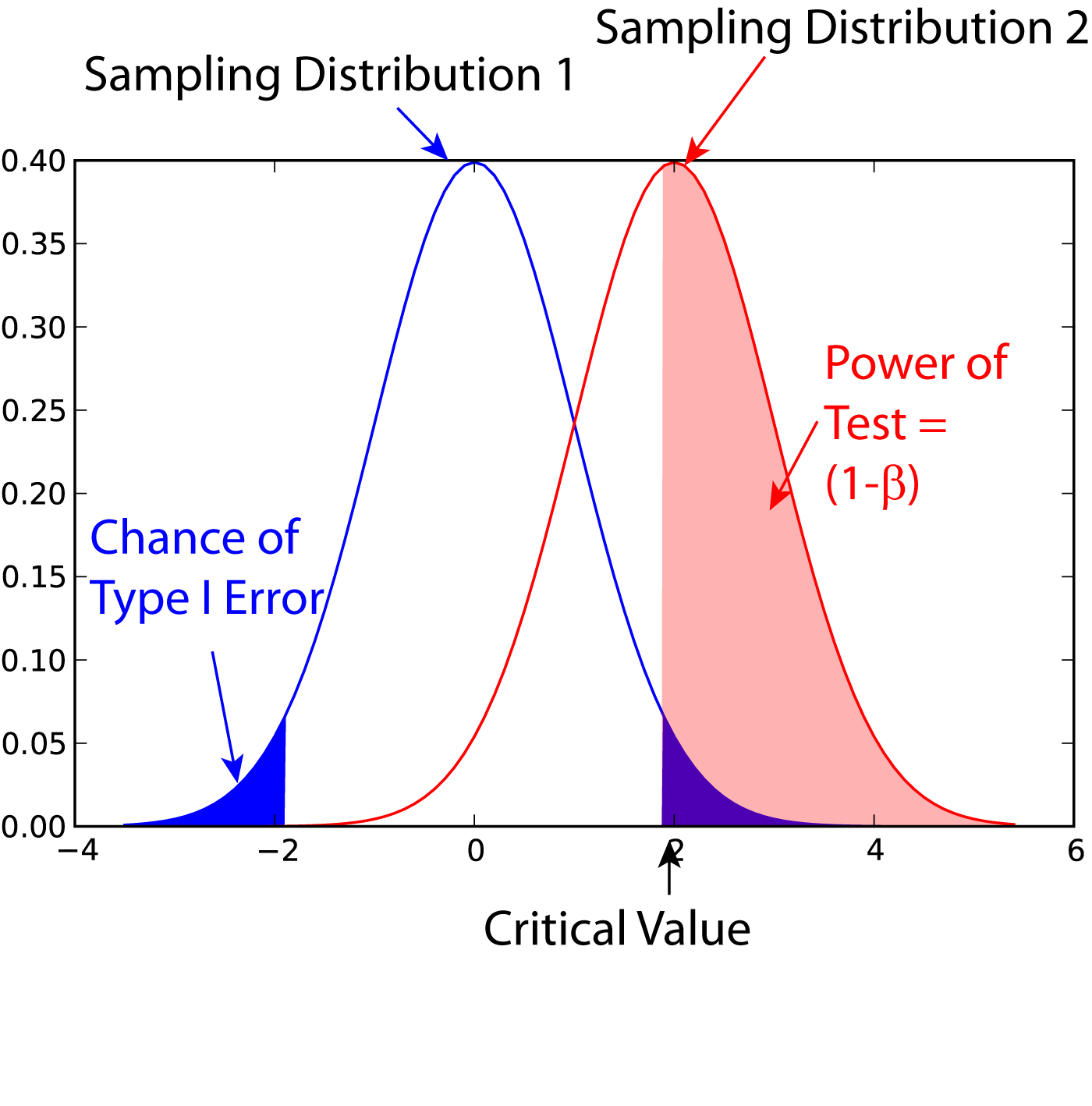
In statistics, the power of a binary hypothesis test is the probability that the test correctly rejects the null hypothesis (H_0) when a specific alternative hypothesis (H_1) is true. It is commonly denoted by 1-\beta, and represents the chances of a true positive detection conditional on the actual existence of an effect to detect. Statistical power ranges from 0 to 1, and as the power of a test increases, the probability \beta of making a type II error by wrongly failing to reject the null hypothesis decreases. Notation This article uses the following notation: * ''β'' = probability of a Type II error, known as a "false negative" * 1 − ''β'' = probability of a "true positive", i.e., correctly rejecting the null hypothesis. "1 − ''β''" is also known as the power of the test. * ''α'' = probability of a Type I error, known as a "false positive" * 1 − ''α'' = probability of a "true negative", i.e., correctly not rejecting the null hypothesis Description For a ty ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternative Hypothesis
In statistical hypothesis testing, the alternative hypothesis is one of the proposed proposition in the hypothesis test. In general the goal of hypothesis test is to demonstrate that in the given condition, there is sufficient evidence supporting the credibility of alternative hypothesis instead of the exclusive proposition in the test (null hypothesis). It is usually consistent with the research hypothesis because it is constructed from literature review, previous studies, etc. However, the research hypothesis is sometimes consistent with the null hypothesis. In statistics, alternative hypothesis is often denoted as Ha or H1. Hypotheses are formulated to compare in a statistical hypothesis test. In the domain of inferential statistics two rival hypotheses can be compared by explanatory power and predictive power. Basic definition The ''alternative hypothesis'' and ''null hypothesis'' are types of conjectures used in statistical tests, which are formal methods of reaching ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Research Question
A research question is "a question that a research project sets out to answer". Choosing a research question is an essential element of both quantitative and qualitative research. Investigation will require data collection and analysis, and the methodology for this will vary widely. Good research questions seek to improve knowledge on an important topic, and are usually narrow and specific. To form a research question, one must determine what type of study will be conducted such as a qualitative, quantitative, or mixed study. Additional factors, such as project funding, may not only affect the research question itself but also when and how it is formed during the research process. Literature suggests several variations on criteria selection for constructing a research question, such as the FINER or PICOT methods. Definition The answer to a research question will help address a research problem or question. Specifying a research question, "the central issue to be resolved by a fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two-tailed Test
In statistical significance testing, a one-tailed test and a two-tailed test are alternative ways of computing the statistical significance of a parameter inferred from a data set, in terms of a test statistic. A two-tailed test is appropriate if the estimated value is greater or less than a certain range of values, for example, whether a test taker may score above or below a specific range of scores. This method is used for null hypothesis testing and if the estimated value exists in the critical areas, the alternative hypothesis is accepted over the null hypothesis. A one-tailed test is appropriate if the estimated value may depart from the reference value in only one direction, left or right, but not both. An example can be whether a machine produces more than one-percent defective products. In this situation, if the estimated value exists in one of the one-sided critical areas, depending on the direction of interest (greater than or less than), the alternative hypothesis is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-tailed Test
In statistical significance testing, a one-tailed test and a two-tailed test are alternative ways of computing the statistical significance of a parameter inferred from a data set, in terms of a test statistic. A two-tailed test is appropriate if the estimated value is greater or less than a certain range of values, for example, whether a test taker may score above or below a specific range of scores. This method is used for null hypothesis testing and if the estimated value exists in the critical areas, the alternative hypothesis is accepted over the null hypothesis. A one-tailed test is appropriate if the estimated value may depart from the reference value in only one direction, left or right, but not both. An example can be whether a machine produces more than one-percent defective products. In this situation, if the estimated value exists in one of the one-sided critical areas, depending on the direction of interest (greater than or less than), the alternative hypothesis is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sampling Distribution
In statistics, a sampling distribution or finite-sample distribution is the probability distribution of a given random-sample-based statistic. If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value of a statistic (such as, for example, the sample mean or sample variance) for each sample, then the sampling distribution is the probability distribution of the values that the statistic takes on. In many contexts, only one sample is observed, but the sampling distribution can be found theoretically. Sampling distributions are important in statistics because they provide a major simplification en route to statistical inference. More specifically, they allow analytical considerations to be based on the probability distribution of a statistic, rather than on the joint probability distribution of all the individual sample values. Introduction The sampling distribution of a statistic is the distri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Probability
In probability theory, conditional probability is a measure of the probability of an event occurring, given that another event (by assumption, presumption, assertion or evidence) has already occurred. This particular method relies on event B occurring with some sort of relationship with another event A. In this event, the event B can be analyzed by a conditional probability with respect to A. If the event of interest is and the event is known or assumed to have occurred, "the conditional probability of given ", or "the probability of under the condition ", is usually written as or occasionally . This can also be understood as the fraction of probability B that intersects with A: P(A \mid B) = \frac. For example, the probability that any given person has a cough on any given day may be only 5%. But if we know or assume that the person is sick, then they are much more likely to be coughing. For example, the conditional probability that someone unwell (sick) is coughing might be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Type I Error
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a "false positive" finding or conclusion; example: "an innocent person is convicted"), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a "false negative" finding or conclusion; example: "a guilty person is not convicted"). Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process. By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased. The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science. Intuitively, type I errors can be thought of as errors of ''commission'', i.e. the researcher unluck ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |