|
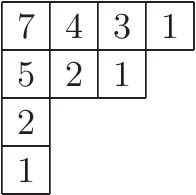
Schur Polynomials
In mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in ''n'' variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of polynomial irreducible representations of the general linear groups. The Schur polynomials form a linear basis for the space of all symmetric polynomials. Any product of Schur polynomials can be written as a linear combination of Schur polynomials with non-negative integral coefficients; the values of these coefficients is given combinatorially by the Littlewood–Richardson rule. More generally, skew Schur polynomials are associated with pairs of partitions and have similar properties to Schur polynomials. Definition (Jacobi's bialternant formula) Schur polynomials are indexed by integer partitions. Given a partition , where , and each is a non-negative integer, the functions a_ ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lindström–Gessel–Viennot Lemma
In Mathematics, the Lindström–Gessel–Viennot lemma provides a way to count the number of tuples of non-intersecting lattice paths, or, more generally, paths on a directed graph. It was proved by Gessel–Viennot in 1985, based on previous work of Lindström published in 1973. Statement Let ''G'' be a locally finite directed acyclic graph. This means that each vertex has finite degree, and that ''G'' contains no directed cycles. Consider base vertices A = \ and destination vertices B = \, and also assign a weight \omega_ to each directed edge ''e''. These edge weights are assumed to belong to some commutative ring. For each directed path ''P'' between two vertices, let \omega(P) be the product of the weights of the edges of the path. For any two vertices ''a'' and ''b'', write ''e''(''a'',''b'') for the sum e(a,b) = \sum_ \omega(P) over all paths from ''a'' to ''b''. This is well-defined if between any two points there are only finitely many paths; but even in the gene ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robinson–Schensted–Knuth Correspondence
In mathematics, the Robinson–Schensted–Knuth correspondence, also referred to as the RSK correspondence or RSK algorithm, is a combinatorial bijection between matrices with non-negative integer entries and pairs of semistandard Young tableaux of equal shape, whose size equals the sum of the entries of . More precisely the weight of is given by the column sums of , and the weight of by its row sums. It is a generalization of the Robinson–Schensted correspondence, in the sense that taking to be a permutation matrix, the pair will be the pair of standard tableaux associated to the permutation under the Robinson–Schensted correspondence. The Robinson–Schensted–Knuth correspondence extends many of the remarkable properties of the Robinson–Schensted correspondence, notably its symmetry: transposition of the matrix results in interchange of the tableaux . The Robinson–Schensted–Knuth correspondence Introduction The Robinson–Schensted correspondence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Group
In mathematics, a Lie group (pronounced ) is a group that is also a differentiable manifold. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additional properties it must have to be thought of as a "transformation" in the abstract sense, for instance multiplication and the taking of inverses (division), or equivalently, the concept of addition and the taking of inverses (subtraction). Combining these two ideas, one obtains a continuous group where multiplying points and their inverses are continuous. If the multiplication and taking of inverses are smooth (differentiable) as well, one obtains a Lie group. Lie groups provide a natural model for the concept of continuous symmetry, a celebrated example of which is the rotational symmetry in three dimensions (given by the special orthogonal group \text(3)). Lie groups are widely used in many parts of modern mathematics and physics. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unitary Group
In mathematics, the unitary group of degree ''n'', denoted U(''n''), is the group of unitary matrices, with the group operation of matrix multiplication. The unitary group is a subgroup of the general linear group . Hyperorthogonal group is an archaic name for the unitary group, especially over finite fields. For the group of unitary matrices with determinant 1, see Special unitary group. In the simple case , the group U(1) corresponds to the circle group, consisting of all complex numbers with absolute value 1, under multiplication. All the unitary groups contain copies of this group. The unitary group U(''n'') is a real Lie group of dimension ''n''2. The Lie algebra of U(''n'') consists of skew-Hermitian matrices, with the Lie bracket given by the commutator. The general unitary group (also called the group of unitary similitudes) consists of all matrices ''A'' such that ''A''∗''A'' is a nonzero multiple of the identity matrix, and is just the product of the uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Representation Theory Of The Symmetric Group
In mathematics, the representation theory of the symmetric group is a particular case of the representation theory of finite groups, for which a concrete and detailed theory can be obtained. This has a large area of potential applications, from symmetric function theory to quantum chemistry studies of atoms, molecules and solids. The symmetric group S''n'' has order ''n''!. Its conjugacy classes are labeled by partitions of ''n''. Therefore according to the representation theory of a finite group, the number of inequivalent irreducible representations, over the complex numbers, is equal to the number of partitions of ''n''. Unlike the general situation for finite groups, there is in fact a natural way to parametrize irreducible representations by the same set that parametrizes conjugacy classes, namely by partitions of ''n'' or equivalently Young diagrams of size ''n''. Each such irreducible representation can in fact be realized over the integers (every permutation acting by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gröbner Basis
In mathematics, and more specifically in computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating set of an ideal in a polynomial ring over a field . A Gröbner basis allows many important properties of the ideal and the associated algebraic variety to be deduced easily, such as the dimension and the number of zeros when it is finite. Gröbner basis computation is one of the main practical tools for solving systems of polynomial equations and computing the images of algebraic varieties under projections or rational maps. Gröbner basis computation can be seen as a multivariate, non-linear generalization of both Euclid's algorithm for computing polynomial greatest common divisors, and Gaussian elimination for linear systems. Gröbner bases were introduced in 1965, together with an algorithm to compute them ( Buchberger's algorithm), by Bruno Buchberger in his Ph.D. thesis. He named them ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hook Length Formula
In combinatorial mathematics, the hook length formula is a formula for the number of standard Young tableaux whose shape is a given Young diagram. It has applications in diverse areas such as representation theory, probability, and algorithm analysis; for example, the problem of longest increasing subsequences. A related formula gives the number of semi-standard Young tableaux, which is a specialization of a Schur polynomial. Definitions and statement Let \lambda=(\lambda_1\geq \cdots\geq \lambda_k) be a partition of n=\lambda_1+\cdots+\lambda_k. It is customary to interpret \lambda graphically as a Young diagram, namely a left-justified array of square cells with k rows of lengths \lambda_1,\ldots,\lambda_k. A (standard) Young tableau of shape \lambda is a filling of the n cells of the Young diagram with all the integers \, with no repetition, such that each row and each column form increasing sequences. For the cell in position (i,j), in the ith row and jth column, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pieri's Formula
In mathematics, Pieri's formula, named after Mario Pieri, describes the product of a Schubert cycle by a special Schubert cycle in the Schubert calculus, or the product of a Schur polynomial by a complete symmetric function. In terms of Schur functions ''s''λ indexed by partitions λ, it states that :\displaystyle s_\mu h_r=\sum_\lambda s_\lambda where ''h''''r'' is a complete homogeneous symmetric polynomial and the sum is over all partitions λ obtained from μ by adding ''r'' elements, no two in the same column. By applying the ω involution on the ring of symmetric functions, one obtains the dual Pieri rule for multiplying an elementary symmetric polynomial with a Schur polynomial: :\displaystyle s_\mu e_r=\sum_\lambda s_\lambda The sum is now taken over all partitions λ obtained from μ by adding ''r'' elements, no two in the same ''row''. Pieri's formula implies Giambelli's formula. The Littlewood–Richardson rule is a generalization ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew Tableau
In mathematics, a Young tableau (; plural: tableaux) is a combinatorial object useful in representation theory and Schubert calculus. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at Cambridge University, in 1900. They were then applied to the study of the symmetric group by Georg Frobenius in 1903. Their theory was further developed by many mathematicians, including Percy MacMahon, W. V. D. Hodge, G. de B. Robinson, Gian-Carlo Rota, Alain Lascoux, Marcel-Paul Schützenberger and Richard P. Stanley. Definitions ''Note: this article uses the English convention for displaying Young diagrams and tableaux''. Diagrams A Young diagram (also called a Ferrers diagram, particularly when represented using dots) is a finite collection of boxes, or cells, arranged in left-justified rows, with the row lengths in non-increasing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Murnaghan–Nakayama Rule
In group theory, a branch of mathematics, the Murnaghan–Nakayama rule, named after Francis Murnaghan and Tadashi Nakayama, is a combinatorial method to compute irreducible character values of a symmetric group.Richard Stanley, ''Enumerative Combinatorics, Vol. 2'' There are several generalizations of this rule beyond the representation theory of symmetric groups, but they are not covered here. The irreducible characters of a group are of interest to mathematicians because they concisely summarize important information about the group, such as the dimensions of the vector spaces in which the elements of the group can be represented by linear transformations that “mix” all the dimensions. For many groups, calculating irreducible character values is very difficult; the existence of simple formulas is the exception rather than the rule. The Murnaghan–Nakayama rule is a combinatorial rule for computing symmetric group character values χ using a particular kind of Young tab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hall–Littlewood Polynomials
In mathematics, the Hall–Littlewood polynomials are symmetric functions depending on a parameter ''t'' and a partition λ. They are Schur functions when ''t'' is 0 and monomial symmetric functions when ''t'' is 1 and are special cases of Macdonald polynomials. They were first defined indirectly by Philip Hall using the Hall algebra, and later defined directly by Dudley E. Littlewood (1961). Definition The Hall–Littlewood polynomial ''P'' is defined by :P_\lambda(x_1,\ldots,x_n;t) = \left( \prod_ \prod_^ \frac \right) , where λ is a partition of at most ''n'' with elements λ''i'', and ''m''(''i'') elements equal to ''i'', and ''S''''n'' is the symmetric group of order ''n''!. As an example, : P_(x_1,x_2;t) = x_1^4 x_2^2 + x_1^2 x_2^4 + (1-t) x_1^3 x_2^3 Specializations We have that P_\lambda(x;1) = m_\lambda(x), P_\lambda(x;0) = s_\lambda(x) and P_\lambda(x;-1) = P_\lambda(x) where the latter is the Schur ''P'' polynomials. Properties Expand ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |