|
SU(1,1)
In mathematics, the special unitary group of degree , denoted , is the Lie group of unitary matrices with determinant 1. The matrices of the more general unitary group may have complex determinants with absolute value 1, rather than real 1 in the special case. The group operation is matrix multiplication. The special unitary group is a normal subgroup of the unitary group , consisting of all unitary matrices. As a compact classical group, is the group that preserves the standard inner product on \mathbb^n. It is itself a subgroup of the general linear group, \operatorname(n) \subset \operatorname(n) \subset \operatorname(n, \mathbb ). The groups find wide application in the Standard Model of particle physics, especially in the electroweak interaction and in quantum chromodynamics. The simplest case, , is the trivial group, having only a single element. The group is isomorphic to the group of quaternions of norm 1, and is thus diffeomorphic to the 3-sphere. Since uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Quaternion
In mathematics, a versor is a quaternion of norm one, also known as a unit quaternion. Each versor has the form :u = \exp(a\mathbf) = \cos a + \mathbf \sin a, \quad \mathbf^2 = -1, \quad a \in ,\pi where the r2 = −1 condition means that r is an imaginary unit. There is a Quaternion#Square_roots_of_%E2%88%921, sphere of imaginary units in the quaternions. Note that the expression for a versor is just Euler's formula for the imaginary unit r. In case (a right angle), then u = \mathbf, and it is called a ''right versor''. The mapping q \to u^ q u corresponds to three-dimensional space, 3-dimensional rotation, and has the angle 2''a'' about the axis r in axis–angle representation. The collection of versors, with quaternion multiplication, forms a group (mathematics), group, and appears as a 3-sphere in the 4-dimensional quaternion algebra. Presentation on 3- and 2-spheres Hamilton denoted the versor of a quaternion ''q'' by the symbol U ''q''. He was then able to display t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Chromodynamics
In theoretical physics, quantum chromodynamics (QCD) is the study of the strong interaction between quarks mediated by gluons. Quarks are fundamental particles that make up composite hadrons such as the proton, neutron and pion. QCD is a type of quantum field theory called a non-abelian gauge theory, with symmetry group special unitary group, SU(3). The QCD analog of electric charge is a property called ''color''. Gluons are the force carriers of the theory, just as photons are for the electromagnetic force in quantum electrodynamics. The theory is an important part of the Standard Model of particle physics. A large body of Quantum chromodynamics#Experimental tests, experimental evidence for QCD has been gathered over the years. QCD exhibits three salient properties: * Color confinement. Due to the force between two color charges remaining constant as they are separated, the energy grows until a quark–antiquark pair is mass–energy equivalence, spontaneously produced, turning ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Group
In mathematics the spin group, denoted Spin(''n''), page 15 is a Lie group whose underlying manifold is the double cover of the special orthogonal group , such that there exists a short exact sequence of Lie groups (when ) :1 \to \mathbb_2 \to \operatorname(n) \to \operatorname(n) \to 1. The group multiplication law on the double cover is given by lifting the multiplication on \operatorname(n). As a Lie group, Spin(''n'') therefore shares its dimension, , and its Lie algebra with the special orthogonal group. For , Spin(''n'') is simply connected and so coincides with the universal cover of SO(''n''). The non-trivial element of the kernel is denoted −1, which should not be confused with the orthogonal transform of reflection through the origin, generally denoted −. Spin(''n'') can be constructed as a subgroup of the invertible elements in the Clifford algebra Cl(''n''). A distinct article discusses the spin representations. Use for physics models The spin group is use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
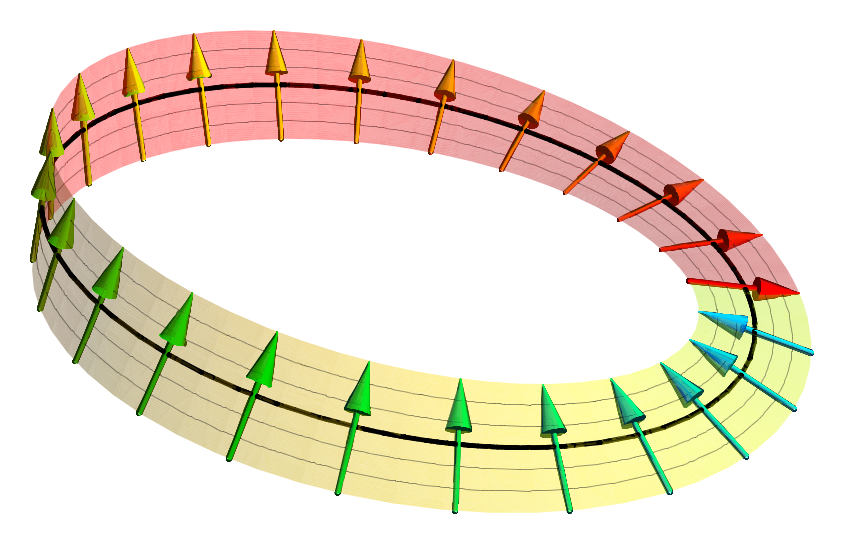
Spinor
In geometry and physics, spinors (pronounced "spinner" IPA ) are elements of a complex numbers, complex vector space that can be associated with Euclidean space. A spinor transforms linearly when the Euclidean space is subjected to a slight (infinitesimal transformation, infinitesimal) rotation, but unlike Euclidean vector, geometric vectors and tensors, a spinor transforms to its negative when the space rotates through 360° (see picture). It takes a rotation of 720° for a spinor to go back to its original state. This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of Section (fiber bundle), sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms). It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which cas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel (algebra)
In algebra, the kernel of a homomorphism is the relation describing how elements in the domain of the homomorphism become related in the image. A homomorphism is a function that preserves the underlying algebraic structure in the domain to its image. When the algebraic structures involved have an underlying group structure, the kernel is taken to be the preimage of the group's identity element in the image, that is, it consists of the elements of the domain mapping to the image's identity. For example, the map that sends every integer to its parity (that is, 0 if the number is even, 1 if the number is odd) would be a homomorphism to the integers modulo 2, and its respective kernel would be the even integers which all have 0 as its parity. The kernel of a homomorphism of group-like structures will only contain the identity if and only if the homomorphism is injective, that is if the inverse image of every element consists of a single element. This means that the kernel can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotation Group SO(3)
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space \R^3 under the operation of composition. By definition, a rotation about the origin is a transformation that preserves the origin, Euclidean distance (so it is an isometry), and orientation (i.e., ''handedness'' of space). Composing two rotations results in another rotation, every rotation has a unique inverse rotation, and the identity map satisfies the definition of a rotation. Owing to the above properties (along composite rotations' associative property), the set of all rotations is a group under composition. Every non-trivial rotation is determined by its axis of rotation (a line through the origin) and its angle of rotation. Rotations are not commutative (for example, rotating ''R'' 90° in the x-y plane followed by ''S'' 90° in the y-z plane is not the same as ''S'' followed by ''R''), making the 3D rotation grou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homomorphism
In algebra, a homomorphism is a morphism, structure-preserving map (mathematics), map between two algebraic structures of the same type (such as two group (mathematics), groups, two ring (mathematics), rings, or two vector spaces). The word ''homomorphism'' comes from the Ancient Greek language: () meaning "same" and () meaning "form" or "shape". However, the word was apparently introduced to mathematics due to a (mis)translation of German meaning "similar" to meaning "same". The term "homomorphism" appeared as early as 1892, when it was attributed to the German mathematician Felix Klein (1849–1925). Homomorphisms of vector spaces are also called linear maps, and their study is the subject of linear algebra. The concept of homomorphism has been generalized, under the name of morphism, to many other structures that either do not have an underlying set, or are not algebraic. This generalization is the starting point of category theory. A homomorphism may also be an isomorphis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surjective
In mathematics, a surjective function (also known as surjection, or onto function ) is a function such that, for every element of the function's codomain, there exists one element in the function's domain such that . In other words, for a function , the codomain is the image of the function's domain . It is not required that be unique; the function may map one or more elements of to the same element of . The term ''surjective'' and the related terms '' injective'' and ''bijective'' were introduced by Nicolas Bourbaki, a group of mainly French 20th-century mathematicians who, under this pseudonym, wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. The French word '' sur'' means ''over'' or ''above'', and relates to the fact that the image of the domain of a surjective function completely covers the function's codomain. Any function induces a surjection by restricting its codomain to the image of its domain. Every surjec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3-sphere
In mathematics, a hypersphere or 3-sphere is a 4-dimensional analogue of a sphere, and is the 3-dimensional n-sphere, ''n''-sphere. In 4-dimensional Euclidean space, it is the set of points equidistant from a fixed central point. The interior of a 3-sphere is a 4-ball. It is called a 3-sphere because topologically, the surface itself is 3-dimensional, even though it is curved into the 4th dimension. For example, when traveling on a 3-sphere, you can go north and south, east and west, or along a 3rd set of cardinal directions. This means that a 3-sphere is an example of a 3-manifold. Definition In coordinates, a 3-sphere with center and radius is the set of all points in real, Four-dimensional space, 4-dimensional space () such that :\sum_^3(x_i - C_i)^2 = ( x_0 - C_0 )^2 + ( x_1 - C_1 )^2 + ( x_2 - C_2 )^2+ ( x_3 - C_3 )^2 = r^2. The 3-sphere centered at the origin with radius 1 is called the unit 3-sphere and is usually denoted : :S^3 = \left\. It is often convenient to r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffeomorphic
In mathematics, a diffeomorphism is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable. Definition Given two differentiable manifolds M and N, a continuously differentiable map f \colon M \rightarrow N is a diffeomorphism if it is a bijection and its inverse f^ \colon N \rightarrow M is differentiable as well. If these functions are r times continuously differentiable, f is called a C^r-diffeomorphism. Two manifolds M and N are diffeomorphic (usually denoted M \simeq N) if there is a diffeomorphism f from M to N. Two C^r-differentiable manifolds are C^r-diffeomorphic if there is an r times continuously differentiable bijective map between them whose inverse is also r times continuously differentiable. Diffeomorphisms of subsets of manifolds Given a subset X of a manifold M and a subset Y of a manifold N, a function f:X ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quaternions is often denoted by (for ''Hamilton''), or in blackboard bold by \mathbb H. Quaternions are not a field, because multiplication of quaternions is not, in general, commutative. Quaternions provide a definition of the quotient of two vectors in a three-dimensional space. Quaternions are generally represented in the form a + b\,\mathbf i + c\,\mathbf j +d\,\mathbf k, where the coefficients , , , are real numbers, and , are the ''basis vectors'' or ''basis elements''. Quaternions are used in pure mathematics, but also have practical uses in applied mathematics, particularly for calculations involving three-dimensional rotations, such as in three-dimensional computer graphics, computer vision, robotics, magnetic resonance i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |