|
Richard Karp
Richard Manning Karp (born January 3, 1935) is an American computer scientist and computational theorist at the University of California, Berkeley. He is most notable for his research in the theory of algorithms, for which he received a Turing Award in 1985, The Benjamin Franklin Medal in Computer and Cognitive Science in 2004, and the Kyoto Prize in 2008. Karp was elected a member of the National Academy of Engineering (1992) for major contributions to the theory and application of NP-completeness, constructing efficient combinatorial algorithms, and applying probabilistic methods in computer science. Biography Born to parents Abraham and Rose Karp in Boston, Massachusetts, Karp has three younger siblings: Robert, David, and Carolyn. His family was Jewish,The Power and Limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Karp
{{disambiguation, geo, callsign ...
Karp may refer to: Places * Karp, Podlaskie Voivodeship, in north-east Poland * Karp, Lublin Voivodeship, in east Poland People * Karp (surname) * Karp Khachvankyan (1923–1998), Armenian actor and director Other uses * KARP-FM, a radio station in Dassel, Minnesota, United States * Karp (band), an American 1990s rock band * Karp class submarine, ordered in 1904 by the Russian Empire, also the namesake submarine in the class * Korean Association of Retired Persons, a non-governmental organization affiliated with the United Nations See also * Magikarp (Pokémon) * Carp (other) A carp is a type of fish. ''To carp'' is to Complaint (other), complain. Carp may also refer to: in watercraft: *USS F-1 (SS-20), USS ''Carp'' (SS-20), American submarine (1911–1917) *USS Carp (SS-338), USS ''Carp'' (SS-338), America ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ron Shamir
Ron Shamir (Hebrew: רון שמיר; born 29 November 1953) is an Israeli professor of computer science known for his work in graph theory and in computational biology. He holds the Raymond and Beverly Sackler Chair in Bioinformatics, and is the founder and head of the Edmond J. Safra Center for Bioinformatics at Tel Aviv University. Biography Ron Shamir was born in Jerusalem, Israel in 1953, the eldest son of Varda and Raphael Shamir. His father's Sepharadic family has lived in the old city of Jerusalem for over 400 years. His mother's parents were pioneers who came from Russia to Israel in the Third Aliyah in the early 1920s. He has two younger sisters, Daphna and Gadit. Shamir studied in Gymnasia Rehavia, Jerusalem, for 12 years. In high school, he was active in the scouts and in athletics; among other accomplishments, he won the Jerusalem high school championship in shot put. Shamir started his B.Sc. studies in mathematics and physics at Tel-Aviv University (1973–1975) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fulkerson Prize
The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Optimization Society (MOS) and the American Mathematical Society (AMS). Up to three awards of $1,500 each are presented at each (triennial) International Symposium of the MOS. Originally, the prizes were paid out of a memorial fund administered by the AMS that was established by friends of the late Delbert Ray Fulkerson to encourage mathematical excellence in the fields of research exemplified by his work. The prizes are now funded by an endowment administered by MPS. Winners SourceMathematical Optimization Society* 1979: ** Richard M. Karp for classifying many important NP-complete problems. ** Kenneth Appel and Wolfgang Haken for the four color theorem. ** Paul Seymour for generalizing the max-flow min-cut theorem to matroids. * 1982: ** D.B. Judin, Arkadi Nemirovski, Leonid Khachiyan, Martin Grötschel, László Lovász and Alexander Schrijver for the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Addition System
A vector addition system (VAS) is one of several mathematical modeling languages for the description of distributed systems. Vector addition systems were introduced by Richard M. Karp and Raymond E. Miller in 1969, and generalized to vector addition systems with states (VASS) by John E. Hopcroft and Jean-Jacques Pansiot in 1979. Both VAS and VASS are equivalent in many ways to Petri nets introduced earlier by Carl Adam Petri. Reachability in vector addition systems is Ackermann-complete (and hence nonelementary). Informal definition A ''vector addition system'' consists of a finite set of integer vectors. An initial vector is seen as the initial values of multiple counters, and the vectors of the VAS are seen as updates. These counters may never drop below zero. More precisely, given an initial vector with non negative values, the vectors of the VAS can be added componentwise, given that every intermediate vector has non negative values. A ''vector addition system with st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Karp's 21 NP-complete Problems
In computational complexity theory, Karp's 21 NP-complete problems are a set of computational problems which are NP-complete. In his 1972 paper, "Reducibility Among Combinatorial Problems", Richard Karp used Stephen Cook's 1971 theorem that the boolean satisfiability problem is NP-complete (also called the Cook-Levin theorem) to show that there is a polynomial time many-one reduction from the boolean satisfiability problem to each of 21 combinatorial and graph theoretical computational problems, thereby showing that they are all NP-complete. This was one of the first demonstrations that many natural computational problems occurring throughout computer science are computationally intractable, and it drove interest in the study of NP-completeness and the P versus NP problem. The problems Karp's 21 problems are shown below, many with their original names. The nesting indicates the direction of the reductions used. For example, Knapsack was shown to be NP-complete by reducing Exact ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Karp–Lipton Theorem
In complexity theory, the Karp–Lipton theorem states that if the Boolean satisfiability problem (SAT) can be solved by Boolean circuits with a polynomial number of logic gates, then :\Pi_2 = \Sigma_2 \, and therefore \mathrm = \Sigma_2. \, That is, if we assume that NP, the class of nondeterministic polynomial time problems, can be contained in the non-uniform polynomial time complexity class P/poly, then this assumption implies the collapse of the polynomial hierarchy at its second level. Such a collapse is believed unlikely, so the theorem is generally viewed by complexity theorists as evidence for the nonexistence of polynomial size circuits for SAT or for other NP-complete problems. A proof that such circuits do not exist would imply that P ≠ NP. As P/poly contains all problems solvable in randomized polynomial time (Adleman's theorem), the theorem is also evidence that the use of randomization does not lead to polynomial time algorithms for NP-complete problems. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Karmarkar–Karp Algorithm
In computer science, the largest differencing method is an algorithm for solving the partition problem and the multiway number partitioning. It is also called the Karmarkar–Karp algorithm after its inventors, Narendra Karmarkar and Richard M. Karp. It is often abbreviated as LDM. The algorithm The input to the algorithm is a set ''S'' of numbers, and a parameter ''k''. The required output is a partition of ''S'' into ''k'' subsets, such that the sums in the subsets are as nearly equal as possible. The main steps of the algorithm are: # Order the numbers from large to small. #Replace the largest and second-largest numbers by their difference. #If two or more numbers remain, return to step 1. # Using backtracking, compute the partition. Two-way partitioning For ''k''=2, the main step (2) works as follows. * Take the two largest numbers in ''S'', remove them from ''S'', and insert their difference (this represents a decision to put each of these numbers in a different subset) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
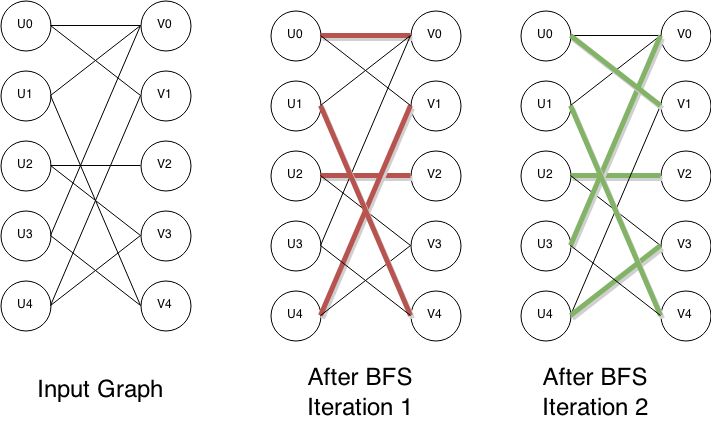
Hopcroft–Karp Algorithm
In computer science, the Hopcroft–Karp algorithm (sometimes more accurately called the Hopcroft–Karp–Karzanov algorithm) is an algorithm that takes a bipartite graph as input and produces a maximum cardinality matching as output – a set of as many edges as possible with the property that no two edges share an endpoint. It runs in O(, E, \sqrt) time in the worst case, where E is set of edges in the graph, V is set of vertices of the graph, and it is assumed that , E, =\Omega(, V, ). In the case of dense graphs the time bound becomes O(, V, ^), and for sparse random graphs it runs in time O(, E, \log , V, ) with high probability. The algorithm was discovered by and independently by . As in previous methods for matching such as the Hungarian algorithm and the work of , the Hopcroft–Karp algorithm repeatedly increases the size of a partial matching by finding ''augmenting paths''. These paths are sequences of edges of the graph, which alternate between edges in the matching ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Held–Karp Algorithm
The Held–Karp algorithm, also called Bellman–Held–Karp algorithm, is a dynamic programming algorithm proposed in 1962 independently by Bellman and by Held and Karp to solve the traveling salesman problem (TSP), in which the input is a distance matrix between a set of cities, and the goal is to find a minimum-length tour that visits each city exactly once before returning to the starting point. It finds the exact solution to this problem, and to several related problems including the Hamiltonian cycle problem, in exponential time. Algorithm description and motivation Number the cities 1, 2, \ldots, n, with 1 designated arbitrarily as a "starting" city (since the solution to TSP is a cycle, the choice of starting city doesn't matter). The Held–Karp algorithm begins by calculating, for each set of cities S \subseteq \ and every city e \neq 1 not contained in S, the shortest one-way path from 1 to e that passes through every city in S in some order (but not through any other c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edmonds–Karp Algorithm
In computer science, the Edmonds–Karp algorithm is an implementation of the Ford–Fulkerson method for computing the maximum flow in a flow network in O(, V, , E, ^2) time. The algorithm was first published by Yefim Dinitz (whose name is also transliterated "E. A. Dinic", notably as author of his early papers) in 1970 and independently published by Jack Edmonds and Richard Karp in 1972. Dinic's algorithm includes additional techniques that reduce the running time to O(, V, ^2, E, ). Algorithm The algorithm is identical to the Ford–Fulkerson algorithm, except that the search order when finding the augmenting path is defined. The path found must be a shortest path that has available capacity. This can be found by a breadth-first search, where we apply a weight of 1 to each edge. The running time of O(, V, , E, ^2) is found by showing that each augmenting path can be found in O(, E, ) time, that every time at least one of the E edges becomes saturated (an edge which has the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aanderaa–Karp–Rosenberg Conjecture
In theoretical computer science, the Aanderaa–Karp–Rosenberg conjecture (also known as the Aanderaa–Rosenberg conjecture or the evasiveness conjecture) is a group of related conjectures about the number of questions of the form "Is there an edge between vertex u and vertex v?" that have to be answered to determine whether or not an undirected graph has a particular property such as planarity or bipartiteness. They are named after Stål Aanderaa, Richard M. Karp, and Arnold L. Rosenberg. According to the conjecture, for a wide class of properties, no algorithm can guarantee that it will be able to skip any questions: any algorithm for determining whether the graph has the property, no matter how clever, might need to examine every pair of vertices before it can give its answer. A property satisfying this conjecture is called evasive. More precisely, the Aanderaa–Rosenberg conjecture states that any deterministic algorithm must test at least a constant fraction of all pos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
