|
Ratio Distribution
A ratio distribution (also known as a quotient distribution) is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two (usually statistically independent, independent) random variables ''X'' and ''Y'', the distribution of the random variable ''Z'' that is formed as the ratio ''Z'' = ''X''/''Y'' is a ''ratio distribution''. An example is the Cauchy distribution (also called the ''normal ratio distribution''), which comes about as the ratio of two normal distribution, normally distributed variables with zero mean. Two other distributions often used in test-statistics are also ratio distributions: the Student's t-distribution, ''t''-distribution arises from a Gaussian distribution, Gaussian random variable divided by an independent chi distribution, chi-distributed random variable, while the F-distribution, ''F''-distribution originates from the ratio of two independent chi-squared distribution, chi- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Probability Distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical description of a Randomness, random phenomenon in terms of its sample space and the Probability, probabilities of Event (probability theory), events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that fair coin, the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Management Science (journal)
''Management Science'' is a peer-reviewed academic journal that covers research on all aspects of management related to strategy, entrepreneurship, innovation, information technology, and organizations as well as all functional areas of business, such as accounting, finance, marketing, and operations. It is published by the Institute for Operations Research and the Management Sciences and was established in 1954 by the institute's precursor, the Institute of Management Sciences. C. West Churchman was the founding editor-in-chief. According to the ''Journal Citation Reports'', the journal has a 2022 impact factor of 5.4. Editors-in-chief The following persons are, or have been, editors-in-chief: *2018–2023: David Simchi-Levi *2014–2018: Teck-Hua Ho *2009–2014: Gérard Cachon *2003–2008: Wallace Hopp *1997–2002: Hau L. Lee *1993–1997: Gabriel R. Bitran *1983–1990: Donald G. Morrison *1968–1983: Martin K. Starr *1960–1967: Robert M. Thrall *1954–1960: C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
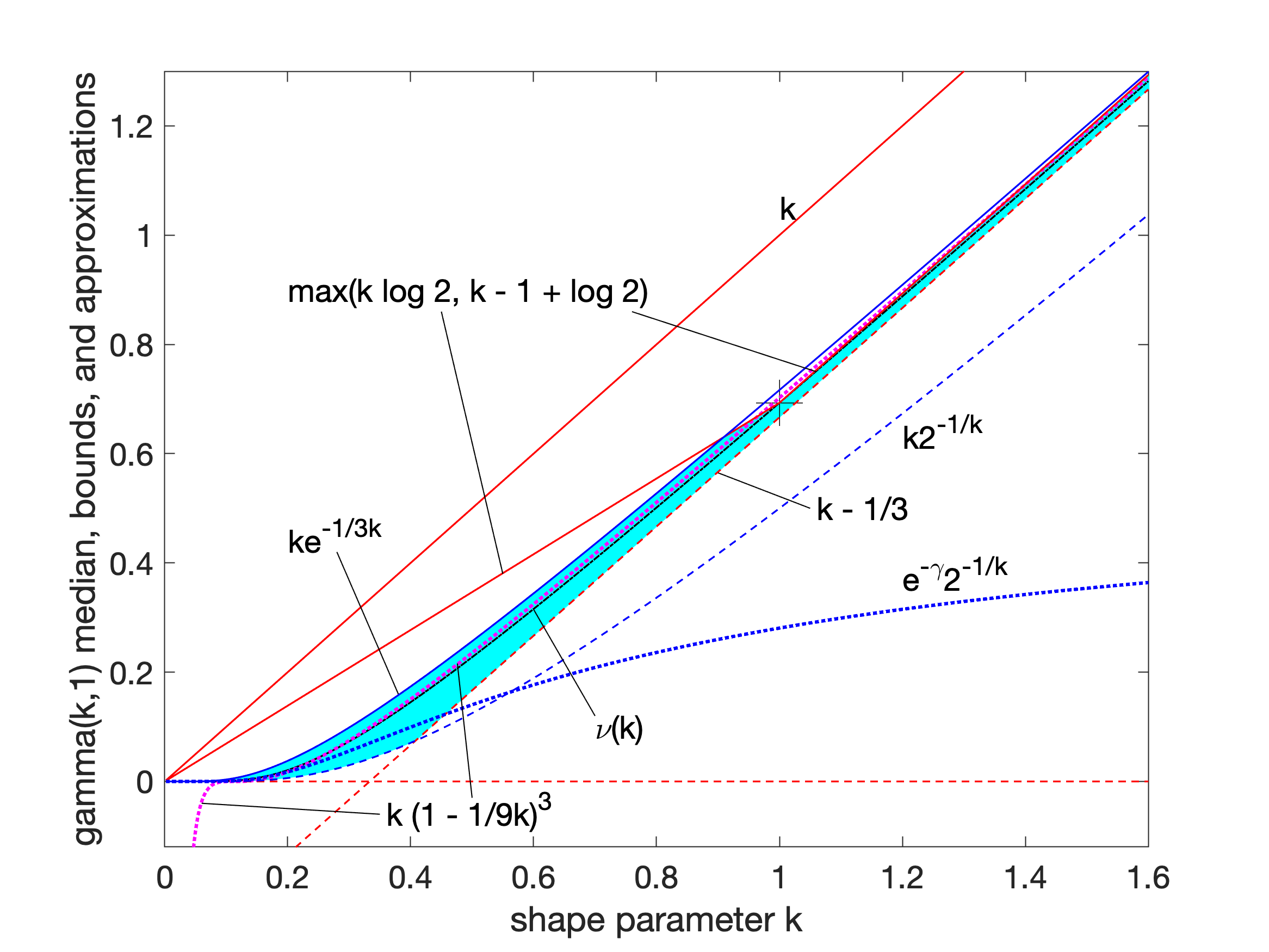
Gamma Distribution
In probability theory and statistics, the gamma distribution is a versatile two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: # With a shape parameter and a scale parameter # With a shape parameter \alpha and a rate parameter In each of these forms, both parameters are positive real numbers. The distribution has important applications in various fields, including econometrics, Bayesian statistics, and life testing. In econometrics, the (''α'', ''θ'') parameterization is common for modeling waiting times, such as the time until death, where it often takes the form of an Erlang distribution for integer ''α'' values. Bayesian statisticians prefer the (''α'',''λ'') parameterization, utilizing the gamma distribution as a conjugate prior for several inverse scale parameters, facilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mellin Transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform. This integral transform is closely connected to the theory of Dirichlet series, and is often used in number theory, mathematical statistics, and the theory of asymptotic expansions; it is closely related to the Laplace transform and the Fourier transform, and the theory of the gamma function and allied special functions. The Mellin transform of a complex-valued function defined on \mathbf R^_+= (0,\infty) is the function \mathcal M f of complex variable s given (where it exists, see Fundamental strip below) by \mathcal\left\(s) = \varphi(s)=\int_0^\infty x^ f(x) \, dx = \int_f(x) x^s \frac. Notice that dx/x is a Haar measure on the multiplicative group \mathbf R^_+ and x\mapsto x^s is a (in general non-unitary) multiplicative character. The inverse transform is \mathcal^\left\(x) = f(x)=\frac \int_^ x^ \varphi(s)\, ds. The notation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Melvin D
Melvin is a masculine given name and surname, likely a variant of Melville and a descendant of the French surname de Maleuin and the later Melwin. It may alternatively be spelled as Melvyn or, in Welsh, Melfyn and the name Melivinia or Melva may be used a feminine form. Of Norman French origin, originally Malleville, which translates to "bad town," it likely made its way into usage in Scotland as a result of the Norman conquest of England. It came into use as a given name as early as the 19th century, in English-speaking populations. As a name Given name Academics * Melvin Calvin (1911–1997), American chemist who discovered the Calvin cycle * Melvin Day (1923–2016), New Zealand artist and art historian *Melvin Hochster (born 1943), American mathematician *Melvin Konner (born 1946), Professor of Anthropology *Melvin Schwartz (1932–2006), American physicist who won the Nobel Prize in Physics in 1988 * Melvin Alvah Traylor, Jr. (1915–2008), American ornithologist Busin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Difference Distribution
Difference commonly refers to: * Difference (philosophy), the set of properties by which items are distinguished * Difference (mathematics), the result of a subtraction Difference, The Difference, Differences or Differently may also refer to: Music * ''Difference'' (album), by Dreamtale, 2005 * ''The Difference'' (album), Pendleton, 2008 * "The Difference" (The Wallflowers song), 1997 * "Differences" (song), by Ginuwine, 2001 * ''Differently'' (album), by Cassie Davis, 2009 ** "Differently" (song), by Cassie Davis, 2009 * "Difference", a song by Benjamin Clementine from the 2022 album ''And I Have Been'' * "The Difference", a song by Matchbox Twenty from the 2002 album '' More Than You Think You Are'' * "The Difference", a song by Westlife from the 2009 album ''Where We Are'' * "The Difference", a song by Nick Jonas from the 2016 album '' Last Year Was Complicated'' * "The Difference", a song by Meek Mill featuring Quavo, from the 2016 mixtape '' DC4'' * "The Difference", a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sum Distribution
Sum most commonly means the total of two or more numbers added together; see addition. Sum can also refer to: Mathematics * Sum (category theory), the generic concept of summation in mathematics * Sum, the result of summation, the addition of a sequence of numbers * 3SUM, a term from computational complexity theory * Band sum, a way of connecting mathematical knots * Connected sum, a way of gluing manifolds * Digit sum, in number theory * Direct sum, a combination of algebraic objects ** Direct sum of groups ** Direct sum of modules ** Direct sum of permutations ** Direct sum of topological groups * Einstein summation, a way of contracting tensor indices * Empty sum, a sum with no terms * Indefinite sum, the inverse of a finite difference * Kronecker sum, an operation considered a kind of addition for matrices * Matrix addition, in linear algebra * Minkowski addition, a sum of two subsets of a vector space * Power sum symmetric polynomial, in commutative algebra * Prefix ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
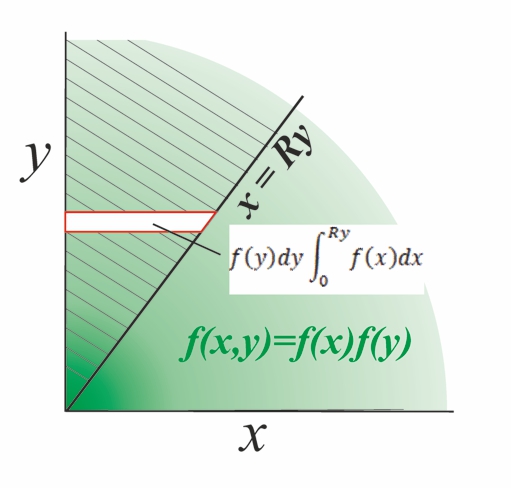
Product Distribution
A product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions. Given two statistically independent random variables ''X'' and ''Y'', the distribution of the random variable ''Z'' that is formed as the product Z = XY is a ''product distribution''. The product distribution is the PDF of the product of sample values. This is not the same as the product of their PDFs yet the concepts are often ambiguously termed as in "product of Gaussians". Algebra of random variables The product is one type of algebra for random variables: Related to the product distribution are the ratio distribution, sum distribution (see List of convolutions of probability distributions) and difference distribution. More generally, one may talk of combinations of sums, differences, products and ratios. Many of these distributions are described in Melvin D. Springer's book from 1979 ''The Algebra of Random Variable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Proc Natl Acad Sci U S A
''Proceedings of the National Academy of Sciences of the United States of America'' (often abbreviated ''PNAS'' or ''PNAS USA'') is a peer-reviewed multidisciplinary scientific journal. It is the official journal of the National Academy of Sciences, published since 1915, and publishes original research, scientific reviews, commentaries, and letters. According to ''Journal Citation Reports'', the journal has a 2022 impact factor of 9.4. ''PNAS'' is the second most cited scientific journal, with more than 1.9 million cumulative citations from 2008 to 2018. In the past, ''PNAS'' has been described variously as "prestigious", "sedate", "renowned" and "high impact". ''PNAS'' is a delayed open-access journal, with an embargo period of six months that can be bypassed for an author fee ( hybrid open access). Since September 2017, open access articles are published under a Creative Commons license. Since January 2019, ''PNAS'' has been online-only, although print issues are available ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Median
The median of a set of numbers is the value separating the higher half from the lower half of a Sample (statistics), data sample, a statistical population, population, or a probability distribution. For a data set, it may be thought of as the “middle" value. The basic feature of the median in describing data compared to the Arithmetic mean, mean (often simply described as the "average") is that it is not Skewness, skewed by a small proportion of extremely large or small values, and therefore provides a better representation of the center. Median income, for example, may be a better way to describe the center of the income distribution because increases in the largest incomes alone have no effect on the median. For this reason, the median is of central importance in robust statistics. Median is a 2-quantile; it is the value that partitions a set into two equal parts. Finite set of numbers The median of a finite list of numbers is the "middle" number, when those numbers are liste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
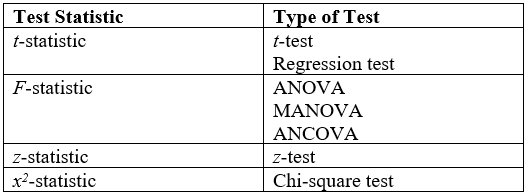
Statistical Test
A statistical hypothesis test is a method of statistical inference used to decide whether the data provide sufficient evidence to reject a particular hypothesis. A statistical hypothesis test typically involves a calculation of a test statistic. Then a decision is made, either by comparing the test statistic to a critical value or equivalently by evaluating a ''p''-value computed from the test statistic. Roughly 100 specialized statistical tests are in use and noteworthy. History While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Choice of null hypothesis Paul Meehl has argued that the epistemological importance of the choice of null hypothesis has gone largely unacknowledged. When the null hypothesis is predicted by theory, a more precise experiment will be a more severe tes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |