|
Product Distribution
A product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions. Given two statistically independent random variables ''X'' and ''Y'', the distribution of the random variable ''Z'' that is formed as the product Z = XY is a ''product distribution''. Algebra of random variables The product is one type of algebra for random variables: Related to the product distribution are the ratio distribution, sum distribution (see List of convolutions of probability distributions) and difference distribution. More generally, one may talk of combinations of sums, differences, products and ratios. Many of these distributions are described in Melvin D. Springer's book from 1979 ''The Algebra of Random Variables''. Derivation for independent random variables If X and Y are two independent, continuous random variables, described by probability density functions f_X and f_Y then the probability density ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that the coin is fair). Examples of random phenomena include the weather conditions at some future date, the height of a randomly selected person, the fraction of male students in a school, the results of a survey to be conducted, etc. Introduction A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The sample space, often denoted by \Omega, is the set of all possible outcomes of a ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
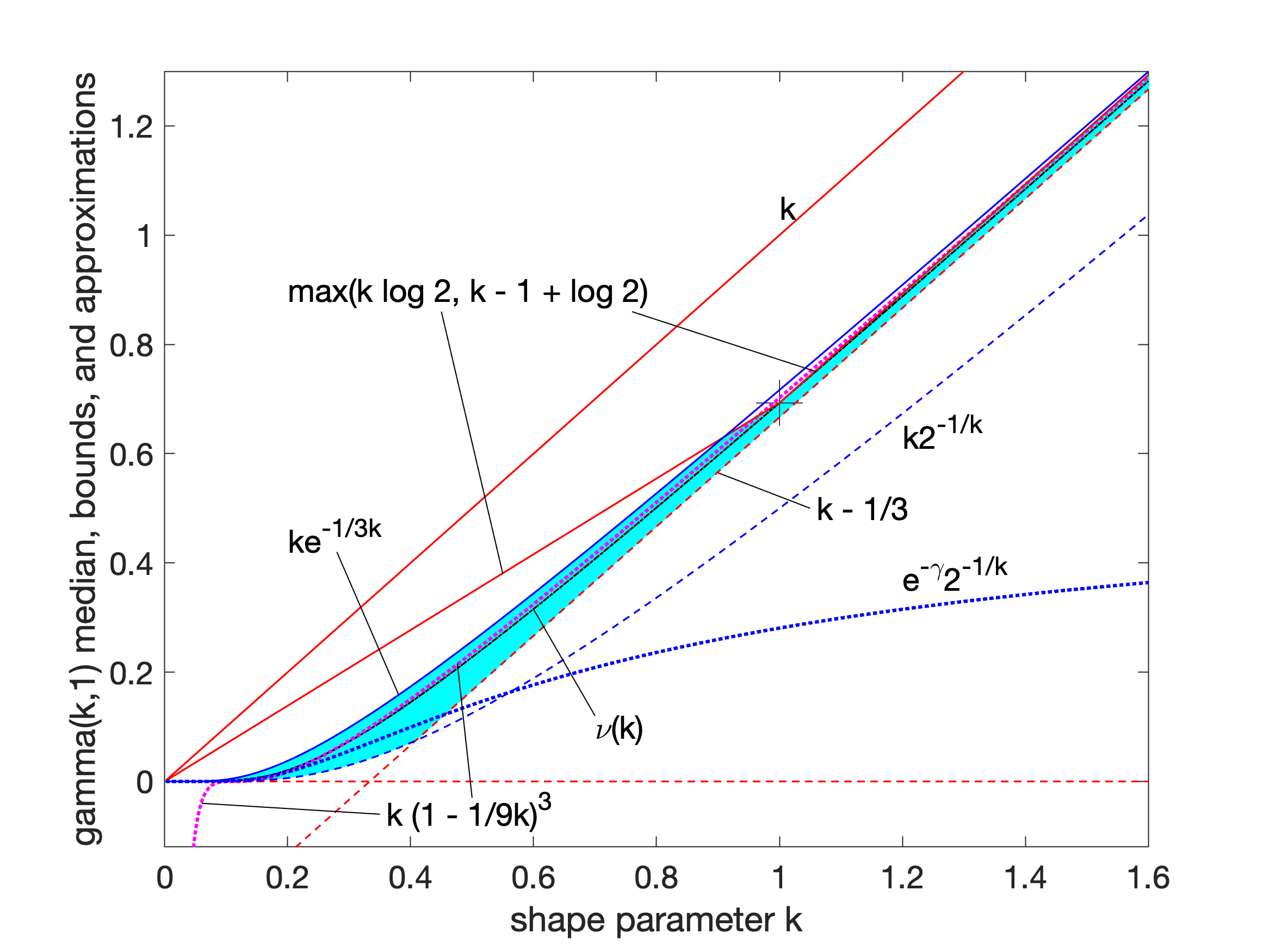
Gamma Distribution
In probability theory and statistics, the gamma distribution is a two- parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-square distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: #With a shape parameter k and a scale parameter \theta. #With a shape parameter \alpha = k and an inverse scale parameter \beta = 1/ \theta , called a rate parameter. In each of these forms, both parameters are positive real numbers. The gamma distribution is the maximum entropy probability distribution (both with respect to a uniform base measure and a 1/x base measure) for a random variable X for which E 'X''= ''kθ'' = ''α''/''β'' is fixed and greater than zero, and E n(''X'')= ''ψ''(''k'') + ln(''θ'') = ''ψ''(''α'') − ln(''β'') is fixed (''ψ'' is the digamma function). Definitions The parameterization with ''k'' and ''θ'' appears to be more common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wishart Distribution
In statistics, the Wishart distribution is a generalization to multiple dimensions of the gamma distribution. It is named in honor of John Wishart, who first formulated the distribution in 1928. It is a family of probability distributions defined over symmetric, nonnegative-definite random matrices (i.e. matrix-valued random variables). In random matrix theory, the space of Wishart matrices is called the ''Wishart ensemble''. These distributions are of great importance in the estimation of covariance matrices in multivariate statistics. In Bayesian statistics, the Wishart distribution is the conjugate prior of the inverse covariance-matrix of a multivariate-normal random-vector. Definition Suppose is a matrix, each column of which is independently drawn from a -variate normal distribution with zero mean: :G_ = (g_i^1,\dots,g_i^p)^T\sim \mathcal_p(0,V). Then the Wishart distribution is the probability distribution of the random matrix :S= G G^T = \sum_^n G_G_^T kn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Multivariate Analysis
The ''Journal of Multivariate Analysis'' is a monthly peer-reviewed scientific journal that covers applications and research in the field of multivariate statistical analysis. The journal's scope includes theoretical results as well as applications of new theoretical methods in the field. Some of the research areas covered include copula modeling, functional data analysis, graphical modeling, high-dimensional data analysis, image analysis, multivariate extreme-value theory, sparse modeling, and spatial statistics. According to the ''Journal Citation Reports'', the journal has a 2017 impact factor of 1.009. See also *List of statistics journals This is a list of scientific journals published in the field of statistics. Introductory and outreach *''The American Statistician'' *'' Significance'' General theory and methodology *''Annals of the Institute of Statistical Mathematics'' *''An ... References External links * {{DEFAULTSORT:Journal of Multivariate Analysis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double Factorial
In mathematics, the double factorial or semifactorial of a number , denoted by , is the product of all the integers from 1 up to that have the same parity (odd or even) as . That is, :n!! = \prod_^ (n-2k) = n (n-2) (n-4) \cdots. For even , the double factorial is :n!! = \prod_^\frac (2k) = n(n-2)(n-4)\cdots 4\cdot 2 \,, and for odd it is :n!! = \prod_^\frac (2k-1) = n(n-2)(n-4)\cdots 3\cdot 1 \,. For example, . The zero double factorial as an empty product. The sequence of double factorials for even = starts as : 1, 2, 8, 48, 384, 3840, 46080, 645120,... The sequence of double factorials for odd = starts as : 1, 3, 15, 105, 945, 10395, 135135,... The term odd factorial is sometimes used for the double factorial of an odd number. History and usage In a 1902 paper, the physicist Arthur Schuster wrote: states that the double factorial was originally introduced in order to simplify the expression of certain trigonometric integrals that arise in the derivation of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisher Transformation
In statistics, the Fisher transformation (or Fisher ''z''-transformation) of a Pearson correlation coefficient is its inverse hyperbolic tangent (artanh). When the sample correlation coefficient ''r'' is near 1 or -1, its distribution is highly skewed, which makes it difficult to estimate confidence intervals and apply tests of significance for the population correlation coefficient ρ. The Fisher transformation solves this problem by yielding a variable whose distribution is approximately normally distributed, with a variance that is stable over different values of ''r''. Definition Given a set of ''N'' bivariate sample pairs (''X''''i'', ''Y''''i''), ''i'' = 1, …, ''N'', the sample correlation coefficient ''r'' is given by :r = \frac = \frac. Here \operatorname(X,Y) stands for the covariance between the variables X and Y and \sigma stands for the standard deviation of the respective variable. Fisher's z-transformation of ''r'' is defined ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chi-squared Distribution
In probability theory and statistics, the chi-squared distribution (also chi-square or \chi^2-distribution) with k degrees of freedom is the distribution of a sum of the squares of k independent standard normal random variables. The chi-squared distribution is a special case of the gamma distribution and is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing and in construction of confidence intervals. This distribution is sometimes called the central chi-squared distribution, a special case of the more general noncentral chi-squared distribution. The chi-squared distribution is used in the common chi-squared tests for goodness of fit of an observed distribution to a theoretical one, the independence of two criteria of classification of qualitative data, and in confidence interval estimation for a population standard deviation of a normal distribution from a sample standard deviation. Many other statistical tes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modified Bessel Function
Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions of Bessel's differential equation x^2 \frac + x \frac + \left(x^2 - \alpha^2 \right)y = 0 for an arbitrary complex number \alpha, the ''order'' of the Bessel function. Although \alpha and -\alpha produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of \alpha. The most important cases are when \alpha is an integer or half-integer. Bessel functions for integer \alpha are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to Laplace's equation in cylindrical coordinates. Spherical Bessel functions with half-integer \alpha are obtained when the Helmholtz equation is solved in spherical coordinates. Applications of Bessel functions The Bessel function is a generalization ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characteristic Function (probability Theory)
In probability theory and statistics, the characteristic function of any real-valued random variable completely defines its probability distribution. If a random variable admits a probability density function, then the characteristic function is the Fourier transform of the probability density function. Thus it provides an alternative route to analytical results compared with working directly with probability density functions or cumulative distribution functions. There are particularly simple results for the characteristic functions of distributions defined by the weighted sums of random variables. In addition to univariate distributions, characteristic functions can be defined for vector- or matrix-valued random variables, and can also be extended to more generic cases. The characteristic function always exists when treated as a function of a real-valued argument, unlike the moment-generating function. There are relations between the behavior of the characteristic function of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Copula (probability Theory)
In probability theory and statistics, a copula is a multivariate cumulative distribution function for which the marginal probability distribution of each variable is uniform on the interval , 1 Copulas are used to describe/model the dependence (inter-correlation) between random variables. Their name, introduced by applied mathematician Abe Sklar in 1959, comes from the Latin for "link" or "tie", similar but unrelated to grammatical copulas in linguistics. Copulas have been used widely in quantitative finance to model and minimize tail risk and portfolio-optimization applications. Sklar's theorem states that any multivariate joint distribution can be written in terms of univariate marginal distribution functions and a copula which describes the dependence structure between the variables. Copulas are popular in high-dimensional statistical applications as they allow one to easily model and estimate the distribution of random vectors by estimating marginals and cop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |