|
Rényi Entropy
In information theory, the Rényi entropy is a quantity that generalizes various notions of Entropy (information theory), entropy, including Hartley entropy, Shannon entropy, collision entropy, and min-entropy. The Rényi entropy is named after Alfréd Rényi, who looked for the most general way to quantify information while preserving additivity for independent events. In the context of fractal dimension estimation, the Rényi entropy forms the basis of the concept of generalized dimensions. The Rényi entropy is important in ecology and statistics as diversity indices, index of diversity. The Rényi entropy is also important in quantum information, where it can be used as a measure of Quantum entanglement, entanglement. In the Heisenberg XY spin chain model, the Rényi entropy as a function of can be calculated explicitly because it is an automorphic function with respect to a particular subgroup of the modular group. In theoretical computer science, the min-entropy is used in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Information Theory
Information theory is the mathematical study of the quantification (science), quantification, Data storage, storage, and telecommunications, communication of information. The field was established and formalized by Claude Shannon in the 1940s, though early contributions were made in the 1920s through the works of Harry Nyquist and Ralph Hartley. It is at the intersection of electronic engineering, mathematics, statistics, computer science, Neuroscience, neurobiology, physics, and electrical engineering. A key measure in information theory is information entropy, entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a Fair coin, fair coin flip (which has two equally likely outcomes) provides less information (lower entropy, less uncertainty) than identifying the outcome from a roll of a dice, die (which has six equally likely outcomes). Some other important measu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Shannon (unit)
The shannon (symbol: Sh) is a unit of information named after Claude Shannon, the founder of information theory. IEC 80000-13 defines the shannon as the information content associated with an event when the probability of the event occurring is . It is understood as such within the realm of information theory, and is conceptually distinct from the bit, a term used in data processing and storage to denote a single instance of a binary signal. A sequence of ''n'' binary symbols (such as contained in computer memory or a binary data transmission) is properly described as consisting of ''n'' bits, but the information content of those ''n'' symbols may be more or less than ''n'' shannons depending on the ''a priori'' probability of the actual sequence of symbols. The shannon also serves as a unit of the information entropy of an event, which is defined as the expected value of the information content of the event (i.e., the probability-weighted average of the information content of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Jensen's Inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906, building on an earlier proof of the same inequality for doubly-differentiable functions by Otto Hölder in 1889. Given its generality, the inequality appears in many forms depending on the context, some of which are presented below. In its simplest form the inequality states that the convex transformation of a mean is less than or equal to the mean applied after convex transformation (or equivalently, the opposite inequality for concave transformations). Jensen's inequality generalizes the statement that the secant line of a convex function lies ''above'' the graph of the function, which is Jensen's inequality for two points: the secant line consists of weighted means of the convex function (for ''t'' ∈ ,1, :t f(x_1) + (1-t) f(x_2), while the g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
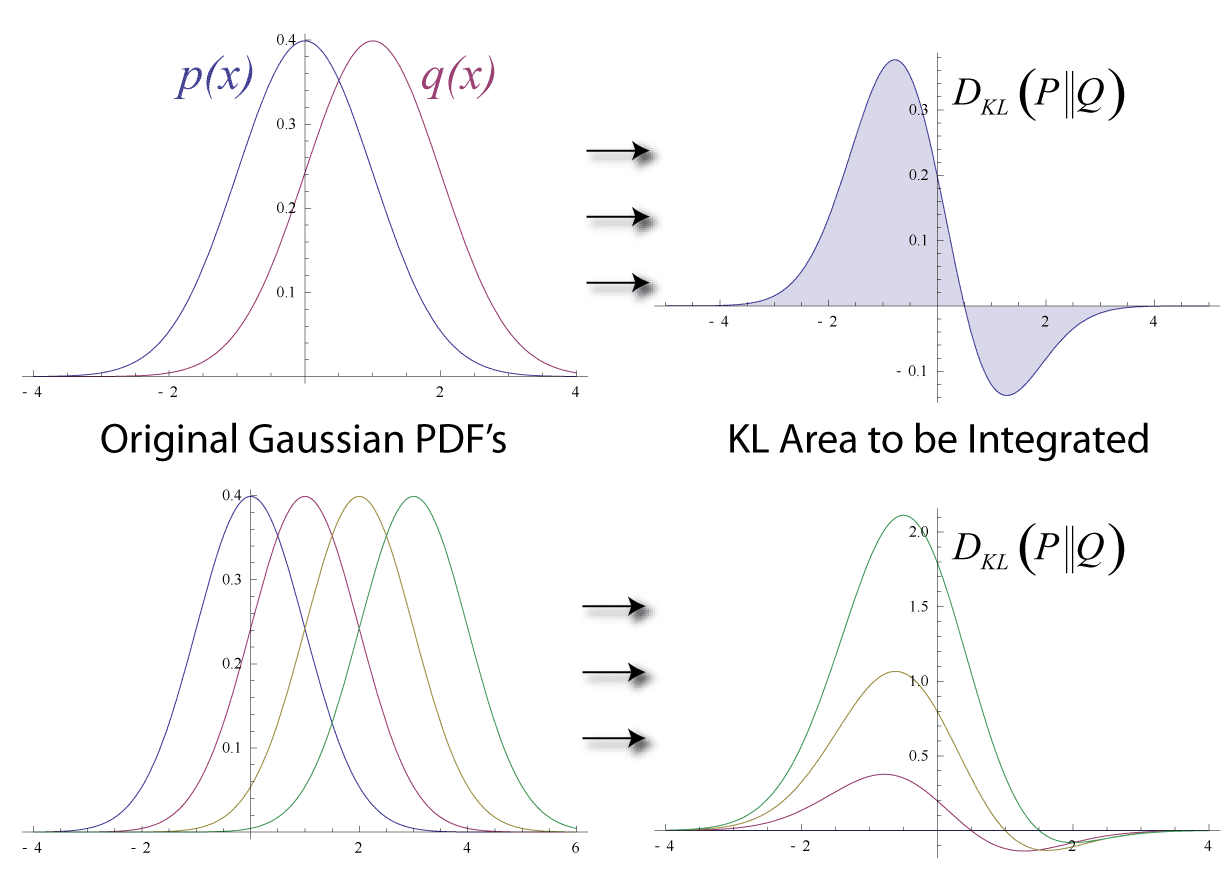
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler (KL) divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how much a model probability distribution is different from a true probability distribution . Mathematically, it is defined as D_\text(P \parallel Q) = \sum_ P(x) \, \log \frac\text A simple interpretation of the KL divergence of from is the expected excess surprise from using as a model instead of when the actual distribution is . While it is a measure of how different two distributions are and is thus a distance in some sense, it is not actually a metric, which is the most familiar and formal type of distance. In particular, it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for cer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Index Of Coincidence
In cryptography, coincidence counting is the technique (invented by William F. Friedman) of putting two texts side-by-side and counting the number of times that identical letters appear in the same position in both texts. This count, either as a ratio of the total or normalized by dividing by the expected count for a random source model, is known as the index of coincidence, or IC or IOC or IoC for short. Because letters in a natural language are not letter frequency, distributed evenly, the IC is higher for such texts than it would be for uniformly random text strings. What makes the IC especially useful is the fact that its value does not change if both texts are scrambled by the same single-alphabet substitution cipher, allowing a cryptanalyst to quickly detect that form of encryption. Calculation The index of coincidence provides a measure of how likely it is to draw two matching letters by randomly selecting two letters from a given text. The chance of drawing a given letter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Independent And Identically Distributed
Independent or Independents may refer to: Arts, entertainment, and media Artist groups * Independents (artist group), a group of modernist painters based in Pennsylvania, United States * Independentes (English: Independents), a Portuguese artist group Music Groups, labels, and genres * Independent music, a number of genres associated with independent labels * Independent record label, a record label not associated with a major label * Independent Albums, American albums chart Albums * ''Independent'' (Ai album), 2012 * ''Independent'' (Faze album), 2006 * ''Independent'' (Sacred Reich album), 1993 Songs * "Independent" (song), a 2007 song by Webbie * "Independent", a 2002 song by Ayumi Hamasaki from '' H'' News media organizations * Independent Media Center (also known as Indymedia or IMC), an open publishing network of journalist collectives that report on political and social issues, e.g., in ''The Indypendent'' newspaper of NYC * ITV (TV network) (Independent Television ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cardinality
The thumb is the first digit of the hand, next to the index finger. When a person is standing in the medical anatomical position (where the palm is facing to the front), the thumb is the outermost digit. The Medical Latin English noun for thumb is ''pollex'' (compare ''hallux'' for big toe), and the corresponding adjective for thumb is ''pollical''. Definition Thumb and fingers The English word ''finger'' has two senses, even in the context of appendages of a single typical human hand: 1) Any of the five terminal members of the hand. 2) Any of the four terminal members of the hand, other than the thumb. Linguistically, it appears that the original sense was the first of these two: (also rendered as ) was, in the inferred Proto-Indo-European language, a suffixed form of (or ), which has given rise to many Indo-European-family words (tens of them defined in English dictionaries) that involve, or stem from, concepts of fiveness. The thumb shares the following with each of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Support (mathematics)
In mathematics, the support of a real-valued function f is the subset of the function domain of elements that are not mapped to zero. If the domain of f is a topological space, then the support of f is instead defined as the smallest closed set containing all points not mapped to zero. This concept is used widely in mathematical analysis. Formulation Suppose that f : X \to \R is a real-valued function whose domain is an arbitrary set X. The of f, written \operatorname(f), is the set of points in X where f is non-zero: \operatorname(f) = \. The support of f is the smallest subset of X with the property that f is zero on the subset's complement. If f(x) = 0 for all but a finite number of points x \in X, then f is said to have . If the set X has an additional structure (for example, a topology), then the support of f is defined in an analogous way as the smallest subset of X of an appropriate type such that f vanishes in an appropriate sense on its complement. The notion of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Schur-convex Function
In mathematics, a Schur-convex function, also known as S-convex, isotonic function and order-preserving function is a function f: \mathbb^d\rightarrow \mathbb that for all x,y\in \mathbb^d such that x is majorized by y, one has that f(x)\le f(y). Named after Issai Schur, Schur-convex functions are used in the study of majorization. A function ''f'' is 'Schur-concave' if its negative, −''f'', is Schur-convex. Properties Every function that is convex and symmetric (under permutations of the arguments) is also Schur-convex. Every Schur-convex function is symmetric, but not necessarily convex. If f is (strictly) Schur-convex and g is (strictly) monotonically increasing, then g\circ f is (strictly) Schur-convex. If g is a convex function defined on a real interval, then \sum_^n g(x_i) is Schur-convex. Schur–Ostrowski criterion If ''f'' is symmetric and all first partial derivatives exist, then ''f'' is Schur-convex if and only if : (x_i - x_j)\left(\frac - \frac\righ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Schur-concave Function
In mathematics, a Schur-convex function, also known as S-convex, isotonic function and order-preserving function is a function f: \mathbb^d\rightarrow \mathbb that for all x,y\in \mathbb^d such that x is majorized by y, one has that f(x)\le f(y). Named after Issai Schur, Schur-convex functions are used in the study of majorization. A function ''f'' is 'Schur-concave' if its negative, −''f'', is Schur-convex. Properties Every function that is convex and symmetric (under permutations of the arguments) is also Schur-convex. Every Schur-convex function is symmetric, but not necessarily convex. If f is (strictly) Schur-convex and g is (strictly) monotonically increasing, then g\circ f is (strictly) Schur-convex. If g is a convex function defined on a real interval, then \sum_^n g(x_i) is Schur-convex. Schur–Ostrowski criterion If ''f'' is symmetric and all first partial derivatives exist, then ''f'' is Schur-convex if and only if : (x_i - x_j)\left(\frac - \frac\ri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |