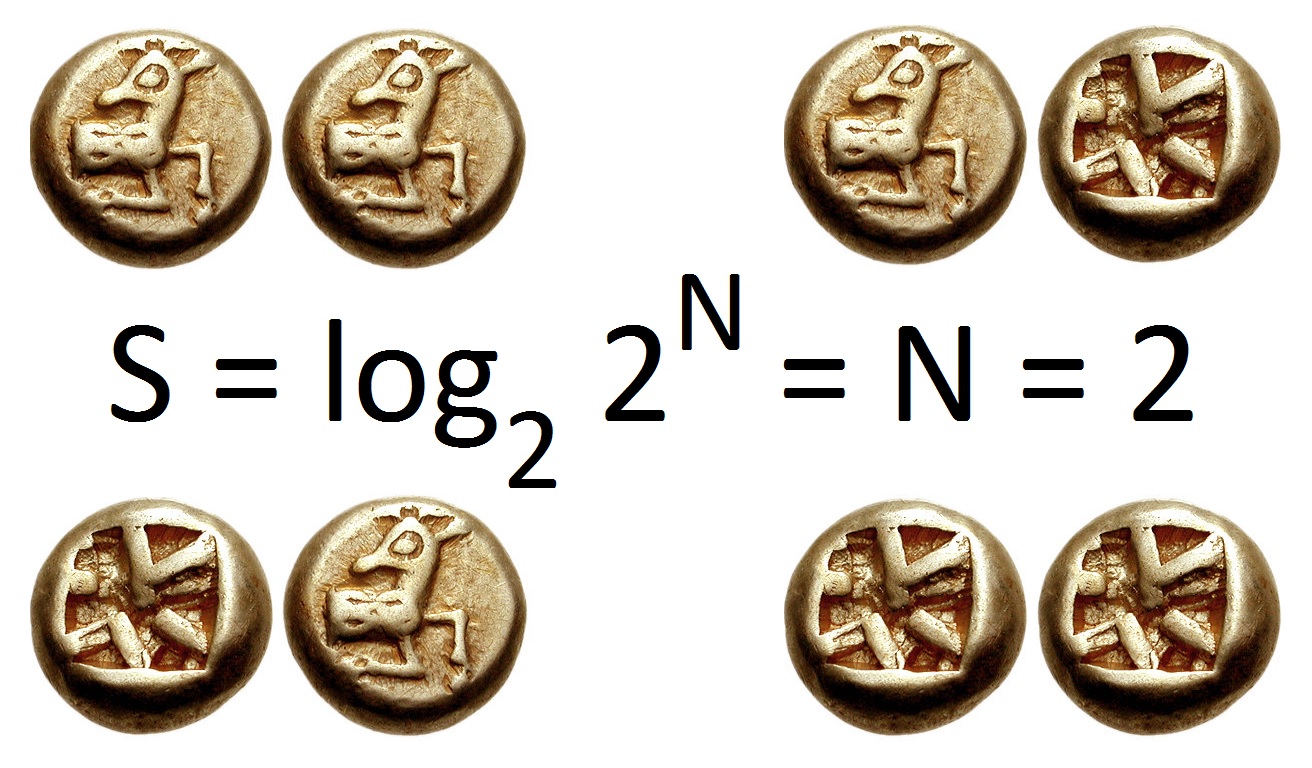|
Shannon (unit)
The shannon (symbol: Sh) is a unit of information named after Claude Shannon, the founder of information theory. IEC 80000-13 defines the shannon as the information content associated with an event when the probability of the event occurring is . It is understood as such within the realm of information theory, and is conceptually distinct from the bit, a term used in data processing and storage to denote a single instance of a binary signal. A sequence of ''n'' binary symbols (such as contained in computer memory or a binary data transmission) is properly described as consisting of ''n'' bits, but the information content of those ''n'' symbols may be more or less than ''n'' shannons depending on the ''a priori'' probability of the actual sequence of symbols. The shannon also serves as a unit of the information entropy of an event, which is defined as the expected value of the information content of the event (i.e., the probability-weighted average of the information content of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantities Of Information
The mathematical theory of information is based on probability theory and statistics, and measures information with several quantities of information. The choice of logarithmic base in the following formulae determines the unit of information entropy that is used. The most common unit of information is the ''bit'', or more correctly the shannon, based on the binary logarithm. Although ''bit'' is more frequently used in place of ''shannon'', its name is not distinguished from the bit as used in data processing to refer to a binary value or stream regardless of its entropy (information content). Other units include the nat, based on the natural logarithm, and the hartley, based on the base 10 or common logarithm. In what follows, an expression of the form p \log p \, is considered by convention to be equal to zero whenever p is zero. This is justified because \lim_ p \log p = 0 for any logarithmic base. Self-information Shannon derived a measure of information content cal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy (information Theory)
In information theory, the entropy of a random variable quantifies the average level of uncertainty or information associated with the variable's potential states or possible outcomes. This measures the expected amount of information needed to describe the state of the variable, considering the distribution of probabilities across all potential states. Given a discrete random variable X, which may be any member x within the set \mathcal and is distributed according to p\colon \mathcal\to[0, 1], the entropy is \Eta(X) := -\sum_ p(x) \log p(x), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or "shannon (unit), shannons"), while base Euler's number, ''e'' gives "natural units" nat (unit), nat, and base 10 gives units of "dits", "bans", or "Hartley (unit), hartleys". An equivalent definition of entropy is the expected value of the self-information of a v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
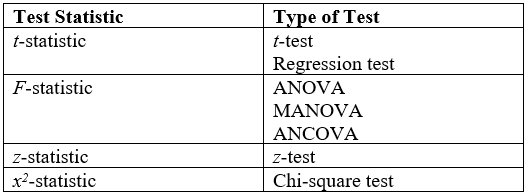
Hypothesis Test
A statistical hypothesis test is a method of statistical inference used to decide whether the data provide sufficient evidence to reject a particular hypothesis. A statistical hypothesis test typically involves a calculation of a test statistic. Then a decision is made, either by comparing the test statistic to a critical value or equivalently by evaluating a ''p''-value computed from the test statistic. Roughly 100 specialized statistical tests are in use and noteworthy. History While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Choice of null hypothesis Paul Meehl has argued that the epistemological importance of the choice of null hypothesis has gone largely unacknowledged. When the null hypothesis is predicted by theory, a more precise experiment will be a more severe test of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal-to-noise Ratio
Signal-to-noise ratio (SNR or S/N) is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. SNR is defined as the ratio of signal power to noise power, often expressed in decibels. A ratio higher than 1:1 (greater than 0 dB) indicates more signal than noise. SNR is an important parameter that affects the performance and quality of systems that process or transmit signals, such as communication systems, audio systems, radar systems, imaging systems, and data acquisition systems. A high SNR means that the signal is clear and easy to detect or interpret, while a low SNR means that the signal is corrupted or obscured by noise and may be difficult to distinguish or recover. SNR can be improved by various methods, such as increasing the signal strength, reducing the noise level, filtering out unwanted noise, or using error correction techniques. SNR also determines the maximum possible amount of data that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Entropy
Differential entropy (also referred to as continuous entropy) is a concept in information theory that began as an attempt by Claude Shannon to extend the idea of (Shannon) entropy (a measure of average surprisal) of a random variable, to continuous probability distributions. Unfortunately, Shannon did not derive this formula, and rather just assumed it was the correct continuous analogue of discrete entropy, but it is not. The actual continuous version of discrete entropy is the limiting density of discrete points (LDDP). Differential entropy (described here) is commonly encountered in the literature, but it is a limiting case of the LDDP, and one that loses its fundamental association with discrete entropy. In terms of measure theory, the differential entropy of a probability measure is the negative relative entropy from that measure to the Lebesgue measure, where the latter is treated as if it were a probability measure, despite being unnormalized. Definition Let X be a rand ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers, sometimes called "the reals", is traditionally denoted by a bold , often using blackboard bold, . The adjective ''real'', used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of . The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers are called irrational numbers. Some irrational numbers (as well as all the rationals) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mutual Information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual Statistical dependence, dependence between the two variables. More specifically, it quantifies the "Information content, amount of information" (in Units of information, units such as shannon (unit), shannons (bits), Nat (unit), nats or Hartley (unit), hartleys) obtained about one random variable by observing the other random variable. The concept of mutual information is intimately linked to that of Entropy (information theory), entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable. Not limited to real-valued random variables and linear dependence like the Pearson correlation coefficient, correlation coefficient, MI is more general and determines how different the joint distribution of the pair (X,Y) is from the product of the marginal distributions of X and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bit Error Rate
In digital transmission, the number of bit errors is the number of received bits of a data stream over a communication channel that have been altered due to noise, interference, distortion or bit synchronization errors. The bit error rate (BER) is the number of bit errors per unit time. The bit error ratio (also BER) is the number of bit errors divided by the total number of transferred bits during a studied time interval. Bit error ratio is a unitless performance measure, often expressed as a percentage. The bit error probability ''pe'' is the expected value of the bit error ratio. The bit error ratio can be considered as an approximate estimate of the bit error probability. This estimate is accurate for a long time interval and a high number of bit errors. Example As an example, assume this transmitted bit sequence: 1 1 0 0 0 1 0 1 1 and the following received bit sequence: 0 1 0 1 0 1 0 0 1, The number of bit errors (the underlined bits) is, in this case, 3. The BER is 3 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coding Theory
Coding theory is the study of the properties of codes and their respective fitness for specific applications. Codes are used for data compression, cryptography, error detection and correction, data transmission and computer data storage, data storage. Codes are studied by various scientific disciplines—such as information theory, electrical engineering, mathematics, linguistics, and computer science—for the purpose of designing efficient and reliable data transmission methods. This typically involves the removal of redundancy and the correction or detection of errors in the transmitted data. There are four types of coding: # Data compression (or ''source coding'') # Error detection and correction, Error control (or ''channel coding'') # Cryptography, Cryptographic coding # Line code, Line coding Data compression attempts to remove unwanted redundancy from the data from a source in order to transmit it more efficiently. For example, DEFLATE data compression makes files small ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
E (mathematical Constant)
The number is a mathematical constant approximately equal to 2.71828 that is the base of a logarithm, base of the natural logarithm and exponential function. It is sometimes called Euler's number, after the Swiss mathematician Leonhard Euler, though this can invite confusion with Euler numbers, or with Euler's constant, a different constant typically denoted \gamma. Alternatively, can be called Napier's constant after John Napier. The Swiss mathematician Jacob Bernoulli discovered the constant while studying compound interest. The number is of great importance in mathematics, alongside 0, 1, Pi, , and . All five appear in one formulation of Euler's identity e^+1=0 and play important and recurring roles across mathematics. Like the constant , is Irrational number, irrational, meaning that it cannot be represented as a ratio of integers, and moreover it is Transcendental number, transcendental, meaning that it is not a root of any non-zero polynomial with rational coefficie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if the base is implicit, simply . Parentheses are sometimes added for clarity, giving , , or . This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity. The natural logarithm of is the exponentiation, power to which would have to be raised to equal . For example, is , because . The natural logarithm of itself, , is , because , while the natural logarithm of is , since . The natural logarithm can be defined for any positive real number as the Integral, area under the curve from to (with the area being negative when ). The simplicity of this definition, which is matched in many other formulas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Common Logarithm
In mathematics, the common logarithm (aka "standard logarithm") is the logarithm with base 10. It is also known as the decadic logarithm, the decimal logarithm and the Briggsian logarithm. The name "Briggsian logarithm" is in honor of the British mathematician Henry Briggs who conceived of and developed the values for the "common logarithm". Historically', the "common logarithm" was known by its Latin name ''logarithmus decimalis'' or ''logarithmus decadis''. The mathematical notation for using the common logarithm is , , or sometimes with a capital ; on calculators, it is printed as "log", but mathematicians usually mean natural logarithm (logarithm with base ≈ 2.71828) rather than common logarithm when writing "log". Before the early 1970s, handheld electronic calculators were not available, and mechanical calculators capable of multiplication were bulky, expensive and not widely available. Instead, tables of base-10 logarithms were used in science, engineering and navi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |