|
Rosetta (orbit)
A Rosetta orbit is a complex type of orbit. In astronomy, a Rosetta orbit occurs when there is a periastron shift during each orbital cycle. A retrograde Newtonian shift can occur when the central mass is extended rather than a point gravitational source, resulting in a non-closed orbit. A prograde relativistic shift happens because of relativistic effects from a massive gravitational source. In barred spiral galaxies with a compact, lens-shaped bar (in contrast with a box-shaped bar), the morphology of the bar is supported by stars following rosette-shaped orbits that rotate with the bar. An object approaching a black hole with an intermediate velocity (not slow enough to spiral into the hole and not fast enough to escape) enters a complex orbit pattern, bounded by a near and far distance to the hole and tracing an oscillating pattern known as a hypotrochoid. In 2020, scientists using observations made by the European Southern Observatory's Very Large Telescope revealed for the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
S2 (star)
S2, also known as S0–2, is a star in the star cluster close to the supermassive black hole Sagittarius A* (Sgr A*), orbiting it with a period of 16.0518 years, a semi-major axis of about 970 au, and a pericenter distance of 17 light hours (18 Tm or 120 au) – an orbit with a period only about 30% longer than that of Jupiter around the Sun, but coming no closer than about four times the distance of Neptune from the Sun. The mass when the star first formed is estimated by the European Southern Observatory (ESO) to have been approximately . Based on its spectral type (B0V ~ B3V), it probably has a mass of 10 to 15 solar masses. Its changing apparent position has been monitored since 1995 by two groups (at UCLA and at the Max Planck Institute for Extraterrestrial Physics) as part of an effort to gather evidence for the existence of a supermassive black hole in the center of the Milky Way galaxy. The accumulating evidence points ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, epitrochoids, hypotrochoids, and involutes. On a basic level, it is the path traced by a curve while rolling on another curve without slipping. Definition Informal definition Roughly speaking, a roulette is the curve described by a point (called the ''generator'' or ''pole'') attached to a given curve as that curve rolls without slipping, along a second given curve that is fixed. More precisely, given a curve attached to a plane which is moving so that the curve rolls, without slipping, along a given curve attached to a fixed plane occupying the same space, then a point attached to the moving plane describes a curve, in the fixed plane called a roulette. Special cases and related concepts In the case where the rolling curve is a line and the generator is a point on the line, the roulette is called an involute of the fixed curve. If the rol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Klemperer Rosette
A Klemperer rosette is a gravitational system of (optionally) alternating heavier and lighter bodies orbiting in a symmetrical pattern around a common barycenter. It was first described by W.B. Klemperer in 1962, and is a special case of a central configuration. Klemperer described rosette systems as follows: The simplest rosette would be a series of four alternating heavier and lighter bodies, 90 degrees from one another, in a rhombic configuration eavy, Light, Heavy, Light where the two larger bodies have the same mass, and likewise the two smaller bodies have the same mass, all orbiting their (empty) geometric center. The more general trojan system has unequal masses for the two heavier bodies, which Klemperer also calls a "rhombic" system, and is the only version that is not symmetric around the gravitational center. The number of "mass types" can be increased, so long as the arrangement is symmetrical and cyclic pattern: e.g. 1,2,3 ... 1,2,3 1,2,3,4,5 ... 1,2,3 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apsidal Precession
In celestial mechanics, apsidal precession (or apsidal advance) is the precession (gradual rotation) of the line connecting the apsis, apsides (line of apsides) of an orbiting body, astronomical body's orbit. The apsides are the orbital points farthest (apoapsis) and closest (periapsis) from its primary (astronomy), primary body. The apsidal precession is the first time derivative of the argument of periapsis, one of the six main orbital elements of an orbit. Apsidal precession is considered positive when the orbit's axis rotates in the same direction as the orbital motion. An apsidal period is the time interval required for an orbit to precess through 360°, which takes the Earth about 112,000 years and the Moon about 8.85 years. History The ancient Greek astronomer Hipparchus noted the apsidal precession of the Moon's orbit (as the revolution of the Moon's apogee with a period of approximately 8.85 years); it is corrected for in the Antikythera Mechanism (circa 80 BC ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
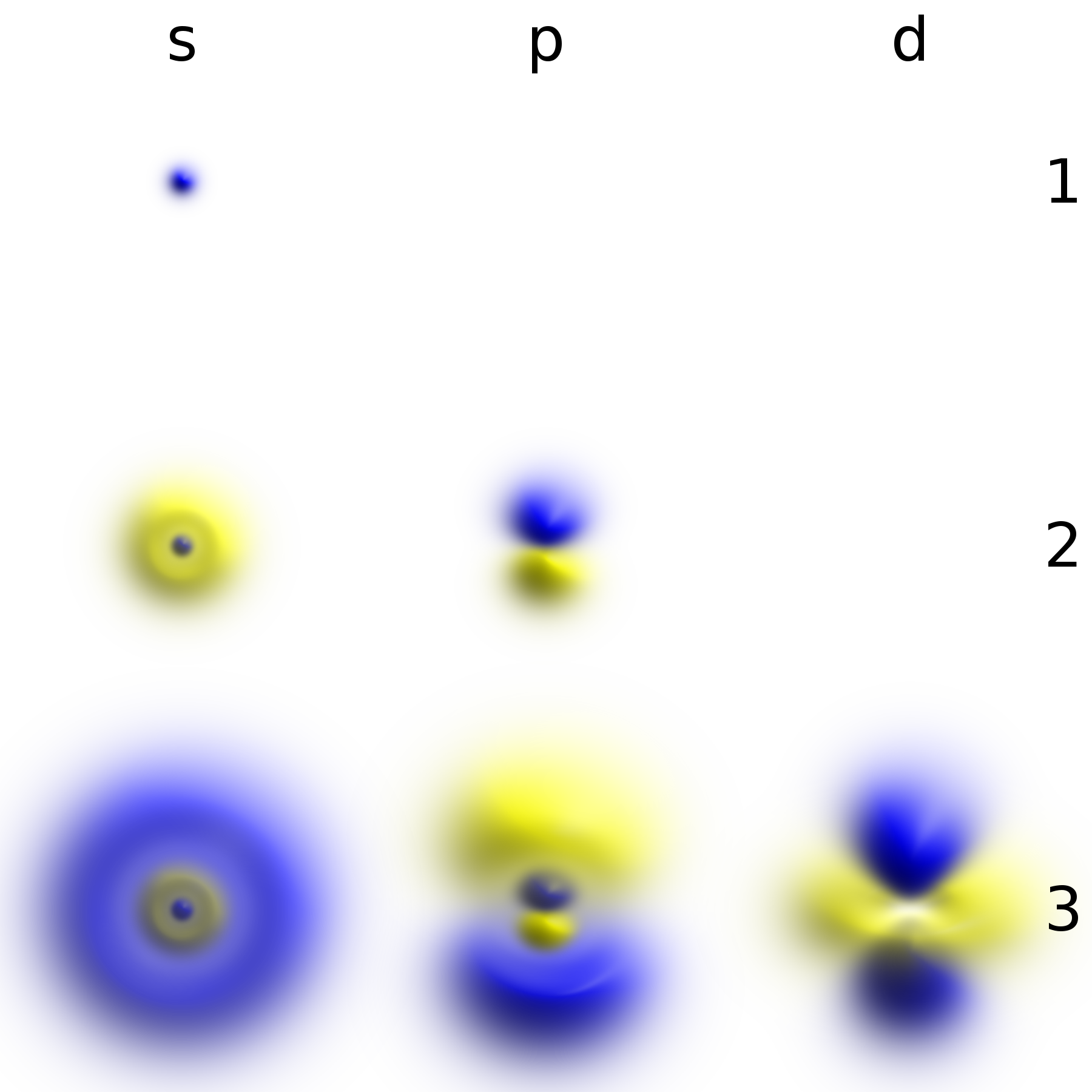
Particle In A Spherically Symmetric Potential
In quantum mechanics, a spherically symmetric potential is a system of which the potential only depends on the radial distance from the spherical center and a location in space. A particle in a spherically symmetric potential will behave accordingly to said potential and can therefore be used as an approximation, for example, of the electron in a hydrogen atom or of the formation of chemical bonds. In the general time-independent case, the dynamics of a particle in a spherically symmetric potential are governed by a Hamiltonian of the following form:\hat = \frac + V() Here, m_0 is the mass of the particle, \hat is the momentum operator, and the potential V(r) depends only on the vector magnitude of the position vector, that is, the radial distance from the origin (hence the spherical symmetry of the problem). To describe a particle in a spherically symmetric system, it is convenient to use spherical coordinates; denoted by r, \theta and \phi. The time-independent Schrödin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sagittarius A*
Sagittarius A*, abbreviated as Sgr A* ( ), is the supermassive black hole at the Galactic Center of the Milky Way. Viewed from Earth, it is located near the border of the constellations Sagittarius and Scorpius, about 5.6° south of the ecliptic, visually close to the Butterfly Cluster (M6) and Lambda Scorpii. Sagittarius A* is a bright and very compact astronomical radio source. In May 2022, astronomers released the first image of the accretion disk around the event horizon of Sagittarius A*, using the Event Horizon Telescope, a world-wide network of radio observatories. This is the second confirmed image of a black hole, after Messier 87's supermassive black hole in 2019. The black hole itself is not seen; as light is incapable of escaping the immense gravitational force of a black hole, only nearby objects whose behavior is influenced by the black hole can be observed. The observed radio and infrared energy emanates from gas and dust heated to millions of d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Very Large Telescope
The Very Large Telescope (VLT) is an astronomical facility operated since 1998 by the European Southern Observatory, located on Cerro Paranal in the Atacama Desert of northern Chile. It consists of four individual telescopes, each equipped with a primary mirror that measures in diameter. These optical telescopes, named ''Antu'', ''Kueyen'', ''Melipal'', and ''Yepun'' (all words for astronomical objects in the Mapuche language), are generally used separately but can be combined to achieve a very high angular resolution. The VLT array is also complemented by four movable Auxiliary Telescopes (ATs) with apertures. The VLT is capable of observing both visible and infrared wavelengths. Each individual telescope can detect objects that are roughly four billion times fainter than what can be seen with the naked eye. When all the telescopes are combined, the facility can achieve an angular resolution of approximately 0.002 arcsecond. In single telescope mode, the angular resol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbit
In celestial mechanics, an orbit (also known as orbital revolution) is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion. For most situations, orbital motion is adequately approximated by Newtonian mechanics, which explains gravity as a force obeying an inverse-square law. However, Albert Einstein's general theory of relativity, which accounts for gravity as due to curvature of spacetime, with orbits following geodesics, provides a more accurate calculation and u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
European Southern Observatory
The European Organisation for Astronomical Research in the Southern Hemisphere, commonly referred to as the European Southern Observatory (ESO), is an intergovernmental organization, intergovernmental research organisation made up of 16 member states for ground-based astronomy. Created in 1962, ESO has provided astronomers with state-of-the-art research facilities and access to the southern sky. The organisation employs over 750 staff members and receives annual member state contributions of approximately €162 million. Its observatories are located in northern Chile. ESO has built and operated some of the largest and most technologically advanced telescopes. These include the 3.6 m New Technology Telescope, an early pioneer in the use of active optics, and the Very Large Telescope (VLT), which consists of four individual 8.2 m telescopes and four smaller auxiliary telescopes which can all work together or separately. The Atacama Large Millimeter Array observes the u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypotrochoid
In geometry, a hypotrochoid is a roulette (curve), roulette traced by a point attached to a circle of radius rolling around the inside of a fixed circle of radius , where the point is a distance from the center of the interior circle. The parametric equations for a hypotrochoid are: :\begin & x (\theta) = (R - r)\cos\theta + d\cos\left(\theta\right) \\ & y (\theta) = (R - r)\sin\theta - d\sin\left(\theta\right) \end where is the angle formed by the horizontal and the center of the rolling circle (these are not polar equations because is not the polar angle). When measured in radian, takes values from 0 to 2 \pi \times \tfrac (where is least common multiple). Special cases include the hypocycloid with and the ellipse with and . The eccentricity of the ellipse is :e=\frac becoming 1 when d=r (see Tusi couple). The classic Spirograph toy traces out hypotrochoid and epitrochoid curves. Hypotrochoids describe the support of the eigenvalues of some random matrices with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |