|
Representations Of Classical Lie Groups
In mathematics, the finite-dimensional representations of the complex classical Lie groups GL(n,\mathbb), SL(n,\mathbb), O(n,\mathbb), SO(n,\mathbb), Sp(2n,\mathbb), can be constructed using the general representation theory of semisimple Lie algebras. The groups SL(n,\mathbb), SO(n,\mathbb), Sp(2n,\mathbb) are indeed simple Lie groups, and their finite-dimensional representations coincide with those of their maximal compact subgroups, respectively SU(n), SO(n), Sp(n). In the classification of simple Lie algebras, the corresponding algebras are : \begin SL(n,\mathbb)&\to A_ \\ SO(n_\text,\mathbb)&\to B_ \\ SO(n_\text) &\to D_ \\ Sp(2n,\mathbb)&\to C_n \end However, since the complex classical Lie groups are linear groups, their representations are tensor representations. Each irreducible representation is labelled by a Young diagram, which encodes its structure and properties. General linear group, special linear group and unitary group Weyl's construction of tensor re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Representation Theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by ''representing'' their elements as linear transformations of vector spaces, and studies modules over these abstract algebraic structures. In essence, a representation makes an abstract algebraic object more concrete by describing its elements by matrices and their algebraic operations (for example, matrix addition, matrix multiplication). The theory of matrices and linear operators is well-understood, so representations of more abstract objects in terms of familiar linear algebra objects helps glean properties and sometimes simplify calculations on more abstract theories. The algebraic objects amenable to such a description include groups, associative algebras and Lie algebras. The most prominent of these (and historically the first) is the representation theory of groups, in which elements of a group are represented by invertible matrices in such a way that the group operation i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group \mathrm_n defined over a finite set of n symbols consists of the permutations that can be performed on the n symbols. Since there are n! (n factorial) such permutation operations, the order (number of elements) of the symmetric group \mathrm_n is n!. Although symmetric groups can be defined on infinite sets, this article focuses on the finite symmetric groups: their applications, their elements, their conjugacy classes, a finite presentation, their subgroups, their automorphism groups, and their representation theory. For the remainder of this article, "symmetric group" will mean a symmetric group on a finite set. The symmetric group is important to diverse areas of mathematics such as Galois theory, invariant theory, the representatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Littlewood–Richardson Rule
In mathematics, the Littlewood–Richardson rule is a combinatorial description of the coefficients that arise when decomposing a product of two Schur functions as a linear combination of other Schur functions. These coefficients are natural numbers, which the Littlewood–Richardson rule describes as counting certain skew tableaux. They occur in many other mathematical contexts, for instance as multiplicity in the decomposition of tensor products of finite-dimensional representations of general linear groups, or in the decomposition of certain induced representations in the representation theory of the symmetric group, or in the area of algebraic combinatorics dealing with Young tableaux and symmetric polynomials. Littlewood–Richardson coefficients depend on three partitions, say \lambda,\mu,\nu, of which \lambda and \mu describe the Schur functions being multiplied, and \nu gives the Schur function of which this is the coefficient in the linear combination; in other words they ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
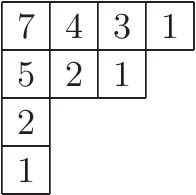
Hook Length Formula
In combinatorial mathematics, the hook length formula is a formula for the number of standard Young tableaux whose shape is a given Young diagram. It has applications in diverse areas such as representation theory, probability, and algorithm analysis; for example, the problem of longest increasing subsequences. A related formula gives the number of semi-standard Young tableaux, which is a specialization of a Schur polynomial. Definitions and statement Let \lambda=(\lambda_1\geq \cdots\geq \lambda_k) be a partition of n=\lambda_1+\cdots+\lambda_k. It is customary to interpret \lambda graphically as a Young diagram, namely a left-justified array of square cells with k rows of lengths \lambda_1,\ldots,\lambda_k. A (standard) Young tableau of shape \lambda is a filling of the n cells of the Young diagram with all the integers \, with no repetition, such that each row and each column form increasing sequences. For the cell in position (i,j), in the ith row and jth column, the hook H_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covering Group
In mathematics, a covering group of a topological group ''H'' is a covering space ''G'' of ''H'' such that ''G'' is a topological group and the covering map is a continuous group homomorphism. The map ''p'' is called the covering homomorphism. A frequently occurring case is a double covering group, a topological double cover in which ''H'' has index 2 in ''G''; examples include the spin groups, pin groups, and metaplectic groups. Roughly explained, saying that for example the metaplectic group Mp2''n'' is a ''double cover'' of the symplectic group Sp2''n'' means that there are always two elements in the metaplectic group representing one element in the symplectic group. Properties Let ''G'' be a covering group of ''H''. The kernel ''K'' of the covering homomorphism is just the fiber over the identity in ''H'' and is a discrete normal subgroup of ''G''. The kernel ''K'' is closed in ''G'' if and only if ''G'' is Hausdorff (and if and only if ''H'' is Hausdorff). Going in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Representation
In the field of representation theory in mathematics, a projective representation of a group ''G'' on a vector space ''V'' over a field ''F'' is a group homomorphism from ''G'' to the projective linear group \mathrm(V) = \mathrm(V) / F^*, where GL(''V'') is the general linear group of invertible linear transformations of ''V'' over ''F'', and ''F''∗ is the normal subgroup consisting of nonzero scalar multiples of the identity transformation (see Scalar transformation). In more concrete terms, a projective representation of G is a collection of operators \rho(g)\in\mathrm(V),\, g\in G satisfying the homomorphism property up to a constant: :\rho(g)\rho(h) = c(g, h)\rho(gh), for some constant c(g, h)\in F. Equivalently, a projective representation of G is a collection of operators \tilde\rho(g)\in\mathrm(V), g\in G, such that \tilde\rho(gh)=\tilde\rho(g)\tilde\rho(h). Note that, in this notation, \tilde\rho(g) is a ''set'' of linear operators related by multiplication with some nonze ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Representations
In mathematics, the spin representations are particular projective representations of the orthogonal or special orthogonal groups in arbitrary dimension and signature (i.e., including indefinite orthogonal groups). More precisely, they are two equivalent representations of the spin groups, which are double covers of the special orthogonal groups. They are usually studied over the real or complex numbers, but they can be defined over other fields. Elements of a spin representation are called spinors. They play an important role in the physical description of fermions such as the electron. The spin representations may be constructed in several ways, but typically the construction involves (perhaps only implicitly) the choice of a maximal isotropic subspace in the vector representation of the group. Over the real numbers, this usually requires using a complexification of the vector representation. For this reason, it is convenient to define the spin representations over the complex n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Group Representation
In mathematics and theoretical physics, a representation of a Lie group is a linear action of a Lie group on a vector space. Equivalently, a representation is a smooth homomorphism of the group into the group of invertible operators on the vector space. Representations play an important role in the study of continuous symmetry. A great deal is known about such representations, a basic tool in their study being the use of the corresponding 'infinitesimal' representations of Lie algebras. Finite-dimensional representations Representations A complex representation of a group is an action by a group on a finite-dimensional vector space over the field \mathbb C. A representation of the Lie group ''G'', acting on an ''n''-dimensional vector space ''V'' over \mathbb C is then a smooth group homomorphism :\Pi:G\rightarrow\operatorname(V), where \operatorname(V) is the general linear group of all invertible linear transformations of V under their composition. Since all ''n''-dimen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Special Orthogonal Group
In mathematics, the orthogonal group in dimension , denoted , is the group of distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of orthogonal matrices, where the group operation is given by matrix multiplication (an orthogonal matrix is a real matrix whose inverse equals its transpose). The orthogonal group is an algebraic group and a Lie group. It is compact. The orthogonal group in dimension has two connected components. The one that contains the identity element is a normal subgroup, called the special orthogonal group, and denoted . It consists of all orthogonal matrices of determinant . This group is also called the rotation group, generalizing the fact that in dimensions 2 and 3, its elements are the usual rotation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal Group
In mathematics, the orthogonal group in dimension , denoted , is the Group (mathematics), group of isometry, distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by Function composition, composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of orthogonal matrix, orthogonal matrices, where the group operation is given by matrix multiplication (an orthogonal matrix is a real matrix whose invertible matrix, inverse equals its transpose). The orthogonal group is an algebraic group and a Lie group. It is compact group, compact. The orthogonal group in dimension has two connected component (topology), connected components. The one that contains the identity element is a normal subgroup, called the special orthogonal group, and denoted . It consists of all orthogonal matrices of determinant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Representation
In mathematics, if is a group and is a linear representation of it on the vector space , then the dual representation is defined over the dual vector space as follows: : is the transpose of , that is, = for all . The dual representation is also known as the contragredient representation. If is a Lie algebra and is a representation of it on the vector space , then the dual representation is defined over the dual vector space as follows: : = for all . The motivation for this definition is that Lie algebra representation associated to the dual of a Lie group representation is computed by the above formula. But the definition of the dual of a Lie algebra representation makes sense even if it does not come from a Lie group representation. In both cases, the dual representation is a representation in the usual sense. Properties Irreducibility and second dual If a (finite-dimensional) representation is irreducible, then the dual representation is also irreducible—but ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.png)