|
Regular Star Polygons
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations on regular simple and star polygons. Branko Grünbaum identified two primary definitions used by Johannes Kepler, one being the regular star polygons with intersecting edges that don't generate new vertices, and the second being simple isotoxal concave polygons. The first usage is included in polygrams which includes polygons like the pentagram but also compound figures like the hexagram. One definition of a ''star polygon'', used in turtle graphics, is a polygon having 2 or more turns (turning number and density), like in spirolaterals.Abelson, Harold, diSessa, Andera, 1980, ''Turtle Geometry'', MIT Press, p.24 Etymology Star polygon names combine a numeral prefix, such as ''penta-'', with the Greek suffix '' -gram'' (in this cas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotoxal
In geometry, a polytope (for example, a polygon or a polyhedron) or a tiling is isotoxal () or edge-transitive if its symmetries act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two edges, there is a translation, rotation, and/or reflection that will move one edge to the other, while leaving the region occupied by the object unchanged. Isotoxal polygons An isotoxal polygon is an even-sided i.e. equilateral polygon, but not all equilateral polygons are isotoxal. The duals of isotoxal polygons are isogonal polygons. Isotoxal 4n-gons are centrally symmetric, so are also zonogons. In general, an isotoxal 2n-gon has \mathrm_n, (^*nn) dihedral symmetry. For example, a rhombus is an isotoxal "2×2-gon" (quadrilateral) with \mathrm_2, (^*22) symmetry. All regular polygons (equilateral triangle, square, etc.) are isotoxal, having double the minimum symmetry order: a regular n-gon has \mathrm_n, (^*nn) dihedral symmetry. An ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
-gram
{{Short pages monitor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greek Language
Greek ( el, label=Modern Greek, Ελληνικά, Elliniká, ; grc, Ἑλληνική, Hellēnikḗ) is an independent branch of the Indo-European family of languages, native to Greece, Cyprus, southern Italy (Calabria and Salento), southern Albania, and other regions of the Balkans, the Black Sea coast, Asia Minor, and the Eastern Mediterranean. It has the longest documented history of any Indo-European language, spanning at least 3,400 years of written records. Its writing system is the Greek alphabet, which has been used for approximately 2,800 years; previously, Greek was recorded in writing systems such as Linear B and the Cypriot syllabary. The alphabet arose from the Phoenician script and was in turn the basis of the Latin, Cyrillic, Armenian, Coptic, Gothic, and many other writing systems. The Greek language holds a very important place in the history of the Western world. Beginning with the epics of Homer, ancient Greek literature includes many works of lasting impo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Penta-
Numeral or number prefixes are prefixes derived from numerals or occasionally other numbers. In English and many other languages, they are used to coin numerous series of words. For example: * unicycle, bicycle, tricycle (1-cycle, 2-cycle, 3-cycle) * dyad, triad (2 parts, 3 parts) * biped, quadruped (2 legs, 4 legs) * September, October, November, December (month 7, month 8, month 9, month 10) * decimal, hexadecimal (base-10, base-16) * septuagenarian, octogenarian (70-79 years old, 80-89 years old) * centipede, millipede (around 100 legs, around 1000 legs) In many European languages there are two principal systems, taken from Latin and Greek, each with several subsystems; in addition, Sanskrit occupies a marginal position. There is also an international set of metric prefixes, which are used in the metric system and which for the most part are either distorted from the forms below or not based on actual number words. Table of number prefixes in English In the following p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numeral Prefix
Numeral or number prefixes are prefixes derived from Numeral (linguistics), numerals or occasionally other numbers. In English and many other languages, they are used to coin numerous series of words. For example: * unicycle, bicycle, tricycle (1-cycle, 2-cycle, 3-cycle) * dyad, triad (2 parts, 3 parts) * biped, quadruped (2 legs, 4 legs) * September, October, November, December (month Julius Caesar, 7, month Augustus, 8, month Septimius Severus, 9, month Octavia E. Butler, 10) * decimal, hexadecimal (base-10, base-16) * septuagenarian, octogenarian (70-79 years old, 80-89 years old) * centipede, millipede (around 100 legs, around 1000 legs) In many European languages there are two principal systems, taken from Latin and Greek language, Greek, each with several subsystems; in addition, Sanskrit occupies a marginal position. There is also an international set of metric prefixes, which are used in the metric system and which for the most part are either distorted from the forms belo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spirolateral
In Euclidean geometry, a spirolateral is a polygon created by a sequence of fixed vertex internal angles and sequential edge lengths 1,2,3,…,''n'' which repeat until the figure closes. The number of repeats needed is called its cycles. Gardner, M. ''Worm Paths'' Ch. 17 ''Knotted Doughnuts and Other Mathematical Entertainments'' New York: W. H. Freeman, pp. 205-221, 1986/ref> A ''simple spirolateral'' has only positive angles. A simple spiral approximates of a portion of an archimedean spiral. A ''general spirolateral'' allows positive and negative angles. A ''spirolateral'' which completes in one turn is a simple polygon, while requiring more than 1 turn is a star polygon and must be self-crossing. A simple spirolateral can be an equangular simple polygon with ''p'' vertices, or an equiangular star polygon with ''p'' vertices and ''q'' turns. Spirolaterals were invented and named by Frank C. Odds as a teenager in 1962, as ''square spirolaterals'' with 90° angles, drawn on gra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density (polygon)
In geometry, the density of a star polyhedron is a generalization of the concept of winding number from two dimensions to higher dimensions, representing the number of windings of the polyhedron around the center of symmetry of the polyhedron. It can be determined by passing a ray from the center to infinity, passing only through the facets of the polytope and not through any lower dimensional features, and counting how many facets it passes through. For polyhedra for which this count does not depend on the choice of the ray, and for which the central point is not itself on any facet, the density is given by this count of crossed facets. The same calculation can be performed for any convex polyhedron, even one without symmetries, by choosing any point interior to the polyhedron as its center. For these polyhedra, the density will be 1. More generally, for any non-self-intersecting (acoptic) polyhedron, the density can be computed as 1 by a similar calculation that chooses ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turning Number
In mathematics, the winding number or winding index of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point, i.e., the curve's number of turns. The winding number depends on the orientation of the curve, and it is negative if the curve travels around the point clockwise. Winding numbers are fundamental objects of study in algebraic topology, and they play an important role in vector calculus, complex analysis, geometric topology, differential geometry, and physics (such as in string theory). Intuitive description Suppose we are given a closed, oriented curve in the ''xy'' plane. We can imagine the curve as the path of motion of some object, with the orientation indicating the direction in which the object moves. Then the winding number of the curve is equal to the total number of counterclockwise turns that the object makes around the origin. When counting the total num ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turn (geometry)
A turn is a unit of plane angle measurement equal to radians, 360 degrees or 400 gradians. Subdivisions of a turn include half-turns, quarter-turns, centiturns, milliturns, etc. The closely related terms ''cycle'' and ''revolution'' are not equivalent to a turn. Subdivisions A turn can be divided in 100 centiturns or milliturns, with each milliturn corresponding to an angle of 0.36°, which can also be written as 21′ 36″. A protractor divided in centiturns is normally called a "percentage protractor". Binary fractions of a turn are also used. Sailors have traditionally divided a turn into 32 compass points, which implicitly have an angular separation of 1/32 turn. The ''binary degree'', also known as the ''binary radian'' (or ''brad''), is turn. The binary degree is used in computing so that an angle can be represented to the maximum possible precision in a single byte. Other measures of angle used in computing may be based on dividin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turtle Graphics
In computer graphics, turtle graphics are vector graphics using a relative cursor (the "turtle") upon a Cartesian plane (x and y axis). Turtle graphics is a key feature of the Logo programming language. Overview The turtle has three attributes: a location, an orientation (or direction), and a pen. The pen, too, has attributes: color, width, and on/off state (also called ''down'' and ''up''). The turtle moves with commands that are relative to its own position, such as "move forward 10 spaces" and "turn left 90 degrees". The pen carried by the turtle can also be controlled, by enabling it, setting its color, or setting its width. A student could understand (and predict and reason about) the turtle's motion by imagining what they would do if they were the turtle. Seymour Papert called this "body syntonic" reasoning. A full turtle graphics system requires control flow, procedures, and recursion: many turtle drawing programs fall short. From these building blocks one can build ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
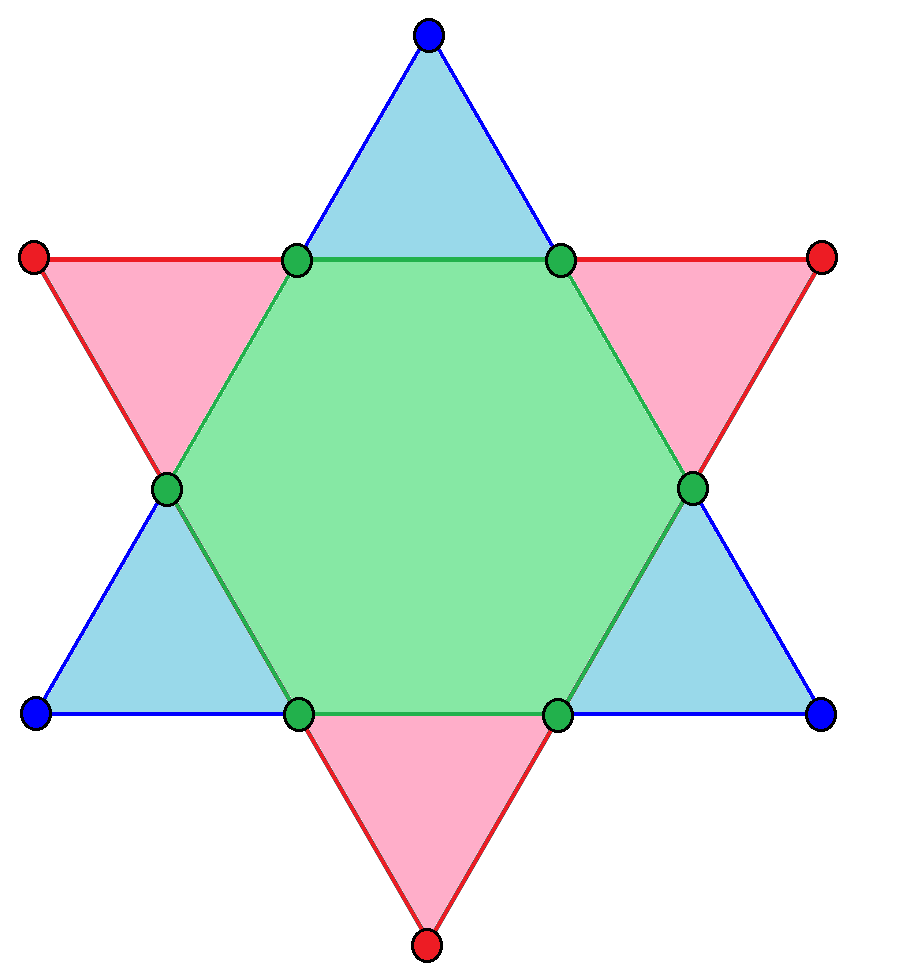
Hexagram
, can be seen as a compound composed of an upwards (blue here) and downwards (pink) facing equilateral triangle, with their intersection as a regular hexagon (in green). A hexagram ( Greek language, Greek) or sexagram (Latin) is a six-pointed geometric star figure with the Schläfli symbol , 2, or . Since there are no true regular continuous hexagrams, the term is instead used to refer to a compound figure of two equilateral triangles. The intersection is a regular hexagon. The hexagram is part of an infinite series of shapes which are compounds of two n-dimensional simplices. In three dimensions, the analogous compound is the stellated octahedron, and in four dimensions the compound of two 5-cells is obtained. It has been historically used in religious and cultural contexts and as decorative motifs. The symbol was used as a decorative motif in medieval Christian churches and Jewish synagogues. It was first used as a mystic symbol by Muslims in the medieval period, known a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |