|
Reduction Strategy (lambda Calculus)
In rewriting, a reduction strategy or rewriting strategy is a relation specifying a rewrite for each object or term, compatible with a given reduction relation. Some authors use the term to refer to an evaluation strategy. Definitions Formally, for an abstract rewriting system (A, \to), a reduction strategy \to_S is a binary relation on A with \to_S \subseteq \overset , where \overset is the transitive closure of \to (but not the reflexive closure). In addition the normal forms of the strategy must be the same as the normal forms of the original rewriting system, i.e. for all a, there exists a b with a\to b iff \exists b'. a\to_S b'. A ''one step'' reduction strategy is one where \to_S \subseteq \to. Otherwise it is a ''many step'' strategy. A ''deterministic'' strategy is one where \to_S is a partial function, i.e. for each a\in A there is at most one b such that a \to_S b. Otherwise it is a ''nondeterministic'' strategy. Term rewriting In a term rewriting system a rewriti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rewriting
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. Such methods may be achieved by rewriting systems (also known as rewrite systems, rewrite engines, or reduction systems). In their most basic form, they consist of a set of objects, plus relations on how to transform those objects. Rewriting can be non-deterministic. One rule to rewrite a term could be applied in many different ways to that term, or more than one rule could be applicable. Rewriting systems then do not provide an algorithm for changing one term to another, but a set of possible rule applications. When combined with an appropriate algorithm, however, rewrite systems can be viewed as computer programs, and several theorem provers and declarative programming languages are based on term rewriting. Example cases Logic In logic, the procedure for obtaining the conjunctive normal form (CNF) of a formula can be implemented as a r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
In-order Traversal
In computer science, tree traversal (also known as tree search and walking the tree) is a form of graph traversal and refers to the process of visiting (e.g. retrieving, updating, or deleting) each node in a tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited. The following algorithms are described for a binary tree, but they may be generalized to other trees as well. Types Unlike linked lists, one-dimensional arrays and other linear data structures, which are canonically traversed in linear order, trees may be traversed in multiple ways. They may be traversed in depth-first or breadth-first order. There are three common ways to traverse them in depth-first order: in-order, pre-order and post-order. Beyond these basic traversals, various more complex or hybrid schemes are possible, such as depth-limited searches like iterative deepening depth-first search. The latter, as well as breadth-first search, can also be us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thunk
In computer programming, a thunk is a subroutine used to inject a calculation into another subroutine. Thunks are primarily used to delay a calculation until its result is needed, or to insert operations at the beginning or end of the other subroutine. They have many other applications in compiler code generation and modular programming. The term originated as a whimsical irregular form of the verb ''think''. It refers to the original use of thunks in ALGOL 60 compilers, which required special analysis (thought) to determine what type of routine to generate. Background The early years of compiler research saw broad experimentation with different evaluation strategies. A key question was how to compile a subroutine call if the arguments can be arbitrary mathematical expressions rather than constants. One approach, known as "call by value", calculates all of the arguments before the call and then passes the resulting values to the subroutine. In the rival "call by name" approach ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reduction Semantics
Operational semantics is a category of formal programming language semantics in which certain desired properties of a program, such as correctness, safety or security, are verified by constructing proofs from logical statements about its execution and procedures, rather than by attaching mathematical meanings to its terms ( denotational semantics). Operational semantics are classified in two categories: structural operational semantics (or small-step semantics) formally describe how the ''individual steps'' of a computation take place in a computer-based system; by opposition natural semantics (or big-step semantics) describe how the ''overall results'' of the executions are obtained. Other approaches to providing a formal semantics of programming languages include axiomatic semantics and denotational semantics. The operational semantics for a programming language describes how a valid program is interpreted as sequences of computational steps. These sequences then ''are'' the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reduction System
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. Such methods may be achieved by rewriting systems (also known as rewrite systems, rewrite engines, or reduction systems). In their most basic form, they consist of a set of objects, plus relations on how to transform those objects. Rewriting can be non-deterministic. One rule to rewrite a term could be applied in many different ways to that term, or more than one rule could be applicable. Rewriting systems then do not provide an algorithm for changing one term to another, but a set of possible rule applications. When combined with an appropriate algorithm, however, rewrite systems can be viewed as computer programs, and several theorem provers and declarative programming languages are based on term rewriting. Example cases Logic In logic, the procedure for obtaining the conjunctive normal form (CNF) of a formula can be implemented as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lazy Evaluation
In programming language theory, lazy evaluation, or call-by-need, is an evaluation strategy which delays the evaluation of an expression until its value is needed ( non-strict evaluation) and which also avoids repeated evaluations ( sharing). The benefits of lazy evaluation include: * The ability to define control flow (structures) as abstractions instead of primitives. * The ability to define potentially infinite data structures. This allows for more straightforward implementation of some algorithms. * The ability to define partially-defined data structures where some elements are errors. This allows for rapid prototyping. Lazy evaluation is often combined with memoization, as described in Jon Bentley's ''Writing Efficient Programs''. After a function's value is computed for that parameter or set of parameters, the result is stored in a lookup table that is indexed by the values of those parameters; the next time the function is called, the table is consulted to determine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
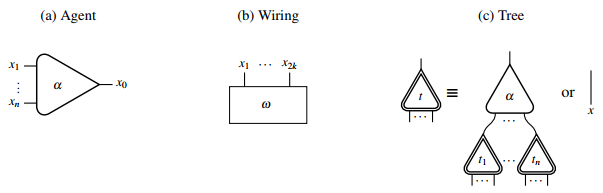
Interaction Nets
Interaction nets are a graphical model of computation devised by Yves Lafont in 1990 as a generalisation of the proof structures of linear logic. An interaction net system is specified by a set of agent types and a set of interaction rules. Interaction nets are an inherently distributed model of computation in the sense that computations can take place simultaneously in many parts of an interaction net, and no synchronisation is needed. The latter is guaranteed by the strong confluence property of reduction in this model of computation. Thus interaction nets provide a natural language for massive parallelism. Interaction nets are at the heart of many implementations of the lambda calculus, such as efficient closed reduction and optimal, in Lévy's sense, Lambdascope. Definitions Interactions nets are graph-like structures consisting of ''agents'' and ''edges''. An agent of type \alpha and with ''arity'' \text(\alpha) = n \ge 0 has one ''principal port'' and n ''auxiliary ports'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barendregt Convention
In mathematical logic, the De Bruijn index is a tool invented by the Dutch mathematician Nicolaas Govert de Bruijn for representing terms of lambda calculus without naming the bound variables. Terms written using these indices are invariant with respect to α-conversion, so the check for α-equivalence is the same as that for syntactic equality. Each De Bruijn index is a natural number that represents an occurrence of a variable in a λ-term, and denotes the number of binders that are in scope between that occurrence and its corresponding binder. The following are some examples: * The term λ''x''. λ''y''. ''x'', sometimes called the K combinator, is written as λ λ 2 with De Bruijn indices. The binder for the occurrence ''x'' is the second λ in scope. * The term λ''x''. λ''y''. λ''z''. ''x'' ''z'' (''y'' ''z'') (the S combinator), with De Bruijn indices, is λ λ λ 3 1 (2 1). * The term λ''z''. (λ''y''. ''y'' (λ''x''. ''x'')) (λ''x''. ''z'' ''x'') is λ (λ 1 (λ 1)) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MIT Press
The MIT Press is a university press affiliated with the Massachusetts Institute of Technology (MIT) in Cambridge, Massachusetts (United States). It was established in 1962. History The MIT Press traces its origins back to 1926 when MIT published under its own name a lecture series entitled ''Problems of Atomic Dynamics'' given by the visiting German physicist and later Nobel Prize winner, Max Born. Six years later, MIT's publishing operations were first formally instituted by the creation of an imprint called Technology Press in 1932. This imprint was founded by James R. Killian, Jr., at the time editor of MIT's alumni magazine and later to become MIT president. Technology Press published eight titles independently, then in 1937 entered into an arrangement with John Wiley & Sons in which Wiley took over marketing and editorial responsibilities. In 1962 the association with Wiley came to an end after a further 125 titles had been published. The press acquired its modern nam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambda Calculus
Lambda calculus (also written as ''λ''-calculus) is a formal system in mathematical logic for expressing computation based on function abstraction and application using variable binding and substitution. It is a universal model of computation that can be used to simulate any Turing machine. It was introduced by the mathematician Alonzo Church in the 1930s as part of his research into the foundations of mathematics. Lambda calculus consists of constructing § lambda terms and performing § reduction operations on them. In the simplest form of lambda calculus, terms are built using only the following rules: * x – variable, a character or string representing a parameter or mathematical/logical value. * (\lambda x.M) – abstraction, function definition (M is a lambda term). The variable x becomes bound in the expression. * (M\ N) – application, applying a function M to an argument N. M and N are lambda terms. The reduction operations include: * (\lambda x.M \rightarrow(\l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pre-order Traversal
In computer science, tree traversal (also known as tree search and walking the tree) is a form of graph traversal and refers to the process of visiting (e.g. retrieving, updating, or deleting) each node in a tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited. The following algorithms are described for a binary tree, but they may be generalized to other trees as well. Types Unlike linked lists, one-dimensional arrays and other linear data structures, which are canonically traversed in linear order, trees may be traversed in multiple ways. They may be traversed in depth-first or breadth-first order. There are three common ways to traverse them in depth-first order: in-order, pre-order and post-order. Beyond these basic traversals, various more complex or hybrid schemes are possible, such as depth-limited searches like iterative deepening depth-first search. The latter, as well as breadth-first search, can also be used to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evaluation Strategy
In a programming language, an evaluation strategy is a set of rules for evaluating expressions. The term is often used to refer to the more specific notion of a ''parameter-passing strategy'' that defines the kind of value that is passed to the function for each parameter (the ''binding strategy'') and whether to evaluate the parameters of a function call, and if so in what order (the ''evaluation order''). The notion of reduction strategy is distinct, although some authors conflate the two terms and the definition of each term is not widely agreed upon. To illustrate, executing a function call f(a,b) may first evaluate the arguments a and b, store the results in references or memory locations ref_a and ref_b, then evaluate the function's body with those references passed in. This gives the function the ability to look up the argument values, to modify them via assignment as if they were local variables, and to return values via the references. This is the call-by-reference eva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |