|
Recurrence Quantification Analysis
Recurrence quantification analysis (RQA) is a method of nonlinear data analysis (cf. chaos theory) for the investigation of dynamical systems. It quantifies the number and duration of recurrences of a dynamical system presented by its phase space trajectory. Background The recurrence quantification analysis (RQA) was developed in order to quantify differently appearing recurrence plots (RPs), based on the small-scale structures therein. Recurrence plots are tools which visualise the recurrence behaviour of the phase space trajectory \vec(i) of dynamical systems: :(i,j) = \Theta(\varepsilon - \, \vec(i) - \vec(j)\, ), where \Theta: \mathbf \rightarrow \ is the Heaviside function and \varepsilon a predefined tolerance. Recurrence plots mostly contain single dots and lines which are parallel to the mean diagonal (''line of identity'', LOI) or which are vertical/horizontal. Lines parallel to the LOI are referred to as ''diagonal lines'' and the vertical structures as ''vertical lines ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists because most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems. Typically, the behavior of a nonlinear system is described in mathematics by a nonlinear system of equations, which is a set of simultaneous equations in which the unknowns (or the unknown functions in the case of differential equations) appear as variables of a polynomial of degree higher than one or in the argument of a function which is not a polynomial of degree one. In other words, in a nonlinear system of equations, the equation(s) to be solved cannot be written as a linear combination of the un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Predictability
Predictability is the degree to which a correct prediction or forecast of a system's state can be made, either qualitatively or quantitatively. Predictability and causality Causal determinism has a strong relationship with predictability. Perfect predictability implies strict determinism, but lack of predictability does not necessarily imply lack of determinism. Limitations on predictability could be caused by factors such as a lack of information or excessive complexity. In experimental physics, there are always observational errors determining variables such as positions and velocities. So perfect prediction is ''practically'' impossible. Moreover, in modern quantum mechanics, Werner Heisenberg's indeterminacy principle puts limits on the accuracy with which such quantities can be known. So such perfect predictability is also ''theoretically'' impossible. Laplace's demon Laplace's demon is a supreme intelligence who could completely predict the one possible future given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
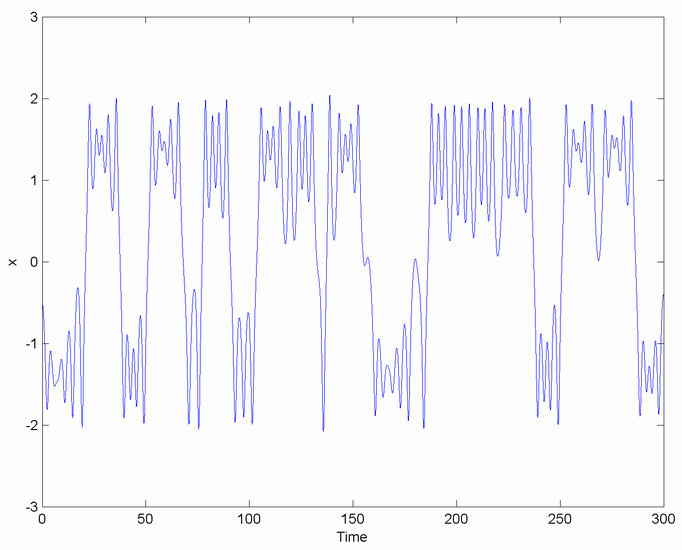
Logistic Map Rqa
Logistic may refer to: Mathematics * Logistic function, a sigmoid function used in many fields ** Logistic map, a recurrence relation that sometimes exhibits chaos ** Logistic regression, a statistical model using the logistic function ** Logit, the inverse of the logistic function ** Logistic distribution, the derivative of the logistic function, a continuous probability distribution, used in probability theory and statistics * Mathematical logic, subfield of mathematics exploring the applications of formal logic to mathematics Other uses * Logistics, the management of resources and their distributions ** Logistic engineering Logistics engineering is a field of engineering dedicated to the scientific organization of the purchase, transport, storage, distribution, and warehousing of materials and finished goods. Logistics engineering is a complex science that conside ..., the scientific study of logistics ** Military logistics, the study of logistics at the service of mili ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Synchronisation
Synchronization is the coordination of events to operate a system in unison. For example, the conductor of an orchestra keeps the orchestra synchronized or ''in time''. Systems that operate with all parts in synchrony are said to be synchronous or ''in sync''—and those that are not are '' asynchronous''. Today, time synchronization can occur between systems around the world through satellite navigation signals and other time and frequency transfer techniques. Navigation and railways Time-keeping and synchronization of clocks is a critical problem in long-distance ocean navigation. Before radio navigation and satellite-based navigation, navigators required accurate time in conjunction with astronomical observations to determine how far east or west their vessel traveled. The invention of an accurate marine chronometer revolutionized marine navigation. By the end of the 19th century, important ports provided time signals in the form of a signal gun, flag, or dropping tim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shannon Entropy
Shannon may refer to: People * Shannon (given name) * Shannon (surname) * Shannon (American singer), stage name of singer Shannon Brenda Greene (born 1958) * Shannon (South Korean singer), British-South Korean singer and actress Shannon Arrum Williams (born 1998) * Shannon, intermittent stage name of English singer-songwriter Marty Wilde (born 1939) * Claude Shannon (1916-2001) was American mathematician, electrical engineer, and cryptographer known as a "father of information theory" Places Australia * Shannon, Tasmania, a locality * Hundred of Shannon, a cadastral unit in South Australia * Shannon, a former name for the area named Calomba, South Australia since 1916 * Shannon River (Western Australia) Canada * Shannon, New Brunswick, a community * Shannon, Quebec, a city * Shannon Bay, former name of Darrell Bay, British Columbia * Shannon Falls, a waterfall in British Columbia Ireland * River Shannon, the longest river in Ireland ** Shannon Cave, a subterranean section o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability
Probability is the branch of mathematics concerning numerical descriptions of how likely an Event (probability theory), event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates impossibility of the event and 1 indicates certainty."Kendall's Advanced Theory of Statistics, Volume 1: Distribution Theory", Alan Stuart and Keith Ord, 6th Ed, (2009), .William Feller, ''An Introduction to Probability Theory and Its Applications'', (Vol 1), 3rd Ed, (1968), Wiley, . The higher the probability of an event, the more likely it is that the event will occur. A simple example is the tossing of a fair (unbiased) coin. Since the coin is fair, the two outcomes ("heads" and "tails") are both equally probable; the probability of "heads" equals the probability of "tails"; and since no other outcomes are possible, the probability of either "heads" or "tails" is 1/2 (which could also be written ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lyapunov Exponent
In mathematics, the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories. Quantitatively, two trajectories in phase space with initial separation vector \delta \mathbf_0 diverge (provided that the divergence can be treated within the linearized approximation) at a rate given by : , \delta\mathbf(t) , \approx e^ , \delta \mathbf_0 , where \lambda is the Lyapunov exponent. The rate of separation can be different for different orientations of initial separation vector. Thus, there is a spectrum of Lyapunov exponents—equal in number to the dimensionality of the phase space. It is common to refer to the largest one as the maximal Lyapunov exponent (MLE), because it determines a notion of predictability for a dynamical system. A positive MLE is usually taken as an indication that the system is chaotic (provided some other conditions are met, e.g., phase space comp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplicative Inverse
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when Multiplication, multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a rational number, fraction ''a''/''b'' is ''b''/''a''. For the multiplicative inverse of a real number, divide 1 by the number. For example, the reciprocal of 5 is one fifth (1/5 or 0.2), and the reciprocal of 0.25 is 1 divided by 0.25, or 4. The reciprocal function, the Function (mathematics), function ''f''(''x'') that maps ''x'' to 1/''x'', is one of the simplest examples of a function which is its own inverse (an Involution (mathematics), involution). Multiplying by a number is the same as Division (mathematics), dividing by its reciprocal and vice versa. For example, multiplication by 4/5 (or 0.8) will give the same result as division by 5/4 (or 1.25). Therefore, multiplication by a number followed by multiplication by its reciprocal yiel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point. As an example, consider air as it is heated or cooled. The velocity of the air at each point defines a vector field. While air is heated in a region, it expands in all directions, and thus the velocity field points outward from that region. The divergence of the velocity field in that region would thus have a positive value. While the air is cooled and thus contracting, the divergence of the velocity has a negative value. Physical interpretation of divergence In physical terms, the divergence of a vector field is the extent to which the vector field flux behaves like a source at a given point. It is a local measure of its "outgoingness" – the extent to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intermittency
In dynamical systems, intermittency is the irregular alternation of phases of apparently periodic and chaotic dynamics ( Pomeau–Manneville dynamics), or different forms of chaotic dynamics (crisis-induced intermittency). Pomeau and Manneville described three routes to intermittency where a nearly periodic system shows irregularly spaced bursts of chaos. These (type I, II and III) correspond to the approach to a saddle-node bifurcation, a subcritical Hopf bifurcation, or an inverse period-doubling bifurcation. In the apparently periodic phases the behaviour is only nearly periodic, slowly drifting away from an unstable periodic orbit. Eventually the system gets far enough away from the periodic orbit to be affected by chaotic dynamics in the rest of the state space, until it gets close to the orbit again and returns to the nearly periodic behaviour. Since the time spent near the periodic orbit depends sensitively on how closely the system entered its vicinity (in turn dete ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laminar Phase
In fluid dynamics, laminar flow is characterized by fluid particles following smooth paths in layers, with each layer moving smoothly past the adjacent layers with little or no mixing. At low velocities, the fluid tends to flow without lateral mixing, and adjacent layers slide past one another like playing cards. There are no cross-currents perpendicular to the direction of flow, nor eddies or swirls of fluids. In laminar flow, the motion of the particles of the fluid is very orderly with particles close to a solid surface moving in straight lines parallel to that surface. Laminar flow is a flow regime characterized by high momentum diffusion and low momentum convection. When a fluid is flowing through a closed channel such as a pipe or between two flat plates, either of two types of flow may occur depending on the velocity and viscosity of the fluid: laminar flow or turbulent flow. Laminar flow occurs at lower velocities, below a threshold at which the flow becomes turbulent. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.svg "Click for more on -> Probability")
.svg "Click for more on -> Divergence")
