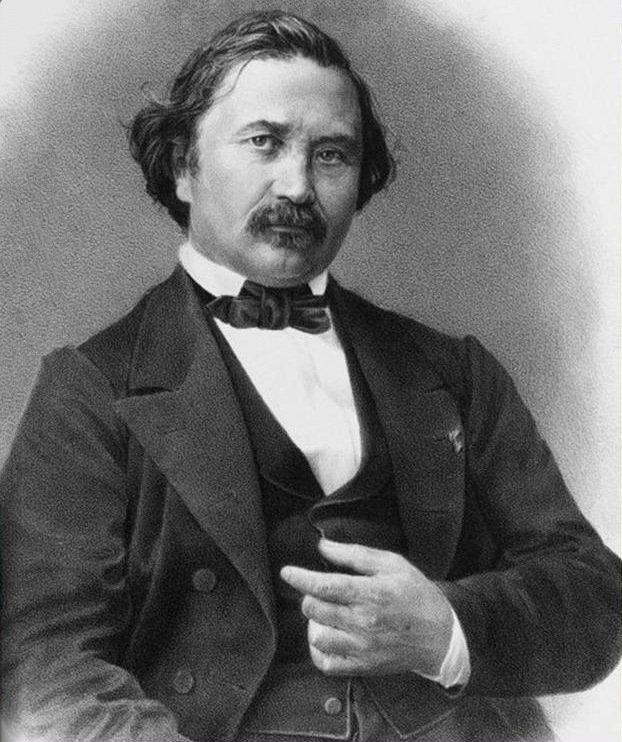|
Ramanujan Prime
In mathematics, a Ramanujan prime is a prime number that satisfies a result proven by Srinivasa Ramanujan relating to the prime-counting function. Origins and definition In 1919, Ramanujan published a new proof of Bertrand's postulate which, as he notes, was first proved by Pafnuty Chebyshev, Chebyshev. At the end of the two-page published paper, Ramanujan derived a generalized result, and that is: : \pi(x) - \pi\left( \frac x 2 \right) \ge 1,2,3,4,5,\ldots \text x \ge 2, 11, 17, 29, 41, \ldots \text where \pi(x) is the prime-counting function, equal to the number of primes less than or equal to ''x''. The converse of this result is the definition of Ramanujan primes: :The ''n''th Ramanujan prime is the least integer ''Rn'' for which \pi(x) - \pi(x/2) \ge n, for all ''x'' ≥ ''Rn''. In other words: Ramanujan primes are the least integers ''Rn'' for which there are at least ''n'' primes between ''x'' and ''x''/2 for all ''x'' ≥ ''Rn''. The firs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number n, called trial division, tests whether n is a multiple of any integer between 2 and \sqrt. Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Srinivasa Ramanujan
Srinivasa Ramanujan (; born Srinivasa Ramanujan Aiyangar, ; 22 December 188726 April 1920) was an Indian mathematician. Though he had almost no formal training in pure mathematics, he made substantial contributions to mathematical analysis, number theory, infinite series, and continued fractions, including solutions to mathematical problems then considered unsolvable. Ramanujan initially developed his own mathematical research in isolation: according to Hans Eysenck: "He tried to interest the leading professional mathematicians in his work, but failed for the most part. What he had to show them was too novel, too unfamiliar, and additionally presented in unusual ways; they could not be bothered". Seeking mathematicians who could better understand his work, in 1913 he began a postal correspondence with the English mathematician G. H. Hardy at the University of Cambridge, England. Recognising Ramanujan's work as extraordinary, Hardy arranged for him to travel to Cambridge. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime-counting Function
In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number ''x''. It is denoted by (''x'') (unrelated to the number ). History Of great interest in number theory is the growth rate of the prime-counting function. It was conjectured in the end of the 18th century by Gauss and by Legendre to be approximately : \frac x where log is the natural logarithm, in the sense that :\lim_ \frac=1. This statement is the prime number theorem. An equivalent statement is :\lim_\pi(x) / \operatorname(x)=1 where li is the logarithmic integral function. The prime number theorem was first proved in 1896 by Jacques Hadamard and by Charles de la Vallée Poussin independently, using properties of the Riemann zeta function introduced by Riemann in 1859. Proofs of the prime number theorem not using the zeta function or complex analysis were found around 1948 by Atle Selberg and by Paul Erdős (for the most part inde ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bertrand's Postulate
In number theory, Bertrand's postulate is a theorem stating that for any integer n > 3, there always exists at least one prime number p with :n < p < 2n - 2. A less restrictive formulation is: for every , there is always at least one prime such that : Another formulation, where is the -th prime, is: for : This statement was first d in 1845 by (1822–1900). Bertrand himself verified his statement for all integers . His conjecture was completely [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pafnuty Chebyshev
Pafnuty Lvovich Chebyshev ( rus, Пафну́тий Льво́вич Чебышёв, p=pɐfˈnutʲɪj ˈlʲvovʲɪtɕ tɕɪbɨˈʂof) ( – ) was a Russian mathematician and considered to be the founding father of Russian mathematics. Chebyshev is known for his fundamental contributions to the fields of probability, statistics, mechanics, and number theory. A number of important mathematical concepts are named after him, including the Chebyshev inequality (which can be used to prove the weak law of large numbers), the Bertrand–Chebyshev theorem, Chebyshev polynomials, Chebyshev linkage, and Chebyshev bias. Transcription The surname Chebyshev has been transliterated in several different ways, like Tchebichef, Tchebychev, Tchebycheff, Tschebyschev, Tschebyschef, Tschebyscheff, Čebyčev, Čebyšev, Chebysheff, Chebychov, Chebyshov (according to native Russian speakers, this one provides the closest pronunciation in English to the correct pronunciation in old Russian), and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asymptotic Analysis
In mathematical analysis, asymptotic analysis, also known as asymptotics, is a method of describing limiting behavior. As an illustration, suppose that we are interested in the properties of a function as becomes very large. If , then as becomes very large, the term becomes insignificant compared to . The function is said to be "''asymptotically equivalent'' to , as ". This is often written symbolically as , which is read as " is asymptotic to ". An example of an important asymptotic result is the prime number theorem. Let denote the prime-counting function (which is not directly related to the constant pi), i.e. is the number of prime numbers that are less than or equal to . Then the theorem states that \pi(x)\sim\frac. Asymptotic analysis is commonly used in computer science as part of the analysis of algorithms and is often expressed there in terms of big O notation. Definition Formally, given functions and , we define a binary relation f(x) \sim g(x) \qu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
International Journal Of Number Theory
International is an adjective (also used as a noun) meaning "between nations". International may also refer to: Music Albums * ''International'' (Kevin Michael album), 2011 * ''International'' (New Order album), 2002 * ''International'' (The Three Degrees album), 1975 *''International'', 2018 album by L'Algérino Songs * The Internationale, the left-wing anthem * "International" (Chase & Status song), 2014 * "International", by Adventures in Stereo from ''Monomania'', 2000 * "International", by Brass Construction from ''Renegades'', 1984 * "International", by Thomas Leer from ''The Scale of Ten'', 1985 * "International", by Kevin Michael from ''International'' (Kevin Michael album), 2011 * "International", by McGuinness Flint from ''McGuinness Flint'', 1970 * "International", by Orchestral Manoeuvres in the Dark from '' Dazzle Ships'', 1983 * "International (Serious)", by Estelle from '' All of Me'', 2012 Politics * Political international, any transnational organization of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |