|
Quantile-parameterized Distribution
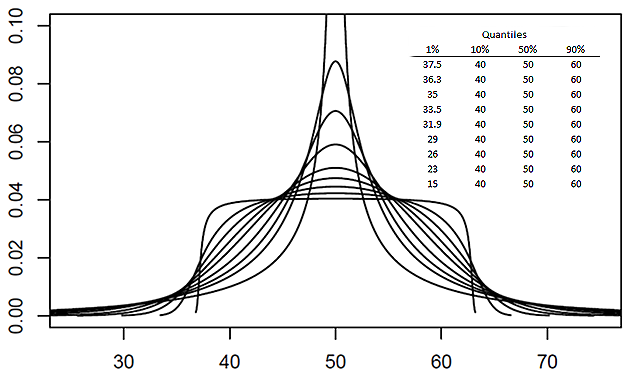
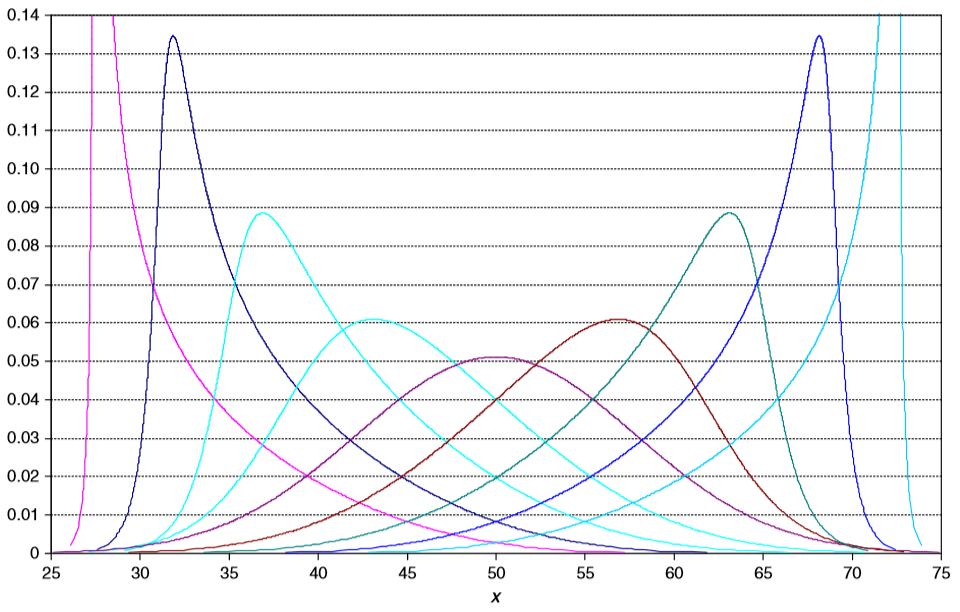
Quantile-parameterized distributions (QPDs) are probability distributions that are directly parameterized by data. They were motivated by the need for easy-to-use continuous probability distributions flexible enough to represent a wide range of uncertainties, such as those commonly encountered in business, economics, engineering, and science. Because QPDs are directly parameterized by data, they have the practical advantage of avoiding the intermediate step of parameter estimation, a time-consuming process that typically requires non-linear iterative methods to estimate probability-distribution parameters from data. Some QPDs have virtually unlimited shape flexibility and closed-form moments as well. History The development of quantile-parameterized distributions was inspired by the practical need for flexible continuous probability distributions that are easy to fit to data. Historically, the Pearson and Johnson families of distributions have been used when shape flexibility is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Estimation Theory
Estimation theory is a branch of statistics that deals with estimating the values of parameters based on measured empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the measured data. An ''estimator'' attempts to approximate the unknown parameters using the measurements. In estimation theory, two approaches are generally considered: * The probabilistic approach (described in this article) assumes that the measured data is random with probability distribution dependent on the parameters of interest * The set-membership approach assumes that the measured data vector belongs to a set which depends on the parameter vector. Examples For example, it is desired to estimate the proportion of a population of voters who will vote for a particular candidate. That proportion is the parameter sought; the estimate is based on a small random sample of voters. Alternatively, it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Optimization
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently, maximizing concave functions over convex sets). Many classes of convex optimization problems admit polynomial-time algorithms, whereas mathematical optimization is in general NP-hard. Convex optimization has applications in a wide range of disciplines, such as automatic control systems, estimation and signal processing, communications and networks, electronic circuit design, data analysis and modeling, finance, statistics ( optimal experimental design), and structural optimization, where the approximation concept has proven to be efficient. With recent advancements in computing and optimization algorithms, convex programming is nearly as straightforward as linear programming. Definition A convex optimization problem is an optimization problem in which the objective function is a convex function and the feasible set is a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of non-deterministic or uncertain processes or measured quantities that may either be single occurrences or evolve over time in a random fashion). Although it is not possible to perfectly predict random events, much can be said about their behavior. Two major results in probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chebyshev Polynomial
The Chebyshev polynomials are two sequences of polynomials related to the cosine and sine functions, notated as T_n(x) and U_n(x). They can be defined in several equivalent ways, one of which starts with trigonometric functions: The Chebyshev polynomials of the first kind T_n are defined by : T_n(\cos \theta) = \cos(n\theta). Similarly, the Chebyshev polynomials of the second kind U_n are defined by : U_n(\cos \theta) \sin \theta = \sin\big((n + 1)\theta\big). That these expressions define polynomials in \cos\theta may not be obvious at first sight, but follows by rewriting \cos(n\theta) and \sin\big((n+1)\theta\big) using de Moivre's formula or by using the angle sum formulas for \cos and \sin repeatedly. For example, the double angle formulas, which follow directly from the angle sum formulas, may be used to obtain T_2(\cos\theta)=\cos(2\theta)=2\cos^2\theta-1 and U_1(\cos\theta)\sin\theta=\sin(2\theta)=2\cos\theta\sin\theta, which are respectively a polynomial in \cos\th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry. Etymology The word ''polynomial'' join ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logistic Distribution
Logistic may refer to: Mathematics * Logistic function, a sigmoid function used in many fields ** Logistic map, a recurrence relation that sometimes exhibits chaos ** Logistic regression, a statistical model using the logistic function ** Logit, the inverse of the logistic function ** Logistic distribution, the derivative of the logistic function, a continuous probability distribution, used in probability theory and statistics * Mathematical logic, subfield of mathematics exploring the applications of formal logic to mathematics Other uses * Logistics, the management of resources and their distributions ** Logistic engineering, the scientific study of logistics ** Military logistics Military logistics is the discipline of planning and carrying out the movement, supply, and maintenance of military forces. In its most comprehensive sense, it is those aspects or military operations that deal with: * Design, development, acqui ..., the study of logistics at the service of milita ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Distribution
The Cauchy distribution, named after Augustin Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as the Lorentz distribution (after Hendrik Lorentz), Cauchy–Lorentz distribution, Lorentz(ian) function, or Breit–Wigner distribution. The Cauchy distribution f(x; x_0,\gamma) is the distribution of the -intercept of a ray issuing from (x_0,\gamma) with a uniformly distributed angle. It is also the distribution of the ratio of two independent normally distributed random variables with mean zero. The Cauchy distribution is often used in statistics as the canonical example of a "pathological" distribution since both its expected value and its variance are undefined (but see below). The Cauchy distribution does not have finite moments of order greater than or equal to one; only fractional absolute moments exist., Chapter 16. The Cauchy distribution has no moment generating function. In mathematics, it is closely related to the P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gumbel Distribution
In probability theory and statistics, the Gumbel distribution (also known as the type-I generalized extreme value distribution) is used to model the distribution of the maximum (or the minimum) of a number of samples of various distributions. This distribution might be used to represent the distribution of the maximum level of a river in a particular year if there was a list of maximum values for the past ten years. It is useful in predicting the chance that an extreme earthquake, flood or other natural disaster will occur. The potential applicability of the Gumbel distribution to represent the distribution of maxima relates to extreme value theory, which indicates that it is likely to be useful if the distribution of the underlying sample data is of the normal or exponential type. ''This article uses the Gumbel distribution to model the distribution of the maximum value''. ''To model the minimum value, use the negative of the original values.'' The Gumbel distribution is a parti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monte Carlo Method
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. Monte Carlo methods are mainly used in three problem classes: optimization, numerical integration, and generating draws from a probability distribution. In physics-related problems, Monte Carlo methods are useful for simulating systems with many coupled degrees of freedom, such as fluids, disordered materials, strongly coupled solids, and cellular structures (see cellular Potts model, interacting particle systems, McKean–Vlasov processes, kinetic models of gases). Other examples include modeling phenomena with significant uncertainty in inputs such as the calculation of ris ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metalog Distribution
The metalog distribution is a flexible continuous probability distribution designed for ease of use in practice. Together with its transforms, the metalog family of continuous distributions is unique because it embodies ''all'' of following properties: virtually unlimited shape flexibility; a choice among unbounded, semi-bounded, and bounded distributions; ease of fitting to data with linear least squares; simple, closed-form quantile function (inverse CDF) equations that facilitate simulation; a simple, closed-form PDF; and Bayesian updating in closed form in light of new data. Moreover, like a Taylor series, metalog distributions may have any number of terms, depending on the degree of shape flexibility desired and other application needs. Applications where metalog distributions can be useful typically involve fitting empirical data, simulated data, or expert-elicited quantiles to smooth, continuous probability distributions. Fields of application are wide-ranging, and incl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Log-normal Distribution
In probability theory, a log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. Thus, if the random variable is log-normally distributed, then has a normal distribution. Equivalently, if has a normal distribution, then the exponential function of , , has a log-normal distribution. A random variable which is log-normally distributed takes only positive real values. It is a convenient and useful model for measurements in exact and engineering sciences, as well as medicine, economics and other topics (e.g., energies, concentrations, lengths, prices of financial instruments, and other metrics). The distribution is occasionally referred to as the Galton distribution or Galton's distribution, after Francis Galton. The log-normal distribution has also been associated with other names, such as McAlister, Gibrat and Cobb–Douglas. A log-normal process is the statistical realization of the multipl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kolmogorov–Smirnov Test
In statistics, the Kolmogorov–Smirnov test (K–S test or KS test) is a nonparametric test of the equality of continuous (or discontinuous, see Section 2.2), one-dimensional probability distributions that can be used to compare a sample with a reference probability distribution (one-sample K–S test), or to compare two samples (two-sample K–S test). In essence, the test answers the question "What is the probability that this collection of samples could have been drawn from that probability distribution?" or, in the second case, "What is the probability that these two sets of samples were drawn from the same (but unknown) probability distribution?". It is named after Andrey Kolmogorov and Nikolai Smirnov. The Kolmogorov–Smirnov statistic quantifies a distance between the empirical distribution function of the sample and the cumulative distribution function of the reference distribution, or between the empirical distribution functions of two samples. The null distributio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |