|
Quantum Inverse Scattering Method
In quantum physics, the quantum inverse scattering method is a method for solving integrable models in 1+1 dimensions, introduced by L. D. Faddeev in 1979. The quantum inverse scattering method relates two different approaches: #the Bethe ansatz, a method of solving integrable quantum models in one space and one time dimension; #the Inverse scattering transform, a method of solving classical integrable differential equations of the evolutionary type. This method led to the formulation of quantum groups. Especially interesting is the Yangian, and the center of the Yangian is given by the quantum determinant. An important concept in the Inverse scattering transform is the Lax representation; the quantum inverse scattering method starts by the quantization of the Lax representation and reproduces the results of the Bethe ansatz. In fact, it allows the Bethe ansatz to be written in a new form: the ''algebraic Bethe ansatz''.cf. e.g. the lectures by N.A. Slavnov, This led to fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Physics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to ho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Schrödinger Equation
In theoretical physics, the (one-dimensional) nonlinear Schrödinger equation (NLSE) is a nonlinear variation of the Schrödinger equation. It is a classical field equation whose principal applications are to the propagation of light in nonlinear optical fibers and planar waveguides and to Bose–Einstein condensates confined to highly anisotropic cigar-shaped traps, in the mean-field regime. Additionally, the equation appears in the studies of small-amplitude gravity waves on the surface of deep inviscid (zero-viscosity) water; the Langmuir waves in hot plasmas; the propagation of plane-diffracted wave beams in the focusing regions of the ionosphere; the propagation of Davydov's alpha-helix solitons, which are responsible for energy transport along molecular chains; and many others. More generally, the NLSE appears as one of universal equations that describe the evolution of slowly varying packets of quasi-monochromatic waves in weakly nonlinear media that have dispersion. Unl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by Henry VIII of England, King Henry VIII in 1534, it is the oldest university press A university press is an academic publishing house specializing in monographs and scholarly journals. Most are nonprofit organizations and an integral component of a large research university. They publish work that has been reviewed by schola ... in the world. It is also the King's Printer. Cambridge University Press is a department of the University of Cambridge and is both an academic and educational publisher. It became part of Cambridge University Press & Assessment, following a merger with Cambridge Assessment in 2021. With a global sales presence, publishing hubs, and offices in more than 40 Country, countries, it publishes over 50,000 titles by authors from over 100 countries. Its publishing includes more than 380 academic journals, monographs, reference works, school and uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Limit
In statistical mechanics, the thermodynamic limit or macroscopic limit, of a system is the limit for a large number of particles (e.g., atoms or molecules) where the volume is taken to grow in proportion with the number of particles.S.J. Blundell and K.M. Blundell, "Concepts in Thermal Physics", Oxford University Press (2009) The thermodynamic limit is defined as the limit of a system with a large volume, with the particle density held fixed. : N \to \infty,\, V \to \infty,\, \frac N V =\text In this limit, macroscopic thermodynamics is valid. There, thermal fluctuations in global quantities are negligible, and all thermodynamic quantities, such as pressure and energy, are simply functions of the thermodynamic variables, such as temperature and density. For example, for a large volume of gas, the fluctuations of the total internal energy are negligible and can be ignored, and the average internal energy can be predicted from knowledge of the pressure and temperature of the gas. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ice-type Model
In statistical mechanics, the ice-type models or six-vertex models are a family of vertex models for crystal lattices with hydrogen bonds. The first such model was introduced by Linus Pauling in 1935 to account for the residual entropy of water ice. Variants have been proposed as models of certain ferroelectric and antiferroelectric crystals. In 1967, Elliott H. Lieb found the exact solution to a two-dimensional ice model known as "square ice". The exact solution in three dimensions is only known for a special "frozen" state. Description An ice-type model is a lattice model defined on a lattice of coordination number 4. That is, each vertex of the lattice is connected by an edge to four "nearest neighbours". A state of the model consists of an arrow on each edge of the lattice, such that the number of arrows pointing inwards at each vertex is 2. This restriction on the arrow configurations is known as the ice rule. In graph theoretic terms, the states are Eulerian orientatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conservation Law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves over time. Exact conservation laws include conservation of energy, conservation of linear momentum, conservation of angular momentum, and conservation of electric charge. There are also many approximate conservation laws, which apply to such quantities as mass, parity, lepton number, baryon number, strangeness, hypercharge, etc. These quantities are conserved in certain classes of physics processes, but not in all. A local conservation law is usually expressed mathematically as a continuity equation, a partial differential equation which gives a relation between the amount of the quantity and the "transport" of that quantity. It states that the amount of the conserved quantity at a point or within a volume can only change by the amount of the quantity which flows in or out of the volume. From Noether's theorem, each conservation la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann–Hilbert Problem
In mathematics, Riemann–Hilbert problems, named after Bernhard Riemann and David Hilbert, are a class of problems that arise in the study of differential equations in the complex plane. Several existence theorems for Riemann–Hilbert problems have been produced by Mark Krein, Israel Gohberg and others (see the book by Clancey and Gohberg (1981)). The Riemann problem Suppose that \Sigma is a closed simple contour in the complex plane dividing the plane into two parts denoted by \Sigma_ (the inside) and \Sigma_ (the outside), determined by the index of the contour with respect to a point. The classical problem, considered in Riemann's PhD dissertation (see ), was that of finding a function :M_+(z) = u(z) + i v(z) analytic inside \Sigma_ such that the boundary values of ''M''+ along \Sigma satisfy the equation :a(z)u(z) - b(z)v(z) = c(z) for all z\in \Sigma, where ''a'', ''b'', and ''c'' are given real-valued functions . By the Riemann mapping theorem, it suffices to consider ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation Function
A correlation function is a function that gives the statistical correlation between random variables, contingent on the spatial or temporal distance between those variables. If one considers the correlation function between random variables representing the same quantity measured at two different points, then this is often referred to as an autocorrelation function, which is made up of autocorrelations. Correlation functions of different random variables are sometimes called cross-correlation functions to emphasize that different variables are being considered and because they are made up of cross-correlations. Correlation functions are a useful indicator of dependencies as a function of distance in time or space, and they can be used to assess the distance required between sample points for the values to be effectively uncorrelated. In addition, they can form the basis of rules for interpolating values at points for which there are no observations. Correlation functions used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
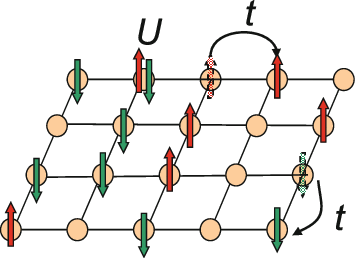
Hubbard Model
The Hubbard model is an approximate model used to describe the transition between conducting and insulating systems. It is particularly useful in solid-state physics. The model is named for John Hubbard. The Hubbard model states that each electron experiences competing forces: one pushes it to tunnel to neighboring atoms, while the other pushes it away from its neighbors. Its Hamiltonian thus has two terms: a kinetic term allowing for tunneling ("hopping") of particles between lattice sites and a potential term reflecting on-site interaction. The particles can either be fermions, as in Hubbard's original work, or bosons, in which case the model is referred to as the "Bose–Hubbard model". The Hubbard model is a useful approximation for particles in a periodic potential at sufficiently low temperatures, where all the particles may be assumed to be in the lowest Bloch band, and long-range interactions between the particles can be ignored. If interactions between particles at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tonks–Girardeau Gas
In physics, a Tonks–Girardeau gas is a Bose gas in which the repulsive interactions between bosonic particles confined to one dimension dominate the system's physics. It is named after physicists Marvin D. Girardeau and Lewi Tonks. It is not a Bose–Einstein condensate as it does not demonstrate any of the necessary characteristics, such as off-diagonal long-range order or a unitary two-body correlation function, even in a thermodynamic limit and as such cannot be described by a macroscopically occupied orbital (order parameter) in the Gross–Pitaevskii formulation. Definition A row of bosons all confined to a one-dimensional line cannot pass each other and therefore cannot exchange places. The resulting motion has been compared to a traffic jam: the motion of each boson is strongly correlated with that of its two neighbors. This can be thought of as the large-''c'' limit of the delta Bose gas. Because the particles cannot exchange places, their behavior might be expected t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lieb–Liniger Model
The Lieb–Liniger model describes a gas of particles moving in one dimension and satisfying Bose–Einstein statistics. Introduction A model of a gas of particles moving in one dimension and satisfying Bose–Einstein statistics was introduced in 1963 Elliott H. Lieb and Werner Liniger, ''Exact Analysis of an Interacting Bose Gas. I. The General Solution and the Ground State'', Physical Review 130: 1605–1616, 1963Elliott H. Lieb, ''Exact Analysis of an Interacting Bose Gas. II. The Excitation Spectrum'', Physical Review 130:1616–1624,1963 in order to study whether the available approximate theories of such gases, specifically Bogoliubov's theory, would conform to the actual properties of the model gas. The model is based on a well defined Schrödinger Hamiltonian for particles interacting with each other via a two-body potential, and all the eigenfunctions and eigenvalues of this Hamiltonian can, in principle, be calculated exactly. Sometimes it is called one dimensional Bose ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heisenberg Model (quantum)
The quantum Heisenberg model, developed by Werner Heisenberg, is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spins of the magnetic systems are treated quantum mechanically. It is related to the prototypical Ising model, where at each site of a lattice, a spin \sigma_i \in \ represents a microscopic magnetic dipole to which the magnetic moment is either up or down. Except the coupling between magnetic dipole moments, there is also a multipolar version of Heisenberg model called the multipolar exchange interaction. Overview For quantum mechanical reasons (see exchange interaction or ), the dominant coupling between two dipoles may cause nearest-neighbors to have lowest energy when they are ''aligned''. Under this assumption (so that magnetic interactions only occur between adjacent dipoles) and on a 1-dimensional periodic lattice, the Hamiltonian can be written in the form :\hat H = -J \sum_^ \sig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
