|
Quantization (linguistics)
In formal semantics, a predicate is quantized if it being true of an entity requires that it is ''not'' true of any proper subparts of that entity. For example, if something is an "apple", then no proper subpart of that thing is an "apple". If something is "water", then many of its subparts will also be "water". Hence, the predicate "apple" is quantized, while "water" is not. Formally, a quantization predicate ''QUA'' can be defined as follows, where U is the universe of discourse, F is a variable over sets, and p is a mereological part structure on U with <_p the mereological part-of : |
Formal Semantics (natural Language)
Formal semantics is the scientific study of linguistic meaning through formal tools from logic and mathematics. It is an interdisciplinary field, sometimes regarded as a subfield of both linguistics and philosophy of language. Formal semanticists rely on diverse methods to analyze natural language. Many examine the meaning of a sentence by studying the circumstances in which it would be true. They describe these circumstances using abstract mathematical models to represent entities and their features. The principle of compositionality helps them link the meaning of expressions to abstract objects in these models. This principle asserts that the meaning of a compound expression is determined by the meanings of its parts. Propositional and predicate logic are formal systems used to analyze the semantic structure of sentences. They introduce concepts like singular terms, predicates, quantifiers, and logical connectives to represent the logical form of natural language expres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
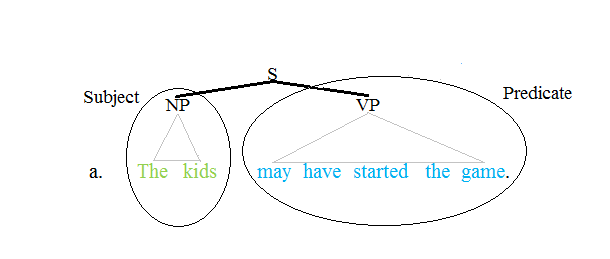
Predicate (grammar)
The term predicate is used in two ways in linguistics and its subfields. The first defines a predicate as everything in a standard declarative sentence except the subject (grammar), subject, and the other defines it as only the main content verb or associated predicative expression of a clause. Thus, by the first definition, the predicate of the sentence ''Frank likes cake'' is ''likes cake'', while by the second definition, it is only the content verb ''likes'', and ''Frank'' and ''cake'' are the argument (linguistics), arguments of this predicate. The conflict between these two definitions can lead to confusion. Syntax Traditional grammar The notion of a predicate in traditional grammar traces back to Aristotelian logic. A predicate is seen as a property that a subject has or is characterized by. A predicate is therefore an expression that can be ''true of'' something. Thus, the expression "is moving" is true of anything that is moving. This classical understanding of pred ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Universe Of Discourse
In the formal sciences, the domain of discourse or universe of discourse (borrowing from the mathematical concept of ''universe'') is the set of entities over which certain variables of interest in some formal treatment may range. It is also defined as the collection of objects being discussed in a specific discourse. In model-theoretical semantics, a universe of discourse is the set of entities that a model is based on. The domain of discourse is usually identified in the preliminaries, so that there is no need in the further treatment to specify each time the range of the relevant variables. Many logicians distinguish, sometimes only tacitly, between the ''domain of a science'' and the ''universe of discourse of a formalization of the science''. Etymology The concept ''universe of discourse'' was used for the first time by George Boole (1854) on page 42 of his '' Laws of Thought'': The concept, probably discovered independently by Boole in 1847, played a crucial role i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set (mathematics)
In mathematics, a set is a collection of different things; the things are '' elements'' or ''members'' of the set and are typically mathematical objects: numbers, symbols, points in space, lines, other geometric shapes, variables, or other sets. A set may be finite or infinite. There is a unique set with no elements, called the empty set; a set with a single element is a singleton. Sets are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the first half of the 20th century. Context Before the end of the 19th century, sets were not studied specifically, and were not clearly distinguished from sequences. Most mathematicians considered infinity as potentialmeaning that it is the result of an endless processand were reluctant to consider infinite sets, that is sets whose number of members is not a natural number. Specific ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mereology
Mereology (; from Greek μέρος 'part' (root: μερε-, ''mere-'') and the suffix ''-logy'', 'study, discussion, science') is the philosophical study of part-whole relationships, also called ''parthood relationships''. As a branch of metaphysics, mereology examines the connections between parts and their wholes, exploring how components interact within a system. This theory has roots in ancient philosophy, with significant contributions from Plato, Aristotle, and later, medieval and Renaissance thinkers like Thomas Aquinas and John Duns Scotus. Mereology was formally axiomatized in the 20th century by Polish logician Stanisław Leśniewski, who introduced it as part of a comprehensive framework for logic and mathematics, and coined the word "mereology". Mereological ideas were influential in early , and formal mereology has continued to be used by a minority in works on the . Different axiomatizations of mereology have been applied in , used in to analyze "mass terms", use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Structure
In mathematics, a structure on a set (or on some sets) refers to providing or endowing it (or them) with certain additional features (e.g. an operation, relation, metric, or topology). Τhe additional features are attached or related to the set (or to the sets), so as to provide it (or them) with some additional meaning or significance. A partial list of possible structures are measures, algebraic structures ( groups, fields, etc.), topologies, metric structures ( geometries), orders, graphs, events, equivalence relations, differential structures, and categories. Sometimes, a set is endowed with more than one feature simultaneously, which allows mathematicians to study the interaction between the different structures more richly. For example, an ordering imposes a rigid form, shape, or topology on the set, and if a set has both a topology feature and a group feature, such that these two features are related in a certain way, then the structure becomes a topological ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relation (mathematics)
In mathematics, a relation denotes some kind of ''relationship'' between two mathematical object, objects in a Set (mathematics), set, which may or may not hold. As an example, "''is less than''" is a relation on the set of natural numbers; it holds, for instance, between the values and (denoted as ), and likewise between and (denoted as ), but not between the values and nor between and , that is, and both evaluate to false. As another example, "''is sister of'' is a relation on the set of all people, it holds e.g. between Marie Curie and Bronisława Dłuska, and likewise vice versa. Set members may not be in relation "to a certain degree" – either they are in relation or they are not. Formally, a relation over a set can be seen as a set of ordered pairs of members of . The relation holds between and if is a member of . For example, the relation "''is less than''" on the natural numbers is an infinite set of pairs of natural numbers that contains both and , b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manfred Krifka
Manfred Krifka (born 26 April 1956 in Dachau) is a German linguist. He was the director of the Leibniz Centre for General Linguistics (Leibniz-Zentrum Allgemeine Sprachwissenschaft, ZAS) in Berlin, and professor of general linguistics at the Humboldt University of Berlin. He was editor of the academic journal ''Linguistics and Philosophy'' from 1999 to 2023 and is editor of ''Theoretical Linguistics'' since 2001. See staff bio and journal web pages in External links below. Career and education Krifka graduated from the Ludwig Maximilian University of Munich in 1986 in Theoretical Linguistics, Philosophy and Theory of Science, and Psycholinguistics. He consequently held positions at the University of Tübingen 1986 - 1989, at the University of Texas at Austin 1990-2000, and at Humboldt University of Berlin 2000 - 2022. Starting in 2001 until November 2022, he has been the director of the Zentrum Allgemeine Sprachwissenschaft (Centre for General Linguistics), since 2017 Leibniz- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Telicity
In linguistics, telicity (; from Greek τέλος "end, goal") is the property of a verb or verb phrase that presents an action or event as having a specific endpoint. A verb or verb phrase with this property is said to be ''telic''; if the situation it describes is ''not'' heading for any particular endpoint, it is said to be ''atelic''. Testing for telicity in English One common way to gauge whether an English language, English verb phrase is telic is to see whether such a phrase as ''in an hour'', in the sense of "within an hour", (known as a ''time-frame adverbial'') can be applied to it. Conversely, a common way to gauge whether the phrase is atelic is to see whether such a phrase as ''for an hour'' (a ''time-span adverbial'') can be applied to it. Defining the relevant notion of "completeness" Having endpoints One often encounters the notion that telic verbs and verb phrases ''refer'' to events that ''have endpoints'', and that atelic ones ''refer'' to events or stat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fewer Vs
''Fewer'' versus ''less'' is a debate in English grammar about the appropriate use of these two determiners. Linguistic prescriptivists usually say that ''fewer'' and not ''less'' should be used with countable nouns, and that ''less'' should be used only with uncountable nouns. This distinction was first tentatively suggested by the grammarian Robert Baker in 1770, and it was eventually presented as a rule by many grammarians since then. However, modern linguistics has shown that idiomatic past and current usage consists of the word ''less'' with both countable nouns and uncountable nouns so that the traditional rule for the use of the word ''fewer'' stands, but not the traditional rule for the use of the word ''less''. As Merriam-Webster's Dictionary of English Usage explains, "''Less'' refers to quantity or amount among things that are measured and to number among things that are counted." Current usage The comparative ''less'' is used with both countable and uncountable no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass Noun
In linguistics, a mass noun, uncountable noun, non-count noun, uncount noun, or just uncountable, is a noun with the syntactic property that any quantity of it is treated as an undifferentiated unit, rather than as something with discrete elements. Uncountable nouns are distinguished from count nouns. Given that different languages have different grammatical features, the actual test for which nouns are mass nouns may vary between languages. In English, mass nouns are characterized by the impossibility of being directly modified by a numeral without specifying a unit of measurement and by the impossibility of being combined with an indefinite article (''a'' or ''an''). Thus, the mass noun "water" is quantified as "20 litres of water" while the count noun "chair" is quantified as "20 chairs". However, both mass and count nouns can be quantified in relative terms without unit specification (e.g., "so much water", "so many chairs", though note the different quantifiers "much" a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mereology
Mereology (; from Greek μέρος 'part' (root: μερε-, ''mere-'') and the suffix ''-logy'', 'study, discussion, science') is the philosophical study of part-whole relationships, also called ''parthood relationships''. As a branch of metaphysics, mereology examines the connections between parts and their wholes, exploring how components interact within a system. This theory has roots in ancient philosophy, with significant contributions from Plato, Aristotle, and later, medieval and Renaissance thinkers like Thomas Aquinas and John Duns Scotus. Mereology was formally axiomatized in the 20th century by Polish logician Stanisław Leśniewski, who introduced it as part of a comprehensive framework for logic and mathematics, and coined the word "mereology". Mereological ideas were influential in early , and formal mereology has continued to be used by a minority in works on the . Different axiomatizations of mereology have been applied in , used in to analyze "mass terms", use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |