|
Pythagorean Comma
In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B (), or D and C. It is equal to the frequency ratio = ≈ 1.01364, or about 23.46 cents, roughly a quarter of a semitone (in between 75:74 and 74:73). The comma that musical temperaments often refer to tempering is the Pythagorean comma. The Pythagorean comma can be also defined as the difference between a Pythagorean apotome and a Pythagorean limma (i.e., between a chromatic and a diatonic semitone, as determined in Pythagorean tuning), or the difference between twelve just perfect fifths and seven octaves, or the difference between three Pythagorean ditones and one octave (this is the reason why the Pythagorean comma is also called a ''ditonic comma''). The diminished second, in Pythagorean tuning, is defined as t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ben Johnston Notation
Benjamin Burwell Johnston Jr. (March 15, 1926 – July 21, 2019) was an American contemporary music composer, known for his use of just intonation. He was called "one of the foremost composers of microtonal music" by Philip Bush and "one of the best non-famous composers this country has to offer" by John Rockwell. Biography Johnston was born in Macon, Georgia, and taught composition and theory at the University of Illinois at Urbana–Champaign from 1951 to 1986, before retiring to North Carolina. During his time teaching, he was in contact with avant-garde figures such as John Cage, La Monte Young, and Iannis Xenakis. Johnston's students have included Stuart Saunders Smith, Neely Bruce, Thomas Albert, Michael Pisaro, Manfred Stahnke, and Kyle Gann. He also considered his practice of just intonation to have influenced other composers, including James Tenney and Larry Polansky. In 1946 he married dance band singer Dorothy Haines, but they soon divorced. In 1950 he married art ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
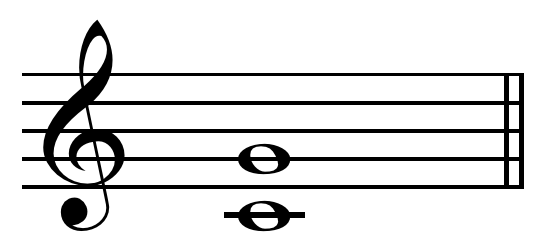
Perfect Fifth
In music theory, a perfect fifth is the musical interval corresponding to a pair of pitches with a frequency ratio of 3:2, or very nearly so. In classical music from Western culture, a fifth is the interval from the first to the last of five consecutive notes in a diatonic scale. The perfect fifth (often abbreviated P5) spans seven semitones, while the diminished fifth spans six and the augmented fifth spans eight semitones. For example, the interval from C to G is a perfect fifth, as the note G lies seven semitones above C. The perfect fifth may be derived from the harmonic series as the interval between the second and third harmonics. In a diatonic scale, the dominant note is a perfect fifth above the tonic note. The perfect fifth is more consonant, or stable, than any other interval except the unison and the octave. It occurs above the root of all major and minor chords (triads) and their extensions. Until the late 19th century, it was often referred to by one of its Gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musical Scale
In music theory, a scale is any set of musical notes ordered by fundamental frequency or pitch. A scale ordered by increasing pitch is an ascending scale, and a scale ordered by decreasing pitch is a descending scale. Often, especially in the context of the common practice period, most or all of the melody and harmony of a musical work is built using the notes of a single scale, which can be conveniently represented on a staff with a standard key signature. Due to the principle of octave equivalence, scales are generally considered to span a single octave, with higher or lower octaves simply repeating the pattern. A musical scale represents a division of the octave space into a certain number of scale steps, a scale step being the recognizable distance (or interval) between two successive notes of the scale. However, there is no need for scale steps to be equal within any scale and, particularly as demonstrated by microtonal music, there is no limit to how many notes can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music," the use of which is "common in most musical systems." The interval between the first and second harmonics of the harmonic series is an octave. In Western music notation, notes separated by an octave (or multiple octaves) have the same name and are of the same pitch class. To emphasize that it is one of the perfect intervals (including unison, perfect fourth, and perfect fifth), the octave is designated P8. Other interval qualities are also possible, though rare. The octave above or below an indicated note is sometimes abbreviated ''8a'' or ''8va'' ( it, all'ottava), ''8va bassa'' ( it, all'ottava bassa, sometimes also ''8vb''), or simply ''8'' for the octave in the direction indicated by plac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Fifth
In music theory, a perfect fifth is the musical interval corresponding to a pair of pitches with a frequency ratio of 3:2, or very nearly so. In classical music from Western culture, a fifth is the interval from the first to the last of five consecutive notes in a diatonic scale. The perfect fifth (often abbreviated P5) spans seven semitones, while the diminished fifth spans six and the augmented fifth spans eight semitones. For example, the interval from C to G is a perfect fifth, as the note G lies seven semitones above C. The perfect fifth may be derived from the harmonic series as the interval between the second and third harmonics. In a diatonic scale, the dominant note is a perfect fifth above the tonic note. The perfect fifth is more consonant, or stable, than any other interval except the unison and the octave. It occurs above the root of all major and minor chords (triads) and their extensions. Until the late 19th century, it was often referred to by one of its Gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Just Intonation
In music, just intonation or pure intonation is the tuning of musical intervals as whole number ratios (such as 3:2 or 4:3) of frequencies. An interval tuned in this way is said to be pure, and is called a just interval. Just intervals (and chords created by combining them) consist of tones from a single harmonic series of an implied fundamental. For example, in the diagram, if the notes G3 and C4 (labelled 3 and 4) are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth. In Western musical practice, instruments are rarely tuned using only pure intervals—the desire for different keys to have identical intervals in Western music makes this impractical. Some instruments of fixed pitch, such as electric pianos, are commonly tuned using equal temperament, in which all intervals other than octaves consist of irrational-number freque ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cuisenaire Rods
Cuisenaire rods are mathematics learning aids for students that provide an interactive, hands-on way to explore mathematics and learn mathematical concepts, such as the four basic arithmetical operations, working with fractions and finding divisors. In the early 1950s, Caleb Gattegno popularised this set of coloured number rods created by Georges Cuisenaire (1891–1975), a Belgan primary school teacher, who called the rods ''réglettes''. According to Gattegno, "Georges Cuisenaire showed in the early 1950s that students who had been taught traditionally, and were rated 'weak', took huge strides when they shifted to using the material. They became 'very good' at traditional arithmetic when they were allowed to manipulate the rods." History The educationalists Maria Montessori and Friedrich Fröbel had used rods to represent numbers, but it was Georges Cuisenaire who introduced the rods that were to be used across the world from the 1950s onwards. In 1952 he published ''Les ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Tone
In Western music theory, a major second (sometimes also called whole tone or a whole step) is a second spanning two semitones (). A second is a musical interval encompassing two adjacent staff positions (see Interval number for more details). For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff positions. Diminished, minor and augmented seconds are notated on adjacent staff positions as well, but consist of a different number of semitones (zero, one, and three). The major second is the interval that occurs between the first and second degrees of a major scale, the tonic and the supertonic. On a musical keyboard, a major second is the interval between two keys separated by one key, counting white and black keys alike. On a guitar string, it is the interval separated by two frets. In moveable-do solfège, it is the interval between ''do'' and ''re''. It is considered a melodi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Third
In classical music, a third is a musical interval encompassing three staff positions (see Interval number for more details), and the major third () is a third spanning four semitones. Forte, Allen (1979). ''Tonal Harmony in Concept and Practice'', p.8. Holt, Rinehart, and Winston. Third edition . "A large 3rd, or ''major 3rd'' (M3) encompassing four half steps." Along with the minor third, the major third is one of two commonly occurring thirds. It is qualified as ''major'' because it is the larger of the two: the major third spans four semitones, the minor third three. For example, the interval from C to E is a major third, as the note E lies four semitones above C, and there are three staff positions from C to E. Diminished and augmented thirds span the same number of staff positions, but consist of a different number of semitones (two and five). The major third may be derived from the harmonic series as the interval between the fourth and fifth harmonics. The maj ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Octave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music," the use of which is "common in most musical systems." The interval between the first and second harmonics of the harmonic series is an octave. In Western music notation, notes separated by an octave (or multiple octaves) have the same name and are of the same pitch class. To emphasize that it is one of the perfect intervals (including unison, perfect fourth, and perfect fifth), the octave is designated P8. Other interval qualities are also possible, though rare. The octave above or below an indicated note is sometimes abbreviated ''8a'' or ''8va'' ( it, all'ottava), ''8va bassa'' ( it, all'ottava bassa, sometimes also ''8vb''), or simply ''8'' for the octave in the direction indicated by placing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Comma
In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B (), or D and C. It is equal to the frequency ratio = ≈ 1.01364, or about 23.46 cents, roughly a quarter of a semitone (in between 75:74 and 74:73). The comma that musical temperaments often refer to tempering is the Pythagorean comma. The Pythagorean comma can be also defined as the difference between a Pythagorean apotome and a Pythagorean limma (i.e., between a chromatic and a diatonic semitone, as determined in Pythagorean tuning), or the difference between twelve just perfect fifths and seven octaves, or the difference between three Pythagorean ditones and one octave (this is the reason why the Pythagorean comma is also called a ''ditonic comma''). The diminished second, in Pythagorean tuning, is defined as t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |