|
Point Group Character Tables
This lists the character tables for the more common molecular point groups used in the study of molecular symmetry. These tables are based on the group-theoretical treatment of the symmetry operations present in common molecules, and are useful in molecular spectroscopy and quantum chemistry. Information regarding the use of the tables, as well as more extensive lists of them, can be found in the references. Notation For each non-linear group, the tables give the most standard notation of the finite group isomorphic to the point group, followed by the order of the group (number of invariant symmetry operations). The finite group notation used is: Zn: cyclic group of order ''n'', Dn: dihedral group isomorphic to the symmetry group of an ''n''–sided regular polygon, Sn: symmetric group on ''n'' letters, and An: alternating group on ''n'' letters. The character tables then follow for all groups. The rows of the character tables correspond to the irreducible representati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Character Table
In group theory, a branch of abstract algebra, a character table is a two-dimensional table whose rows correspond to irreducible representations, and whose columns correspond to conjugacy classes of group (mathematics), group elements. The entries consist of character theory, characters, the trace (linear algebra), traces of the matrix (mathematics), matrices representing group elements of the column's class in the given row's group representation. In chemistry, crystallography, and spectroscopy, List of character tables for chemically important 3D point groups, character tables of point groups are used to classify ''e.g.'' molecule, molecular vibrations according to their symmetry, and to predict whether a transition between two states is forbidden for symmetry reasons. Many university level textbooks on physical chemistry, quantum chemistry, spectroscopy and inorganic chemistry devote a chapter to the use of symmetry group character tables. Definition and example The irreducible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Complex Conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, if a and b are real numbers, then the complex conjugate of a + bi is a - bi. The complex conjugate of z is often denoted as \overline or z^*. In polar form, if r and \varphi are real numbers then the conjugate of r e^ is r e^. This can be shown using Euler's formula. The product of a complex number and its conjugate is a real number: a^2 + b^2 (or r^2 in polar coordinates). If a root of a univariate polynomial with real coefficients is complex, then its complex conjugate is also a root. Notation The complex conjugate of a complex number z is written as \overline z or z^*. The first notation, a vinculum, avoids confusion with the notation for the conjugate transpose of a matrix, which can be thought of as a generalization of the complex conjugate. The second is preferred in physics, where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
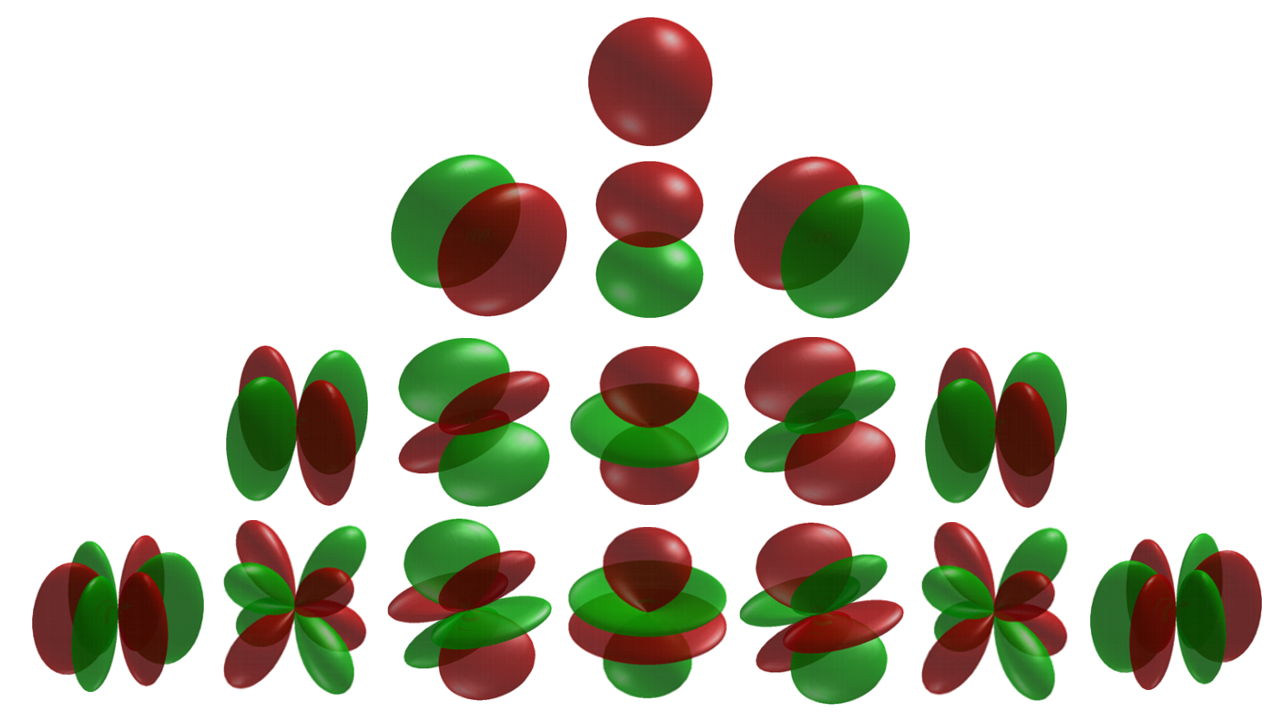
Cubic Harmonic
In fields like computational chemistry and Solid-state physics, solid-state and Condensed matter physics, condensed matter physics the so-called atomic orbitals, or spin-orbitals, as they appear in textbooks on quantum physics, are often partially replaced by cubic harmonics for a number of reasons. These harmonics are usually named tesseral harmonics in the field of condensed matter physics in which the name kubic harmonics rather refers to the irreducible representations in the cubic point-group. Introduction The 2l+1 Hydrogen-like atom, hydrogen-like atomic orbitals with principal quantum number n and angular momentum quantum number l are often expressed as :\psi_(\mathbf) = R_(r) Y_l^m(\theta,\varphi) in which the R_(r) is the radial part of the wave function and Y_l^m(\theta,\varphi) is the angular dependent part. The Y_l^m(\theta,\varphi) are the spherical harmonics, which are solutions of the angular momentum operator. The spherical harmonics are representations of f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
List Of Small Groups
The following list in mathematics contains the finite groups of small order of a group, order up to group isomorphism. Counts For ''n'' = 1, 2, … the number of nonisomorphic groups of order ''n'' is : 1, 1, 1, 2, 1, 2, 1, 5, 2, 2, 1, 5, 1, 2, 1, 14, 1, 5, 1, 5, ... For labeled groups, see . Glossary Each group is named by #Small Groups Library, Small Groups library as G''o''''i'', where ''o'' is the order of the group, and ''i'' is the index used to label the group within that order. Common group names: * Z''n'': the cyclic group of order ''n'' (the notation C''n'' is also used; it is isomorphic to the additive group of Z/''n''Z) * Dih''n'': the dihedral group of order 2''n'' (often the notation D''n'' or D2''n'' is used) ** K4: the Klein four-group of order 4, same as and Dih2 * D2''n'': the dihedral group of order 2''n'', the same as Dih''n'' (notation used in section #List of small non-abelian groups, List of small non-abelian groups) * S''n'': the symmetric group of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
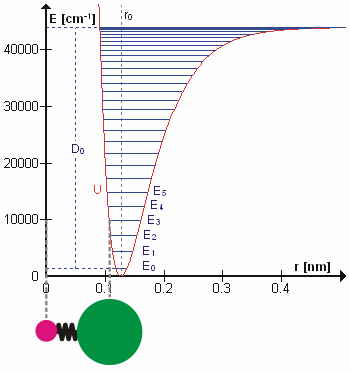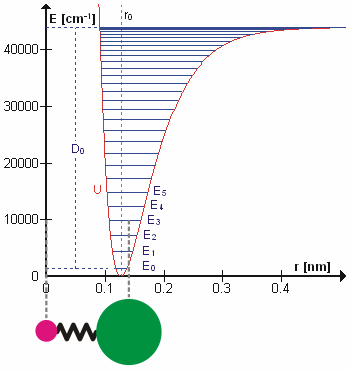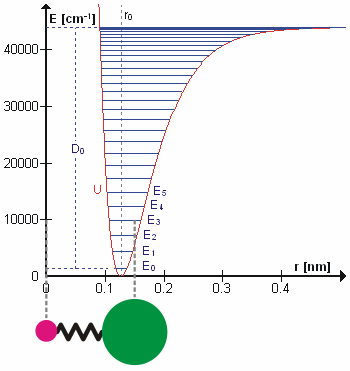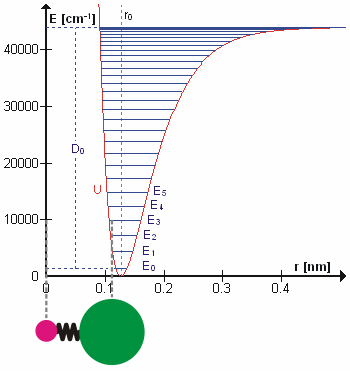
Molecular Vibration
A molecular vibration is a Periodic function, periodic motion of the atoms of a molecule relative to each other, such that the center of mass of the molecule remains unchanged. The infrared spectroscopy correlation table, typical vibrational frequencies range from less than 1013 hertz, Hz to approximately 1014 Hz, corresponding to wavenumbers of approximately 300 to 3000 cm−1 and wavelengths of approximately 30 to 3 μm. Vibrations of polyatomic molecules are described in terms of normal modes, which are independent of each other, but each normal mode involves simultaneous vibrations of parts of the molecule. In general, a non-linear molecule with ''N'' atoms has vibrational mode, normal modes of vibration, but a ''linear'' molecule has modes, because rotation about the molecular axis cannot be observed. A diatomic molecule has one normal mode of vibration, since it can only stretch or compress the single bond. A molecular vibration is excited when the mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Raman Spectroscopy
Raman spectroscopy () (named after physicist C. V. Raman) is a Spectroscopy, spectroscopic technique typically used to determine vibrational modes of molecules, although rotational and other low-frequency modes of systems may also be observed. Raman spectroscopy is commonly used in chemistry to provide a structural fingerprint by which molecules can be identified. Raman spectroscopy relies upon inelastic scattering of photons, known as Raman scattering. A source of monochromatic light, usually from a laser in the visible spectrum, visible, near infrared, or ultraviolet, near ultraviolet range is used, although X-ray Raman scattering, X-rays can also be used. The laser light interacts with molecular vibrations, phonons or other excitations in the system, resulting in the energy of the laser photons being shifted up or down. The shift in energy gives information about the vibrational modes in the system. Time-resolved spectroscopy and infrared spectroscopy typically yields similar y ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Linear Combination Of Atomic Orbitals
A linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In quantum mechanics, electron configurations of atoms are described as wavefunctions. In a mathematical sense, these wave functions are the Basis set (chemistry), basis set of functions, the basis functions, which describe the electrons of a given atom. In chemical reactions, orbital wavefunctions are modified, i.e. the electron cloud shape is changed, according to the type of atoms participating in the chemical bonding, chemical bond. It was introduced in 1929 by Sir John Lennard-Jones with the description of bonding in the diatomic molecules of the first main row of the periodic table, but had been used earlier by Linus Pauling for H2+. Mathematical description An initial assumption is that the number of molecular orbitals is equal to the number of atomic orbitals included in the linear expansion. In a sense, ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Octahedral Symmetry
A regular octahedron has 24 rotational (or orientation-preserving) symmetries, and 48 symmetries altogether. These include transformations that combine a reflection and a rotation. A cube has the same set of symmetries, since it is the polyhedron that is dual polyhedron, dual to an octahedron. The group of orientation-preserving symmetries is S4, the symmetric group or the group of permutations of four objects, since there is exactly one such symmetry for each permutation of the four diagonals of the cube. Details Chiral and full (or achiral) octahedral symmetry are the Point groups in three dimensions, discrete point symmetries (or equivalently, List of spherical symmetry groups, symmetries on the sphere) with the largest symmetry groups compatible with translational symmetry. They are among the Crystal system#Overview of point groups by crystal system, crystallographic point groups of the cubic crystal system. As the hyperoctahedral group of dimension 3 the full octah ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Tetrahedral Group
150px, A regular tetrahedron, an example of a solid with full tetrahedral symmetry A regular tetrahedron has 12 rotational (or orientation-preserving) symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation. The group of all (not necessarily orientation preserving) symmetries is isomorphic to the group S4, the symmetric group of permutations of four objects, since there is exactly one such symmetry for each permutation of the vertices of the tetrahedron. The set of orientation-preserving symmetries forms a group referred to as the alternating subgroup A4 of S4. Details Chiral and full (or achiral tetrahedral symmetry and pyritohedral symmetry) are discrete point symmetries (or equivalently, symmetries on the sphere). They are among the crystallographic point groups of the cubic crystal system. Seen in stereographic projection the edges of the tetrakis hexahedron form 6 circles (or centrally radial lines) in the plane. E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Polyhedral Group
In geometry, the polyhedral groups are the symmetry groups of the Platonic solids. Groups There are three polyhedral groups: *The Tetrahedral symmetry, tetrahedral group of order 12, rotational symmetry group of the tetrahedron, regular tetrahedron. It is isomorphic to Alternating group, A4. ** The conjugacy classes of T are: *** identity *** 4 × rotation by 120°, order 3, cw *** 4 × rotation by 120°, order 3, ccw *** 3 × rotation by 180°, order 2 *The Octahedral symmetry, octahedral group of order 24, rotational symmetry group of the cube and the octahedron, regular octahedron. It is isomorphic to Symmetric group, S4. ** The conjugacy classes of O are: *** identity *** 6 × rotation by ±90° around vertices, order 4 *** 8 × rotation by ±120° around triangle centers, order 3 *** 3 × rotation by 180° around vertices, order 2 *** 6 × rotation by 180° around midpoints of edges, order 2 * The Icosahedral symmetry, icosahedral group of order 60, rotational symmetry group ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Reflection Groups (Cnh)
In group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a reflection group. Reflection groups also include Weyl groups and crystallographic Coxeter groups. While the orthogonal group is generated by reflections (by the Cartan–Dieudonné theorem), it is a continuous group (indeed, Lie group), not a discrete group, and is generally considered separately. Definition Let ''E'' be a finite-dimensional Euclidean space. A finite reflection group is a subgroup of the general linear group of ''E'' which is generated by a set of orthogonal reflections across hyperplanes passing through the origin. An affine reflection group is a discrete subgroup of the affine group of ''E'' that is generated by a set of ''affine reflections'' of ''E'' (without the require ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Pyramidal Groups (Cnv)
A pyramid () is a structure whose visible surfaces are triangular in broad outline and converge toward the top, making the appearance roughly a pyramid in the geometric sense. The base of a pyramid can be of any polygon shape, such as triangular or quadrilateral, and its surface-lines either filled or stepped. A pyramid has the majority of its mass closer to the ground with less mass towards the pyramidion at the apex. This is due to the gradual decrease in the cross-sectional area along the vertical axis with increasing elevation. This offers a weight distribution that allowed early civilizations to create monumental structures.Ancient civilizations in many parts of the world pioneered the building of pyramids. The largest pyramid by volume is the Mesoamerican Great Pyramid of Cholula, in the Mexican state of Puebla. For millennia, the largest structures on Earth were pyramids—first the Red Pyramid in the Dashur Necropolis and then the Great Pyramid of Khufu, both in Egyp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |