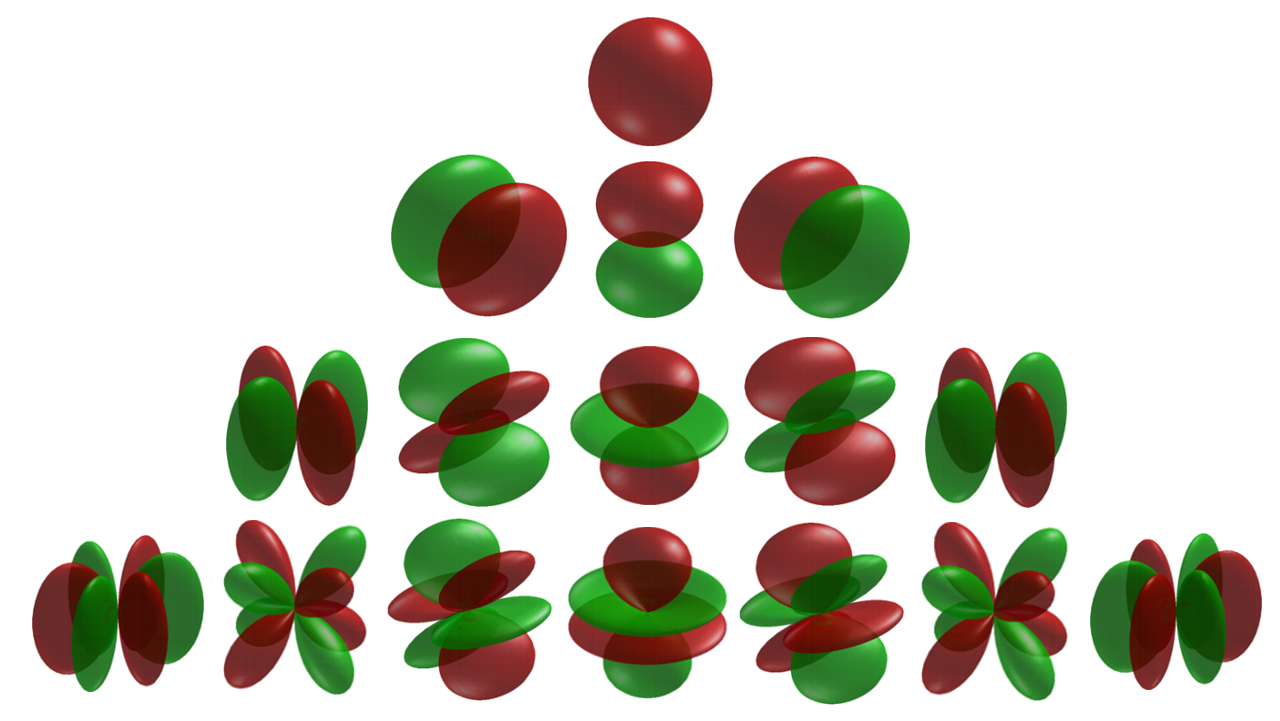
|
Cubic Harmonic
In fields like computational chemistry and solid-state and condensed matter physics the so-called atomic orbitals, or spin-orbitals, as they appear in textbooks on quantum physics, are often partially replaced by cubic harmonics for a number of reasons. These harmonics are usually named tesseral harmonics in the field of condensed matter physics in which the name kubic harmonics rather refers to the irreducible representations in the cubic point-group. Introduction The 2l+1 hydrogen-like atomic orbitals with principal quantum number n and angular momentum quantum number l are often expressed as :\psi_(\mathbf) = R_(r) Y_l^m(\theta,\varphi) in which the R_(r) is the radial part of the wave function and Y_l^m(\theta,\varphi) is the angular dependent part. The Y_l^m(\theta,\varphi) are the spherical harmonics, which are solutions of the angular momentum operator. The spherical harmonics are representations of functions of the full rotation group SO(3) with rotational symme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystal Structure
In crystallography, crystal structure is a description of the ordered arrangement of atoms, ions or molecules in a crystal, crystalline material. Ordered structures occur from the intrinsic nature of the constituent particles to form symmetric patterns that repeat along the principal directions of Three-dimensional space (mathematics), three-dimensional space in matter. The smallest group of particles in the material that constitutes this repeating pattern is the unit cell of the structure. The unit cell completely reflects the symmetry and structure of the entire crystal, which is built up by repetitive Translation (geometry), translation of the unit cell along its principal axes. The translation vectors define the nodes of the Bravais lattice. The lengths of the principal axes, or edges, of the unit cell and the angles between them are the lattice constants, also called ''lattice parameters'' or ''cell parameters''. The symmetry properties of the crystal are described by the con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Space
In mathematics, Hilbert spaces (named after David Hilbert) allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as function spaces. Formally, a Hilbert space is a vector space equipped with an inner product that defines a distance function for which the space is a complete metric space. The earliest Hilbert spaces were studied from this point of view in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer), and ergodic theory (which forms the mathematical underpinning of thermodynamics). John von Neumann coined the term ''Hilbert space'' for the abstract concept that under ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate Vector
In linear algebra, a coordinate vector is a representation of a vector as an ordered list of numbers (a tuple) that describes the vector in terms of a particular ordered basis. An easy example may be a position such as (5, 2, 1) in a 3-dimensional Cartesian coordinate system with the basis as the axes of this system. Coordinates are always specified relative to an ordered basis. Bases and their associated coordinate representations let one realize vector spaces and linear transformations concretely as column vectors, row vectors, and matrices; hence, they are useful in calculations. The idea of a coordinate vector can also be used for infinite-dimensional vector spaces, as addressed below. Definition Let ''V'' be a vector space of dimension ''n'' over a field ''F'' and let : B = \ be an ordered basis for ''V''. Then for every v \in V there is a unique linear combination of the basis vectors that equals '' v '': : v = \alpha _1 b_1 + \alpha _2 b_2 + \cdots + \alpha _n b_n . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthonormal Basis
In mathematics, particularly linear algebra, an orthonormal basis for an inner product space ''V'' with finite dimension is a basis for V whose vectors are orthonormal, that is, they are all unit vectors and orthogonal to each other. For example, the standard basis for a Euclidean space \R^n is an orthonormal basis, where the relevant inner product is the dot product of vectors. The image of the standard basis under a rotation or reflection (or any orthogonal transformation) is also orthonormal, and every orthonormal basis for \R^n arises in this fashion. For a general inner product space V, an orthonormal basis can be used to define normalized orthogonal coordinates on V. Under these coordinates, the inner product becomes a dot product of vectors. Thus the presence of an orthonormal basis reduces the study of a finite-dimensional inner product space to the study of \R^n under dot product. Every finite-dimensional inner product space has an orthonormal basis, which may be ob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tight Binding
In solid-state physics, the tight-binding model (or TB model) is an approach to the calculation of electronic band structure using an approximate set of wave functions based upon superposition of wave functions for isolated atoms located at each atomic site. The method is closely related to the LCAO method (linear combination of atomic orbitals method) used in chemistry. Tight-binding models are applied to a wide variety of solids. The model gives good qualitative results in many cases and can be combined with other models that give better results where the tight-binding model fails. Though the tight-binding model is a one-electron model, the model also provides a basis for more advanced calculations like the calculation of surface states and application to various kinds of many-body problem and quasiparticle calculations. Introduction The name "tight binding" of this electronic band structure model suggests that this quantum mechanical model describes the properties of tightly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Orbital Theory
In chemistry, molecular orbital theory (MO theory or MOT) is a method for describing the electronic structure of molecules using quantum mechanics. It was proposed early in the 20th century. In molecular orbital theory, electrons in a molecule are not assigned to individual chemical bonds between atoms, but are treated as moving under the influence of the atomic nuclei in the whole molecule. Quantum mechanics describes the spatial and energetic properties of electrons as molecular orbitals that surround two or more atoms in a molecule and contain valence electrons between atoms. Molecular orbital theory revolutionized the study of chemical bonding by approximating the states of bonded electrons—the molecular orbitals—as linear combinations of atomic orbitals (LCAO). These approximations are made by applying the density functional theory (DFT) or Hartree–Fock (HF) models to the Schrödinger equation. Molecular orbital theory and valence bond theory are the foundational ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
LCAO
A linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In quantum mechanics, electron configurations of atoms are described as wavefunctions. In a mathematical sense, these wave functions are the basis set of functions, the basis functions, which describe the electrons of a given atom. In chemical reactions, orbital wavefunctions are modified, i.e. the electron cloud shape is changed, according to the type of atoms participating in the chemical bond. It was introduced in 1929 by Sir John Lennard-Jones with the description of bonding in the diatomic molecules of the first main row of the periodic table, but had been used earlier by Linus Pauling for H2+. Mathematical description An initial assumption is that the number of molecular orbitals is equal to the number of atomic orbitals included in the linear expansion. In a sense, ''n'' atomic orbitals combine to for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basis Set (chemistry)
In theoretical and computational chemistry, a basis set is a set of functions (called basis functions) that is used to represent the electronic wave function in the Hartree–Fock method or density-functional theory in order to turn the partial differential equations of the model into algebraic equations suitable for efficient implementation on a computer. The use of basis sets is equivalent to the use of an approximate resolution of the identity: the orbitals , \psi_i\rangle are expanded within the basis set as a linear combination of the basis functions , \psi_i\rangle \approx \sum_\mu c_ , \mu\rangle, where the expansion coefficients c_ are given by c_ = \sum_\nu \langle \mu, \nu \rangle^ \langle \nu , \psi_i \rangle. The basis set can either be composed of atomic orbitals (yielding the linear combination of atomic orbitals approach), which is the usual choice within the quantum chemistry community; plane waves which are typically used within the solid state community, or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomic Orbital
In atomic theory and quantum mechanics, an atomic orbital is a function describing the location and wave-like behavior of an electron in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus. The term ''atomic orbital'' may also refer to the physical region or space where the electron can be calculated to be present, as predicted by the particular mathematical form of the orbital. Each orbital in an atom is characterized by a set of values of the three quantum numbers , , and , which respectively correspond to the electron's energy, angular momentum, and an angular momentum vector component (magnetic quantum number). Alternative to the magnetic quantum number, the orbitals are often labeled by the associated harmonic polynomials (e.g., ''xy'', ). Each such orbital can be occupied by a maximum of two electrons, each with its own projection of spin m_s. The simple names s orbital, p orb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Coordinate System
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the ''radial distance'' of that point from a fixed origin, its ''polar angle'' measured from a fixed zenith direction, and the ''azimuthal angle'' of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane. It can be seen as the three-dimensional version of the polar coordinate system. The radial distance is also called the ''radius'' or ''radial coordinate''. The polar angle may be called '' colatitude'', ''zenith angle'', '' normal angle'', or ''inclination angle''. When radius is fixed, the two angular coordinates make a coordinate system on the sphere sometimes called spherical polar coordinates. The use of symbols and the order of the coordinates differs among sources and disciplines. This article will us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinate System
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference coordinate line is called a ''coordinate axis'' or just ''axis'' (plural ''axes'') of the system, and the point where they meet is its ''origin'', at ordered pair . The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin. One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, ''n'' Cartesian coordinates (an element of real ''n''-space) specify the point in an ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
