|
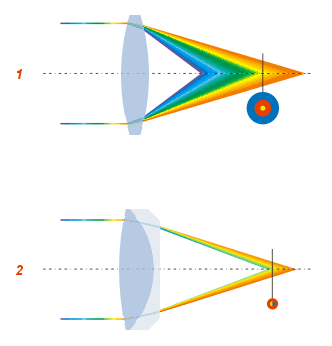
Piston (optics)
In optics, piston is the mean value of a wavefront or phase profile across the pupil of an optical system. The piston coefficient is typically expressed in wavelengths of light at a particular wavelength. Its main use is in curve-fitting wavefronts with Cartesian polynomials or Zernike polynomials. However, similar to a real engine piston moving up and down in its cylinder, optical piston values can be changed to bias the wavefront phase mean value as desired. As phase values can only vary from zero to 2π, then repeat in either direction (termed phase wrapping), changing the piston coefficient changes the zero phase value contour locations across the wavefront. This property is critical to the operation of phase-measuring interferometers, which give not only the magnitude but also the sign (convexity or concavity) of a wavefront under test. Piston is physically created in the interferometer by piezoelectric actuators that translate the Fizeau interferometer reference surfac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviolet, and infrared light. Because light is an electromagnetic wave, other forms of electromagnetic radiation such as X-rays, microwaves, and radio waves exhibit similar properties. Most optical phenomena can be accounted for by using the classical electromagnetic description of light. Complete electromagnetic descriptions of light are, however, often difficult to apply in practice. Practical optics is usually done using simplified models. The most common of these, geometric optics, treats light as a collection of rays that travel in straight lines and bend when they pass through or reflect from surfaces. Physical optics is a more comprehensive model of light, which includes wave effects such as diffraction and interference that cannot be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convexity
Convex or convexity may refer to: Science and technology * Convex lens, in optics Mathematics * Convex set, containing the whole line segment that joins points ** Convex polygon, a polygon which encloses a convex set of points ** Convex polytope, a polytope with a convex set of points ** Convex metric space, a generalization of the convexity notion in abstract metric spaces * Convex function, when the line segment between any two points on the graph of the function lies above or on the graph * Convex conjugate, of a function * Convexity (algebraic geometry), a restrictive technical condition for algebraic varieties originally introduced to analyze Kontsevich moduli spaces Economics and finance * Convexity (finance), second derivatives in financial modeling generally * Convexity in economics * Bond convexity, a measure of the sensitivity of the duration of a bond to changes in interest rates * Convex preferences, an individual's ordering of various outcomes Other uses * Convex Com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane. For curves, the canonical example is that of a circle, which has a curvature equal to the reciprocal of its radius. Smaller circles bend more sharply, and hence have higher curvature. The curvature ''at a point'' of a differentiable curve is the curvature of its osculating circle, that is the circle that best approximates the curve near this point. The curvature of a straight line is zero. In contrast to the tangent, which is a vector quantity, the curvature at a point is typically a scalar quantity, that is, it is expressed by a single real number. For surfaces (and, more generally for higher-dimensional manifolds), that are embedded in a Euclidean space, the concept of curvature is more complex, as it depends on the choice of a direction on the surface or man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aberration (optics)
In optics, aberration is a property of optical systems, such as lenses, that causes light to be spread out over some region of space rather than focused to a point. Aberrations cause the image formed by a lens to be blurred or distorted, with the nature of the distortion depending on the type of aberration. Aberration can be defined as a departure of the performance of an optical system from the predictions of paraxial optics. In an imaging system, it occurs when light from one point of an object does not converge into (or does not diverge from) a single point after transmission through the system. Aberrations occur because the simple paraxial theory is not a completely accurate model of the effect of an optical system on light, rather than due to flaws in the optical elements. An image-forming optical system with aberration will produce an image which is not sharp. Makers of optical instruments need to correct optical systems to compensate for aberration. Aberration can be ana ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tilt (optics)
In optics, tilt is a deviation in the direction a beam of light propagates. Overview Tilt quantifies the average slope in both the X and Y directions of a wavefront or phase profile across the pupil of an optical system. In conjunction with piston (the first Zernike polynomial term), X and Y tilt can be modeled using the second and third Zernike polynomials: :X-Tilt: a_1 \rho \cos(\theta) :Y-Tilt: a_2 \rho \sin(\theta) where \rho is the normalized radius with 0 \le \rho \le 1 and \theta is the azimuthal angle with 0 \le \theta \le 2\pi. The a_1 and a_2 coefficients are typically expressed as a fraction of a chosen wavelength of light. Piston and tilt are not actually true optical aberrations, as they do not represent or model curvature in the wavefront. Defocus is the lowest order true optical aberration. If piston and tilt are subtracted from an otherwise perfect wavefront, a perfect, aberration-free image is formed. Rapid optical tilts in both X and Y directions are t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fizeau Interferometer
A Fizeau interferometerLawson, Peter R. "Principles of Long Baseline Stellar Interferometry." Course notes from the 1999 Michelson Summer School, held August 15–19, 1999. Edited by Peter R. Lawson. Published by National Aeronautics and Space Administration, Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA, 2000. is an interferometric arrangement whereby two reflecting surfaces are placed facing each other. As seen in Fig 1, the rear-surface reflected light from the transparent first reflector is combined with front-surface reflected light from the second reflector to form interference fringes. The term Fizeau interferometer also refers to an interferometric arrangement used by Hippolyte Fizeau in a famous 1851 experiment that seemingly supported the partial ether-drag hypothesis of Augustin Jean Fresnel, but which ultimately played an instrumental role in bringing about a crisis in physics that led to Einstein's development of the theory of special ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Actuators
An actuator is a component of a machine that is responsible for moving and controlling a mechanism or system, for example by opening a valve. In simple terms, it is a "mover". An actuator requires a control device (controlled by control signal) and a source of energy. The control signal is relatively low energy and may be electric voltage or current, pneumatic, or hydraulic fluid pressure, or even human power. Its main energy source may be an electric current, hydraulic pressure, or pneumatic pressure. The Control device is usually a valve. When it receives a control signal, an actuator responds by converting the source's energy into mechanical motion. In the ''electric'', ''hydraulic'', and ''pneumatic'' sense, it is a form of automation or automatic control. History The history of the pneumatic actuation system and the hydraulic actuation system dates to around the time of World War II (1938). It was first created by Xhiter Anckeleman who used his knowledge of engines and brake ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Piezoelectric
Piezoelectricity (, ) is the electric charge that accumulates in certain solid materials—such as crystals, certain ceramics, and biological matter such as bone, DNA, and various proteins—in response to applied Stress (mechanics), mechanical stress. The word ''piezoelectricity'' means electricity resulting from pressure and latent heat. It is derived from the Greek language, Greek word ; ''piezein'', which means to squeeze or press, and ''ēlektron'', which means amber, an ancient source of electric charge. The piezoelectric effect results from the linear electromechanical interaction between the mechanical and electrical states in crystalline materials with no Centrosymmetry, inversion symmetry. The piezoelectric effect is a reversible process (thermodynamics), reversible process: List of piezoelectric materials, materials exhibiting the piezoelectric effect also exhibit the reverse piezoelectric effect, the internal generation of a mechanical strain resulting from an appli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concave
Concave or concavity may refer to: Science and technology * Concave lens * Concave mirror Mathematics * Concave function, the negative of a convex function * Concave polygon, a polygon which is not convex * Concave set * The concavity In calculus, the second derivative, or the second order derivative, of a function is the derivative of the derivative of . Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, ... of a function, determined by its second derivative See also * {{disambiguation, math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Value
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value (magnitude and sign) of a given data set. For a data set, the ''arithmetic mean'', also known as "arithmetic average", is a measure of central tendency of a finite set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the ''sample mean'' (\bar) to distinguish it from the mean, or expected value, of the underlying distribution, the ''population mean'' (denoted \mu or \mu_x).Underhill, L.G.; Bradfield d. (1998) ''Introstat'', Juta and Company Ltd.p. 181/ref> Outside probability and statistics, a wide range of other notions of mean are o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
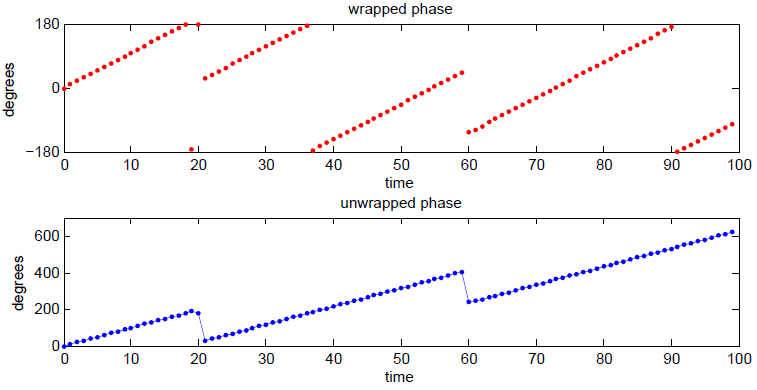
Phase Wrapping
Instantaneous phase and frequency are important concepts in signal processing that occur in the context of the representation and analysis of time-varying functions. The instantaneous phase (also known as local phase or simply phase) of a ''complex-valued'' function ''s''(''t''), is the real-valued function: :\varphi(t) = \arg\, where arg is the complex argument function. The instantaneous frequency is the temporal rate of change of the instantaneous phase. And for a ''real-valued'' function ''s''(''t''), it is determined from the function's analytic representation, ''s''a(''t''): :\begin \varphi(t) &= \arg\ \\ pt &= \arg\, \end where \hat(t) represents the Hilbert transform of ''s''(''t''). When ''φ''(''t'') is constrained to its principal value, either the interval or , it is called ''wrapped phase''. Otherwise it is called ''unwrapped phase'', which is a continuous function of argument ''t'', assuming ''s''a(''t'') is a continuous function of ''t''. Unless ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |