|
Pseudospherical Surface
In geometry, a pseudosphere is a surface with constant negative Gaussian curvature. A pseudosphere of radius is a surface in \mathbb^3 having curvature in each point. Its name comes from the analogy with the sphere of radius , which is a surface of curvature . The term was introduced by Eugenio Beltrami in his 1868 paper on models of hyperbolic geometry. __TOC__ Tractroid The same surface can be also described as the result of revolving a tractrix about its asymptote. For this reason the pseudosphere is also called tractroid. As an example, the (half) pseudosphere (with radius 1) is the surface of revolution of the tractrix parametrized by :t \mapsto \left( t - \tanh, \operatorname\, \right), \quad \quad 0 \le t < \infty. It is a singular space (the equator is a singularity), but away from the singularities, it has constant negative |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a '' geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Saddle Surface
In mathematics, a saddle point or minimax point is a point on the surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a critical point), but which is not a local extremum of the function. An example of a saddle point is when there is a critical point with a relative minimum along one axial direction (between peaks) and at a relative maximum along the crossing axis. However, a saddle point need not be in this form. For example, the function f(x,y) = x^2 + y^3 has a critical point at (0, 0) that is a saddle point since it is neither a relative maximum nor relative minimum, but it does not have a relative maximum or relative minimum in the y-direction. The name derives from the fact that the prototypical example in two dimensions is a surface that ''curves up'' in one direction, and ''curves down'' in a different direction, resembling a riding saddle or a mountain pass between two peaks forming a landform saddle. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minkowski Space
In mathematical physics, Minkowski space (or Minkowski spacetime) () is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Although initially developed by mathematician Hermann Minkowski for Maxwell's equations of electromagnetism, the mathematical structure of Minkowski spacetime was shown to be implied by the postulates of special relativity. Minkowski space is closely associated with Einstein's theories of special relativity and general relativity and is the most common mathematical structure on which special relativity is formulated. While the individual components in Euclidean space and time may differ due to length contraction and time dilation, in Minkowski spacetime, all frames of reference will agree on the total distance in spacetime between events.This makes spacetime distance an invarian ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
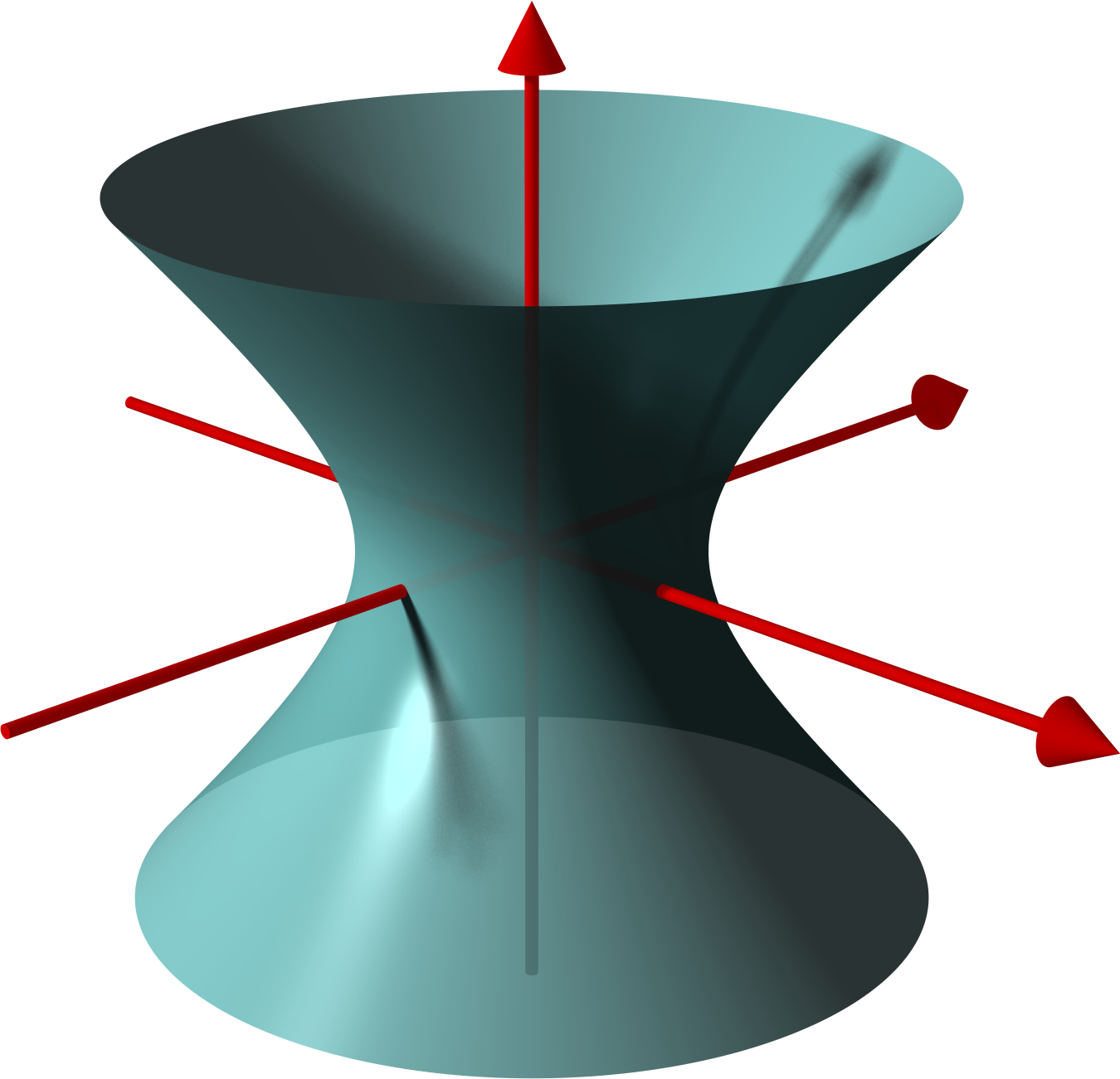
Hyperboloid
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation. A hyperboloid is a quadric surface, that is, a surface defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, a hyperboloid is characterized by not being a cone or a cylinder, having a center of symmetry, and intersecting many planes into hyperbolas. A hyperboloid has three pairwise perpendicular axes of symmetry, and three pairwise perpendicular planes of symmetry. Given a hyperboloid, one can choose a Cartesian coordinate system such that the hyperboloid is defined by one of the following equations: : + - = 1, or : + - = -1. The coordinate axes are axes of symmetry of the hyperboloid and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperboloid Model
In geometry, the hyperboloid model, also known as the Minkowski model after Hermann Minkowski, is a model of ''n''-dimensional hyperbolic geometry in which points are represented by points on the forward sheet ''S''+ of a two-sheeted hyperboloid in (''n''+1)-dimensional Minkowski space or by the displacement vectors from the origin to those points, and ''m''-planes are represented by the intersections of (''m''+1)-planes passing through the origin in Minkowski space with ''S''+ or by wedge products of ''m'' vectors. Hyperbolic space is embedded isometrically in Minkowski space; that is, the hyperbolic distance function is inherited from Minkowski space, analogous to the way spherical distance is inherited from Euclidean distance when the ''n''-sphere is embedded in (''n''+1)-dimensional Euclidean space. Other models of hyperbolic space can be thought of as map projections of ''S''+: the Beltrami–Klein model is the projection of ''S''+ through the origin onto a plane perpend ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
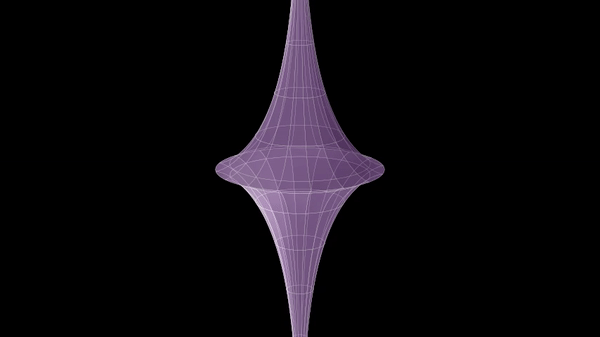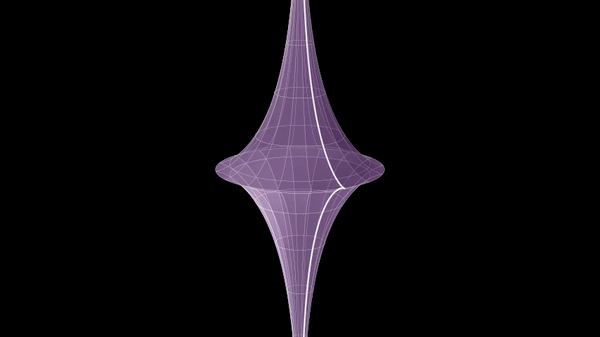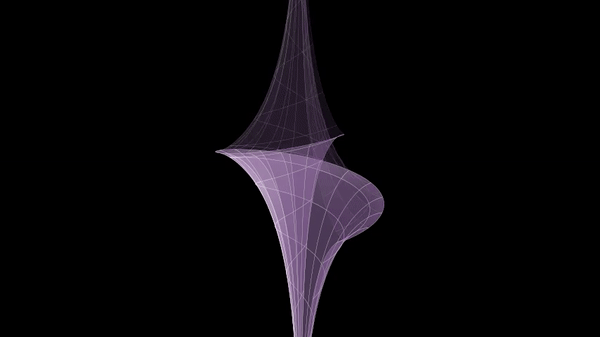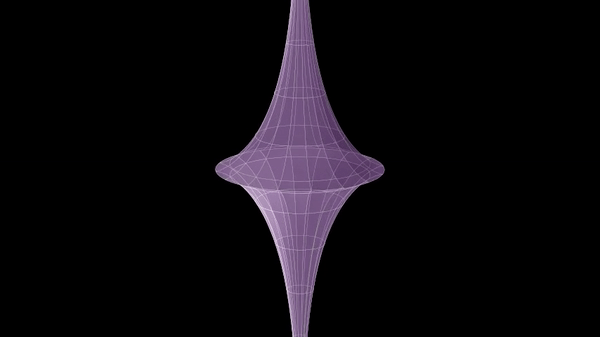
Deforming A Pseudosphere To Dini's Surface
Deformation can refer to: * Deformation (engineering), changes in an object's shape or form due to the application of a force or forces. ** Deformation (physics), such changes considered and analyzed as displacements of continuum bodies. * Deformation (meteorology), a measure of the rate at which the shapes of clouds and other fluid bodies change. * Deformation (mathematics), the study of conditions leading to slightly different solutions of mathematical equations, models and problems. * Deformation (volcanology), a measure of the rate at which the shapes of volcanoes change. * Deformation (biology), a harmful mutation or other deformation in an organism. See also * Deformity (medicine), a major difference in the shape of a body part or organ compared to its common or average shape. * Plasticity (physics) In physics and materials science, plasticity, also known as plastic deformation, is the ability of a solid material to undergo permanent deformation, a non-reversi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Universal Covering Space
A covering of a topological space X is a continuous map \pi : E \rightarrow X with special properties. Definition Let X be a topological space. A covering of X is a continuous map : \pi : E \rightarrow X such that there exists a discrete space D and for every x \in X an open neighborhood U \subset X, such that \pi^(U)= \displaystyle \bigsqcup_ V_d and \pi, _:V_d \rightarrow U is a homeomorphism for every d \in D . Often, the notion of a covering is used for the covering space E as well as for the map \pi : E \rightarrow X. The open sets V_ are called sheets, which are uniquely determined up to a homeomorphism if U is connected. For each x \in X the discrete subset \pi^(x) is called the fiber of x. The degree of a covering is the cardinality of the space D. If E is path-connected, then the covering \pi : E \rightarrow X is denoted as a path-connected covering. Examples * For every topological space X there exists the covering \pi:X \rightarrow X with \pi(x)=x, which is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poincaré Half-plane Model
In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane, denoted below as H = \, together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry. Equivalently the Poincaré half-plane model is sometimes described as a complex plane where the imaginary part (the ''y'' coordinate mentioned above) is positive. The Poincaré half-plane model is named after Henri Poincaré, but it originated with Eugenio Beltrami who used it, along with the Klein model and the Poincaré disk model, to show that hyperbolic geometry was equiconsistent with Euclidean geometry. This model is conformal which means that the angles measured at a point are the same in the model as they are in the actual hyperbolic plane. The Cayley transform provides an isometry between the half-plane model and the Poincaré disk model. This model can be generalized to model an n+1 dimensional hyperbolic space by replacing the real number ''x'' b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Horocycle
In hyperbolic geometry, a horocycle (), sometimes called an oricycle, oricircle, or limit circle, is a curve whose normal or perpendicular geodesics all converge asymptotically in the same direction. It is the two-dimensional case of a horosphere (or ''orisphere''). The centre of a horocycle is the ideal point where all normal geodesics asymptotically converge. Two horocycles who have the same centre are concentric. Although it appears as if two concentric horocycles cannot have the same length or curvature, in fact any two horocycles are congruent. A horocycle can also be described as the limit of the circles that share a tangent in a given point, as their radii go towards infinity. In Euclidean geometry, such a "circle of infinite radius" would be a straight line, but in hyperbolic geometry it is a horocycle (a curve). From the convex side the horocycle is approximated by hypercycles whose distances from their axis go towards infinity. Properties * Through every pair ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covering Space
A covering of a topological space X is a continuous map \pi : E \rightarrow X with special properties. Definition Let X be a topological space. A covering of X is a continuous map : \pi : E \rightarrow X such that there exists a discrete space D and for every x \in X an open neighborhood U \subset X, such that \pi^(U)= \displaystyle \bigsqcup_ V_d and \pi, _:V_d \rightarrow U is a homeomorphism for every d \in D . Often, the notion of a covering is used for the covering space E as well as for the map \pi : E \rightarrow X. The open sets V_ are called sheets, which are uniquely determined up to a homeomorphism if U is connected. For each x \in X the discrete subset \pi^(x) is called the fiber of x. The degree of a covering is the cardinality of the space D. If E is path-connected, then the covering \pi : E \rightarrow X is denoted as a path-connected covering. Examples * For every topological space X there exists the covering \pi:X \rightarrow X with \pi(x)=x, which is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodesics On The Pseudosphere And Three Other Models Of Hyperbolic Geometry
In geometry, a geodesic () is a curve representing in some sense the shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a "straight line". The noun ''geodesic'' and the adjective '' geodetic'' come from ''geodesy'', the science of measuring the size and shape of Earth, though many of the underlying principles can be applied to any ellipsoidal geometry. In the original sense, a geodesic was the shortest route between two points on the Earth's surface. For a spherical Earth, it is a segment of a great circle (see also great-circle distance). The term has since been generalized to more abstract mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph. In a Riemannian manifold or submanifold, geodesics are characterised by the property of having vanishing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume
Volume is a measure of occupied three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). The definition of length (cubed) is interrelated with volume. The volume of a container is generally understood to be the capacity of the container; i.e., the amount of fluid (gas or liquid) that the container could hold, rather than the amount of space the container itself displaces. In ancient times, volume is measured using similar-shaped natural containers and later on, standardized containers. Some simple three-dimensional shapes can have its volume easily calculated using arithmetic formulas. Volumes of more complicated shapes can be calculated with integral calculus if a formula exists for the shape's boundary. Zero-, one- and two-dimensional objects have no volume; in fourth and higher dimensions, an analogous concept to the no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |