
In
topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformat ...
, a covering or covering projection is a
map between
topological space
In mathematics, a topological space is, roughly speaking, a Geometry, geometrical space in which Closeness (mathematics), closeness is defined but cannot necessarily be measured by a numeric Distance (mathematics), distance. More specifically, a to ...
s that, intuitively,
locally acts like a
projection of multiple copies of a space onto itself. In particular, coverings are special types of
local homeomorphisms. If
is a covering,
is said to be a covering space or cover of
, and
is said to be the base of the covering, or simply the base. By
abuse of terminology,
and
may sometimes be called covering spaces as well. Since coverings are local homeomorphisms, a covering space is a special kind of
étalé space.
Covering spaces first arose in the context of
complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic ...
(specifically, the technique of
analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of definition of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a ne ...
), where they were introduced by
Riemann as domains on which naturally
multivalued complex functions become single-valued. These spaces are now called
Riemann surfaces.
Covering spaces are an important tool in several areas of mathematics. In modern
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, covering spaces (or
branched coverings, which have slightly weaker conditions) are used in the construction of
manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a N ...
s,
orbifolds, and the
morphisms between them. In
algebraic topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariant (mathematics), invariants that classification theorem, classify topological spaces up t ...
, covering spaces are closely related to the
fundamental group: for one, since all coverings have the
homotopy lifting property, covering spaces are an important tool in the calculation of
homotopy groups. A standard example in this vein is the calculation of the
fundamental group of the circle by means of the covering of
by
(see
below).
Under certain conditions, covering spaces also exhibit a
Galois correspondence with the subgroups of the fundamental group.
Definition
Let
be a topological space. A covering of
is a continuous map
:
such that for every
there exists an
open neighborhood of
and a
discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points form a , meaning they are '' isolated'' from each other in a certain sense. The discrete topology is the finest to ...
such that
and
is a
homeomorphism
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function ...
for every
.
The open sets
are called sheets, which are uniquely determined up to homeomorphism if
is
connected. For each
the discrete set
is called the fiber of
. If
is connected (and
is non-empty), it can be shown that
is
surjective, and the
cardinality
The thumb is the first digit of the hand, next to the index finger. When a person is standing in the medical anatomical position (where the palm is facing to the front), the thumb is the outermost digit. The Medical Latin English noun for thum ...
of
is the same for all
; this value is called the degree of the covering. If
is
path-connected, then the covering
is called a path-connected covering. This definition is equivalent to the statement that
is a locally trivial
fiber bundle.
Some authors also require that
be surjective in the case that
is not connected.
Examples
* For every topological space
, the
identity map
Graph of the identity function on the real numbers
In mathematics, an identity function, also called an identity relation, identity map or identity transformation, is a function that always returns the value that was used as its argument, unc ...
is a covering. Likewise for any discrete space
the projection
taking
is a covering. Coverings of this type are called trivial coverings; if
has finitely many (say
) elements, the covering is called the trivial ''
-sheeted'' covering of
.
* The map
with
is a covering of the
unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
. The base of the covering is
and the covering space is
. For any point
such that
, the set
is an open neighborhood of
. The preimage of
under
is
*:
: and the sheets of the covering are
for
The fiber of
is
::
* Another covering of the unit circle is the map
with
for some positive
For an open neighborhood
of an
, one has:
::
.
* A map which is a
local homeomorphism but not a covering of the unit circle is
with
. There is a sheet of an open neighborhood of
, which is not mapped homeomorphically onto
.
Properties
Local homeomorphism
Since a covering
maps each of the disjoint open sets of
homeomorphically onto
it is a local homeomorphism, i.e.
is a continuous map and for every
there exists an open neighborhood
of
, such that
is a homeomorphism.
It follows that the covering space
and the base space
locally share the same properties.
* If
is a connected and
non-orientable manifold, then there is a covering
of degree
, whereby
is a connected and orientable manifold.
* If
is a connected
Lie group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable.
A manifold is a space that locally resembles Eucli ...
, then there is a covering
which is also a
Lie group homomorphism and
is a Lie group.
* If
is a
graph, then it follows for a covering
that
is also a graph.
* If
is a connected
manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a N ...
, then there is a covering
, whereby
is a connected and
simply connected
In topology, a topological space is called simply connected (or 1-connected, or 1-simply connected) if it is path-connected and every Path (topology), path between two points can be continuously transformed into any other such path while preserving ...
manifold.
* If
is a connected
Riemann surface, then there is a covering
which is also a holomorphic map and
is a connected and simply connected Riemann surface.
Factorisation
Let
and
be path-connected, locally path-connected spaces, and
and
be continuous maps, such that the diagram
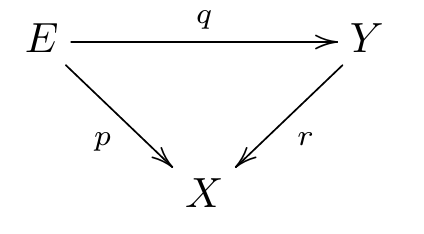
commutes.
* If
and
are coverings, so is
.
* If
and
are coverings, so is
.
Product of coverings
Let
and
be topological spaces and
and
be coverings, then
with
is a covering.
However, coverings of
are not all of this form in general.
Equivalence of coverings
Let
be a topological space and
and
be coverings. Both coverings are called equivalent, if there exists a homeomorphism
, such that the diagram
commutes. If such a homeomorphism exists, then one calls the covering spaces
and
isomorphic
In mathematics, an isomorphism is a structure-preserving mapping or morphism between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between the ...
.
Lifting property
All coverings satisfy the
lifting property, i.e.:
Let
be the
unit interval and
be a covering. Let
be a continuous map and
be a lift of
, i.e. a continuous map such that
. Then there is a uniquely determined, continuous map
for which
and which is a lift of
, i.e.
.
If
is a path-connected space, then for
it follows that the map
is a lift of a
path in
and for
it is a lift of a
homotopy
In topology, two continuous functions from one topological space to another are called homotopic (from and ) if one can be "continuously deformed" into the other, such a deformation being called a homotopy ( ; ) between the two functions. ...
of paths in
.
As a consequence, one can show that the
fundamental group of the unit circle is an
infinite cyclic group, which is generated by the homotopy classes of the loop
with
.
Let
be a path-connected space and
be a connected covering. Let
be any two points, which are connected by a path
, i.e.
and
. Let
be the unique lift of
, then the map
:
with
is
bijective
In mathematics, a bijection, bijective function, or one-to-one correspondence is a function between two sets such that each element of the second set (the codomain) is the image of exactly one element of the first set (the domain). Equival ...
.
If
is a path-connected space and
a connected covering, then the induced
group homomorphism
In mathematics, given two groups, (''G'',∗) and (''H'', ·), a group homomorphism from (''G'',∗) to (''H'', ·) is a function ''h'' : ''G'' → ''H'' such that for all ''u'' and ''v'' in ''G'' it holds that
: h(u*v) = h(u) \cdot h(v)
whe ...
:
with
 In
In  commutes.
* If and are coverings, so is .
* If and are coverings, so is .
commutes.
* If and are coverings, so is .
* If and are coverings, so is .
 commutes.
* If and are coverings, so is .
* If and are coverings, so is .
commutes.
* If and are coverings, so is .
* If and are coverings, so is .