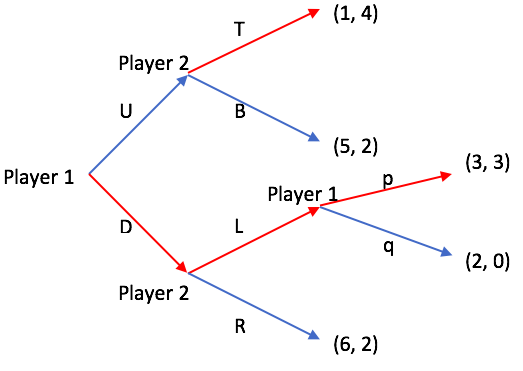
|
Proper Subgame
In game theory, a subgame is any part (a subset) of a game that meets the following criteria (the following terms allude to a game described in extensive form): #It has a single initial node that is the only member of that node's information set (i.e. the initial node is in a singleton information set). #If a node is contained in the subgame then so are all of its successors. #If a node in a particular information set is in the subgame then all members of that information set belong to the subgame. It is a notion used in the solution concept of subgame perfect Nash equilibrium, a refinement of the Nash equilibrium that eliminates non-credible threats. The key feature of a subgame is that it, when seen in isolation, constitutes a game in its own right. When the initial node of a subgame is reached in a larger game, players can concentrate only on that subgame; they can ignore the history of the rest of the game (provided they know what subgame they are playing). This is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions among rational agents. Myerson, Roger B. (1991). ''Game Theory: Analysis of Conflict,'' Harvard University Press, p.&nbs1 Chapter-preview links, ppvii–xi It has applications in all fields of social science, as well as in logic, systems science and computer science. Originally, it addressed two-person zero-sum games, in which each participant's gains or losses are exactly balanced by those of other participants. In the 21st century, game theory applies to a wide range of behavioral relations; it is now an umbrella term for the science of logical decision making in humans, animals, as well as computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum game and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extensive Form Game
An extensive-form game is a specification of a game in game theory, allowing (as the name suggests) for the explicit representation of a number of key aspects, like the sequencing of players' possible moves, their choices at every decision point, the (possibly imperfect) information each player has about the other player's moves when they make a decision, and their payoffs for all possible game outcomes. Extensive-form games also allow for the representation of incomplete information in the form of chance events modeled as " moves by nature". Finite extensive-form games Some authors, particularly in introductory textbooks, initially define the extensive-form game as being just a game tree with payoffs (no imperfect or incomplete information), and add the other elements in subsequent chapters as refinements. Whereas the rest of this article follows this gentle approach with motivating examples, we present upfront the finite extensive-form games as (ultimately) constructed here. This ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Set (game Theory)
In game theory, an information set is a set that, for a particular player, given what that player has observed shows the decision vertices available to the player which are undistinguishable to them at the current point in the game. For a better idea on decision vertices, refer to Figure 1. If the game has perfect information, every information set contains only one member, namely the point actually reached at that stage of the game, since each player knows the exact mix of chance moves and player strategies up to the current point in the game. Otherwise, it is the case that some players cannot be sure exactly what has taken place so far in the game and what their position is. Information sets are used in extensive form games and are often depicted in game trees. Game trees show the path from the start of a game and the subsequent paths that can be made depending on each player's next move. Information sets can be easily depicted in game trees to display each player's possible move ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singleton (mathematics)
In mathematics, a singleton, also known as a unit set or one-point set, is a set with exactly one element. For example, the set \ is a singleton whose single element is 0. Properties Within the framework of Zermelo–Fraenkel set theory, the axiom of regularity guarantees that no set is an element of itself. This implies that a singleton is necessarily distinct from the element it contains, thus 1 and are not the same thing, and the empty set is distinct from the set containing only the empty set. A set such as \ is a singleton as it contains a single element (which itself is a set, however, not a singleton). A set is a singleton if and only if its cardinality is . In von Neumann's set-theoretic construction of the natural numbers, the number 1 is ''defined'' as the singleton \. In axiomatic set theory, the existence of singletons is a consequence of the axiom of pairing: for any set ''A'', the axiom applied to ''A'' and ''A'' asserts the existence of \, which is the same a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solution Concept
In game theory, a solution concept is a formal rule for predicting how a game will be played. These predictions are called "solutions", and describe which strategies will be adopted by players and, therefore, the result of the game. The most commonly used solution concepts are equilibrium concepts, most famously Nash equilibrium. Many solution concepts, for many games, will result in more than one solution. This puts any one of the solutions in doubt, so a game theorist may apply a refinement to narrow down the solutions. Each successive solution concept presented in the following improves on its predecessor by eliminating implausible equilibria in richer games. Formal definition Let \Gamma be the class of all games and, for each game G \in \Gamma, let S_G be the set of strategy profiles of G. A ''solution concept'' is an element of the direct product \Pi_2^; ''i.e''., a function F: \Gamma \rightarrow \bigcup\nolimits_ 2^ such that F(G) \subseteq S_G for all G \in \Gamma. Ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subgame Perfect Equilibrium
In game theory, a subgame perfect equilibrium (or subgame perfect Nash equilibrium) is a refinement of a Nash equilibrium used in dynamic games. A strategy profile is a subgame perfect equilibrium if it represents a Nash equilibrium of every subgame of the original game. Informally, this means that at any point in the game, the players' behavior from that point onward should represent a Nash equilibrium of the continuation game (i.e. of the subgame), no matter what happened before. Every finite extensive game with perfect recall has a subgame perfect equilibrium. Perfect recall is a term introduced by Harold W. Kuhn in 1953 and ''"equivalent to the assertion that each player is allowed by the rules of the game to remember everything he knew at previous moves and all of his choices at those moves"''. A common method for determining subgame perfect equilibria in the case of a finite game is backward induction. Here one first considers the last actions of the game and determ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nash Equilibrium
In game theory, the Nash equilibrium, named after the mathematician John Nash, is the most common way to define the solution of a non-cooperative game involving two or more players. In a Nash equilibrium, each player is assumed to know the equilibrium strategies of the other players, and no one has anything to gain by changing only one's own strategy. The principle of Nash equilibrium dates back to the time of Cournot, who in 1838 applied it to competing firms choosing outputs. If each player has chosen a strategy an action plan based on what has happened so far in the game and no one can increase one's own expected payoff by changing one's strategy while the other players keep their's unchanged, then the current set of strategy choices constitutes a Nash equilibrium. If two players Alice and Bob choose strategies A and B, (A, B) is a Nash equilibrium if Alice has no other strategy available that does better than A at maximizing her payoff in response to Bob choosing B, and Bob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-credible Threat
A non-credible threat is a term used in game theory and economics to describe a threat in a sequential game that a ''rational'' player would not actually carry out, because it would not be in his best interest to do so. A threat, and its counterparta commitment, are both defined by American economist and Nobel prize winner, T.C. Schelling, who stated that: "A announces that B's behaviour will lead to a response from A. If this response is a reward, then the announcement is a commitment; if this response is a penalty, then the announcement is a threat." While a player might make a threat, it is only deemed credible if it serves the best interest of the player.Heifetz, A., & Yalon-Fortus, J. (2012). Game Theory: Interactive Strategies in Economics and Management. Cambridge University Press. ProQuest Ebook Central In other words, the player would be willing to carry through with the action that is being threatened regardless of the choice of the other player. This is based on the ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Game
In game theory, a Bayesian game is a game that models the outcome of player interactions using aspects of Bayesian probability. Bayesian games are notable because they allowed, for the first time in game theory, for the specification of the solutions to games with incomplete information. Hungarian economist John C. Harsanyi introduced the concept of Bayesian games in three papers from 1967 and 1968: He was awarded the Nobel Prize for these and other contributions to game theory in 1994. Roughly speaking, Harsanyi defined Bayesian games in the following way: players are assigned by nature at the start of the game a set of characteristics. By mapping probability distributions to these characteristics and by calculating the outcome of the game using Bayesian probability, the result is a game whose solution is, for technical reasons, far easier to calculate than a similar game in a non-Bayesian context. For those technical reasons, see the Specification of games section in this article ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Game
In game theory, a Bayesian game is a game that models the outcome of player interactions using aspects of Bayesian probability. Bayesian games are notable because they allowed, for the first time in game theory, for the specification of the solutions to games with incomplete information. Hungarian economist John C. Harsanyi introduced the concept of Bayesian games in three papers from 1967 and 1968: He was awarded the Nobel Prize for these and other contributions to game theory in 1994. Roughly speaking, Harsanyi defined Bayesian games in the following way: players are assigned by nature at the start of the game a set of characteristics. By mapping probability distributions to these characteristics and by calculating the outcome of the game using Bayesian probability, the result is a game whose solution is, for technical reasons, far easier to calculate than a similar game in a non-Bayesian context. For those technical reasons, see the Specification of games section in this article ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions among rational agents. Myerson, Roger B. (1991). ''Game Theory: Analysis of Conflict,'' Harvard University Press, p.&nbs1 Chapter-preview links, ppvii–xi It has applications in all fields of social science, as well as in logic, systems science and computer science. Originally, it addressed two-person zero-sum games, in which each participant's gains or losses are exactly balanced by those of other participants. In the 21st century, game theory applies to a wide range of behavioral relations; it is now an umbrella term for the science of logical decision making in humans, animals, as well as computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum game and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
