|
Principal Axis (mechanics)
The moment of inertia, otherwise known as the mass moment of inertia, angular mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis, akin to how mass determines the force needed for a desired acceleration. It depends on the body's mass distribution and the axis chosen, with larger moments requiring more torque to change the body's rate of rotation. It is an extensive (additive) property: for a point mass the moment of inertia is simply the mass times the square of the perpendicular distance to the axis of rotation. The moment of inertia of a rigid composite system is the sum of the moments of inertia of its component subsystems (all taken about the same axis). Its simplest definition is the second moment of mass with respect to distance from an axis. For bodies constrained to rotate in a plane, only their moment of inertia about an axis p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flywheel
A flywheel is a mechanical device which uses the conservation of angular momentum to store rotational energy; a form of kinetic energy proportional to the product of its moment of inertia and the square of its rotational speed. In particular, assuming the flywheel's moment of inertia is constant (i.e., a flywheel with fixed mass and second moment of area revolving about some fixed axis) then the stored (rotational) energy is directly associated with the square of its rotational speed. Since a flywheel serves to store mechanical energy for later use, it is natural to consider it as a kinetic energy analogue of an electrical inductor. Once suitably abstracted, this shared principle of energy storage is described in the generalized concept of an accumulator. As with other types of accumulators, a flywheel inherently smooths sufficiently small deviations in the power output of a system, thereby effectively playing the role of a low-pass filter with respect to the mechanical velocity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed system remains constant. Angular momentum has both a direction and a magnitude, and both are conserved. Bicycles and motorcycles, frisbees, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it. The three-dimensional angular momentum for a point particle is classically represented as a pseudovector , the cross product of the particle's position vector (relative to some origin) and its momentum vector; the latter is in Newtonian mechanics. Unlike linear momentum, angular m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Figure Skating Spins
Spins are an element in figure skating in which the skater rotates, centered on a single point on the ice, while holding one or more body positions. They are performed by all disciplines of the sport, single skating, pair skating, and ice dance, and are a required element in most figure skating competitions. As ''The New York Times'' says, "While jumps look like sport, spins look more like art. While jumps provide the suspense, spins provide the scenery, but there is so much more to the scenery than most viewers have time or means to grasp". According to world champion and figure skating commentator Scott Hamilton, spins are often used "as breathing points or transitions to bigger things" Figure skating spins, along with jumps, spirals, and spread eagles were originally individual compulsory figures, sometimes special figures. Unlike jumps, spins were a "graceful and appreciated"Hines, p. 103 part of figure skating throughout the 19th century. They advanced between World War I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cup Of Russia 2010 - Yuko Kawaguti (2)
A cup is an open-top used to hold hot or cold liquids for pouring or drinking; while mainly used for drinking, it also can be used to store solids for pouring (e.g., sugar, flour, grains, salt). Cups may be made of glass, metal, china, clay, wood, stone, polystyrene, plastic, aluminium or other materials, and are usually fixed with a stem, handles, or other adornments. Cups are used for quenching thirst across a wide range of cultures and social classes, and different styles of cups may be used for different liquids or in different situations. Cups of different styles may be used for different types of liquids or other foodstuffs (e.g. teacups and measuring cups), in different situations (e.g. at water stations or in ceremonies and rituals), or for decoration. Rigby 2003: p. 573–574. History Cups are an improvement on using cupped hands or feet to hold liquids. They have almost certainly been used since before recorded history, and have been found at archaeological sites th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Centroid
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any object in ''n''-dimensional Euclidean space. In geometry, one often assumes uniform mass density, in which case the ''barycenter'' or ''center of mass'' coincides with the centroid. Informally, it can be understood as the point at which a cutout of the shape (with uniformly distributed mass) could be perfectly balanced on the tip of a pin. In physics, if variations in gravity are considered, then a ''center of gravity'' can be defined as the weighted mean of all points weighted by their specific weight. In geography, the centroid of a radial projection of a region of the Earth's surface to sea level is the region's geographical center. History The term "centroid" is of recent coinage (1814). It is used as a substitute for the older te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flywheel
A flywheel is a mechanical device which uses the conservation of angular momentum to store rotational energy; a form of kinetic energy proportional to the product of its moment of inertia and the square of its rotational speed. In particular, assuming the flywheel's moment of inertia is constant (i.e., a flywheel with fixed mass and second moment of area revolving about some fixed axis) then the stored (rotational) energy is directly associated with the square of its rotational speed. Since a flywheel serves to store mechanical energy for later use, it is natural to consider it as a kinetic energy analogue of an electrical inductor. Once suitably abstracted, this shared principle of energy storage is described in the generalized concept of an accumulator. As with other types of accumulators, a flywheel inherently smooths sufficiently small deviations in the power output of a system, thereby effectively playing the role of a low-pass filter with respect to the mechanical velocity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
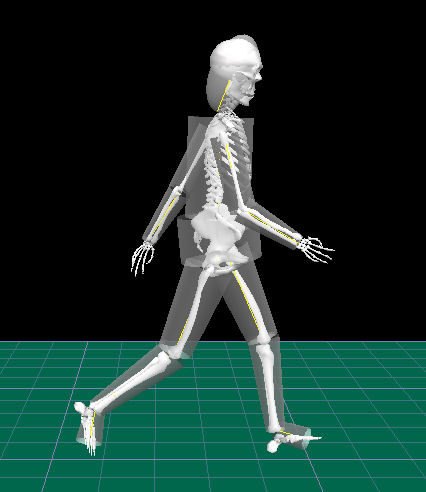
Rigid Body Dynamics
In the physical science of dynamics, rigid-body dynamics studies the movement of systems of interconnected bodies under the action of external forces. The assumption that the bodies are ''rigid'' (i.e. they do not deform under the action of applied forces) simplifies analysis, by reducing the parameters that describe the configuration of the system to the translation and rotation of reference frames attached to each body. This excludes bodies that display fluid, highly elastic, and plastic behavior. The dynamics of a rigid body system is described by the laws of kinematics and by the application of Newton's second law (kinetics) or their derivative form, Lagrangian mechanics. The solution of these equations of motion provides a description of the position, the motion and the acceleration of the individual components of the system, and overall the system itself, as a function of time. The formulation and solution of rigid body dynamics is an important tool in the computer si ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinetic Energy
In physics, the kinetic energy of an object is the energy that it possesses due to its motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes. The same amount of work is done by the body when decelerating from its current speed to a state of rest. Formally, a kinetic energy is any term in a system's Lagrangian which includes a derivative with respect to time. In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2. In relativistic mechanics, this is a good approximation only when ''v'' is much less than the speed of light. The standard unit of kinetic energy is the joule, while the English unit of kinetic energy is the foot-pound. History and etymology The adjective ''kinetic'' has its roots in the Greek word κίνησις ''kinesis'', m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler's Laws
In classical mechanics, Euler's laws of motion are equations of motion which extend Newton's laws of motion for point particle to rigid body motion. They were formulated by Leonhard Euler about 50 years after Isaac Newton formulated his laws. Overview Euler's first law Euler's first law states that the rate of change of linear momentum of a rigid body is equal to the resultant of all the external forces acting on the body: : F_\text = \frac. Internal forces between the particles that make up a body do not contribute to changing the momentum of the body as there is an equal and opposite force resulting in no net effect. The linear momentum of a rigid body is the product of the mass of the body and the velocity of its center of mass . Euler's second law Euler's second law states that the rate of change of angular momentum about a point that is fixed in an inertial reference frame (often the center of mass of the body), is equal to the sum of the external moments of force ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leonhard Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in many other branches of mathematics such as analytic number theory, complex analysis, and infinitesimal calculus. He introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is also known for his work in mechanics, fluid dynamics, optics, astronomy and music theory. Euler is held to be one of the greatest mathematicians in history and the greatest of the 18th century. A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is the master of us all." Carl Friedrich Gauss remarked: "The study of Euler's works will remain the best school for the different fields of mathematics, and nothing else can replace it." Euler is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging back and forth. The time for one complete cycle, a left swing and a right swing, is called the period. The period depends on the length of the pendulum and also to a slight degree on the amplitude, the width of the pendulum's swing. From the first scientific investigations of the pendulum around 1602 by Galileo Galilei, the regular motion of pendulums was used for timekeeping and was the world's most accurate timekeeping technology until the 1930s. The pendulum clock invented by Christiaan Huygens in 1658 became the world's standard timekeeper, used in homes and offices for 270 years, and ac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Christiaan Huygens
Christiaan Huygens, Lord of Zeelhem, ( , , ; also spelled Huyghens; la, Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor, who is regarded as one of the greatest scientists of all time and a major figure in the Scientific Revolution. In physics, Huygens made groundbreaking contributions in optics and mechanics, while as an astronomer he is chiefly known for his studies of the rings of Saturn and the discovery of its moon Titan. As an engineer and inventor, he improved the design of telescopes and invented the pendulum clock, a breakthrough in timekeeping and the most accurate timekeeper for almost 300 years. An exceptionally talented mathematician and physicist, Huygens was the first to idealize a physical problem by a set of mathematical parameters, and the first to fully mathematize a mechanistic explanation of an unobservable physical phenomenon.Dijksterhuis, F.J. (2008) Stevin, Huygens and the Dutch republ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Flywheel")
_(20).jpg "Click for more on -> Figure Skating Spins")
.jpg "Click for more on -> Cup Of Russia 2010 - Yuko Kawaguti (2)")
