|
Poincaré–Lindstedt Method
In perturbation theory, the Poincaré–Lindstedt method or Lindstedt–Poincaré method is a technique for uniformly approximating periodic solutions to ordinary differential equations, when regular perturbation approaches fail. The method removes secular terms—terms growing without bound—arising in the straightforward application of perturbation theory to weakly nonlinear problems with finite oscillatory solutions. The method is named after Henri Poincaré, and Anders Lindstedt. Example: the Duffing equation The undamped, unforced Duffing equation is given by :\ddot + x + \varepsilon\, x^3 = 0\, for ''t'' > 0, with 0 < ''ε'' ≪ 1.J. David Logan. ''Applied Mathematics'', Second Edition, John Wiley & Sons, 1997. . Consider initial conditions : A perturbation-series ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perturbation Theory
In mathematics and applied mathematics, perturbation theory comprises methods for finding an approximate solution to a problem, by starting from the exact solution of a related, simpler problem. A critical feature of the technique is a middle step that breaks the problem into "solvable" and "perturbative" parts. In perturbation theory, the solution is expressed as a power series in a small parameter The first term is the known solution to the solvable problem. Successive terms in the series at higher powers of \varepsilon usually become smaller. An approximate 'perturbation solution' is obtained by truncating the series, usually by keeping only the first two terms, the solution to the known problem and the 'first order' perturbation correction. Perturbation theory is used in a wide range of fields, and reaches its most sophisticated and advanced forms in quantum field theory. Perturbation theory (quantum mechanics) describes the use of this method in quantum mechanics. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to describe oscillations, waves, and other phenomena that exhibit periodicity. Any function that is not periodic is called aperiodic. Definition A function is said to be periodic if, for some nonzero constant , it is the case that :f(x+P) = f(x) for all values of in the domain. A nonzero constant for which this is the case is called a period of the function. If there exists a least positive constant with this property, it is called the fundamental period (also primitive period, basic period, or prime period.) Often, "the" period of a function is used to mean its fundamental period. A function with period will repeat on intervals of length , and these intervals are sometimes also referred to as periods of the function. Geometrically, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Differential Equation
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast with the term partial differential equation which may be with respect to ''more than'' one independent variable. Differential equations A linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y +a_1(x)y' + a_2(x)y'' +\cdots +a_n(x)y^+b(x)=0, where , ..., and are arbitrary differentiable functions that do not need to be linear, and are the successive derivatives of the unknown function of the variable . Among ordinary differential equations, linear differential equations play a prominent role for several reasons. Most elementary and special functions that are encountered in physics and applied mathematics are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Secular Variation
The secular variation of a time series is its long-term, non-periodic variation (see decomposition of time series). Whether a variation is perceived as secular or not depends on the available timescale: a variation that is secular over a timescale of centuries may be a segment of what is, over a timescale of millions of years, a periodic variation. Natural quantities often have both periodic and secular variations. Secular variation is sometimes called secular trend or secular drift when the emphasis is on a linear long-term trend. The term is used wherever time series are applicable in history, economics, operations research, biological anthropology, and astronomy (particularly celestial mechanics) such as VSOP (planets). Etymology The word ''secular'', from the Latin root ''saecularis'' ("of an age, occurring once in an age"), has two basic meanings: I. Of or pertaining to the world (from which secularity is derived), and II. Of or belonging to an age or long period. The latte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists because most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems. Typically, the behavior of a nonlinear system is described in mathematics by a nonlinear system of equations, which is a set of simultaneous equations in which the unknowns (or the unknown functions in the case of differential equations) appear as variables of a polynomial of degree higher than one or in the argument of a function which is not a polynomial of degree one. In other words, in a nonlinear system of equations, the equation(s) to be solved cannot be written as a linear combination of the un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Henri Poincaré
Jules Henri Poincaré ( S: stress final syllable ; 29 April 1854 – 17 July 1912) was a French mathematician, theoretical physicist, engineer, and philosopher of science. He is often described as a polymath, and in mathematics as "The Last Universalist", since he excelled in all fields of the discipline as it existed during his lifetime. As a mathematician and physicist, he made many original fundamental contributions to pure and applied mathematics, mathematical physics, and celestial mechanics. In his research on the three-body problem, Poincaré became the first person to discover a chaotic deterministic system which laid the foundations of modern chaos theory. He is also considered to be one of the founders of the field of topology. Poincaré made clear the importance of paying attention to the invariance of laws of physics under different transformations, and was the first to present the Lorentz transformations in their modern symmetrical form. Poincaré discove ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anders Lindstedt
Anders Lindstedt (27 June 1854 – 16 May 1939) was a Swedish mathematician, astronomer, and actuarial scientist, known for the Lindstedt-Poincaré method. Life and work Lindstedt was born in a small village in the district of Sundborns, Dalecarlia a province in central Sweden.Hvar 8 dag, 10:de Årg, No 11, 13 december 1908, sid. 162'.Memoir Anders Lindstedt 27 June 1854-16 May 1939, Journal of the Institute of Actuaries, 70 (1939) p. 269/ref> He obtained a PhD from the University of Lund aged 32 and was subsequently appointed as a lecturer in astronomy. He later went on to a position at the University of Dorpat (then belonging to Russia, now University of Tartu in Estonia) where he worked for around seven years on theoretical astronomy. He combined practical astronomy with an interest in theory, developing especially an interest in the three-body problem This work was to influence Poincaré whose work on the three-body problem led to the discovery that there can be or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
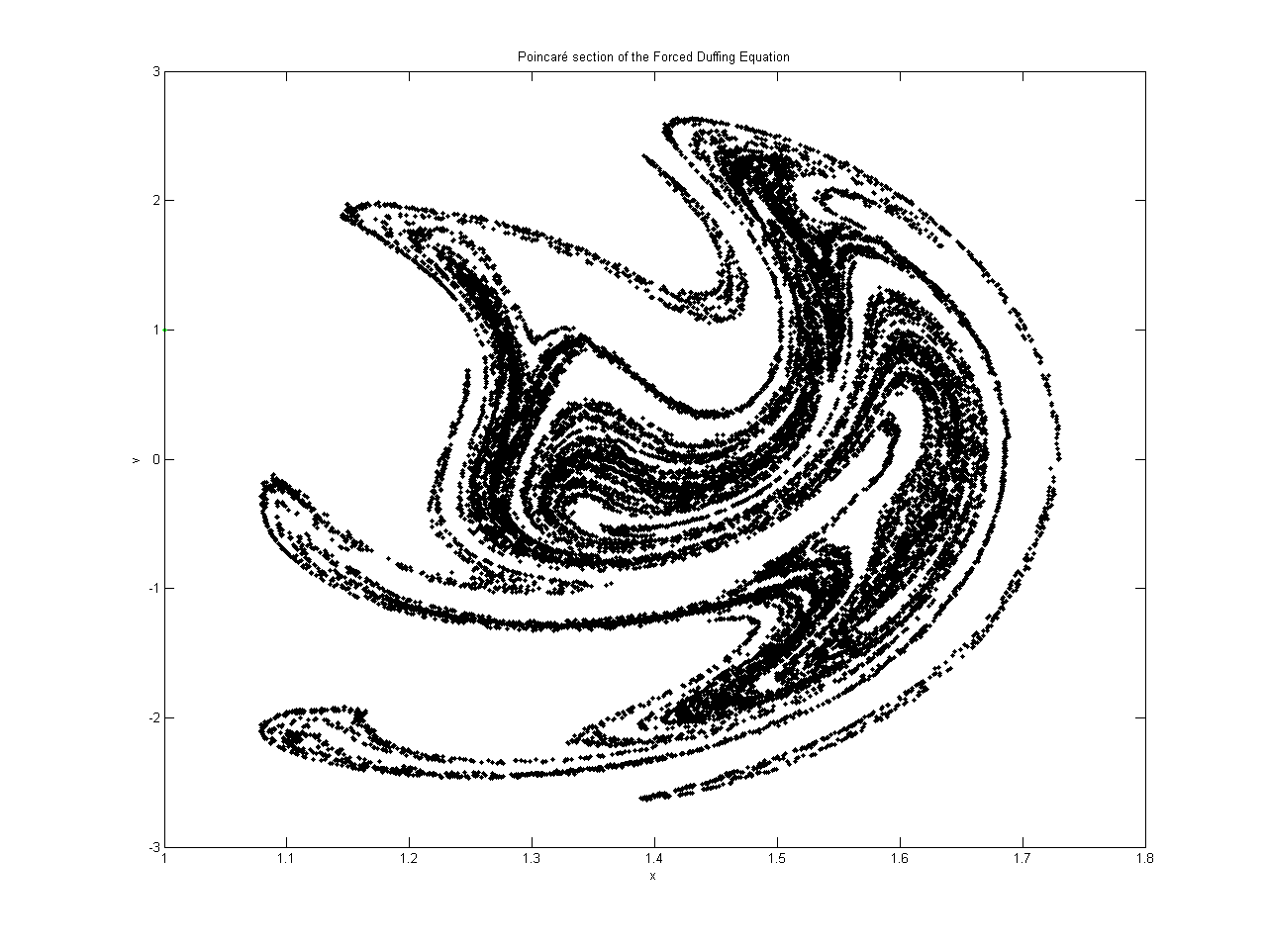
Duffing Equation
The Duffing equation (or Duffing oscillator), named after Georg Duffing (1861–1944), is a non-linear second-order differential equation used to model certain damped and driven oscillators. The equation is given by :\ddot + \delta \dot + \alpha x + \beta x^3 = \gamma \cos (\omega t), where the (unknown) function x=x(t) is the displacement at time t, \dot is the first derivative of x with respect to time, i.e. velocity, and \ddot is the second time-derivative of x, i.e. acceleration. The numbers \delta, \alpha, \beta, \gamma and \omega are given constants. The equation describes the motion of a damped oscillator with a more complex potential than in simple harmonic motion (which corresponds to the case \beta=\delta=0); in physical terms, it models, for example, an elastic pendulum whose spring's stiffness does not exactly obey Hooke's law. The Duffing equation is an example of a dynamical system that exhibits chaotic behavior. Moreover, the Duffing system presents in the f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Secular Term
Secularity, also the secular or secularness (from Latin ''saeculum'', "worldly" or "of a generation"), is the state of being unrelated or neutral in regards to religion. Anything that does not have an explicit reference to religion, either negatively or positively, may be considered secular. Linguistically, a process by which anything becomes secular is named ''secularization'', though the term is mainly reserved for the secularization, secularization of society; and any concept or ideology promoting the secular may be termed ''secularism'', a term generally applied to the ideology dictating secularism, no religious influence on the public sphere. Definitions Historically, the word ''secular'' was not related or linked to religion, but was a freestanding term in Latin which would relate to any mundane endeavour. However, the term, In saecula saeculorum, saecula saeculorumsaeculōrumbeing the genitive plural of saeculum) as found in the New Testament in the Vulgate translation (cir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asymptotic Series
In mathematics, an asymptotic expansion, asymptotic series or Poincaré expansion (after Henri Poincaré) is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular, often infinite, point. Investigations by revealed that the divergent part of an asymptotic expansion is latently meaningful, i.e. contains information about the exact value of the expanded function. The most common type of asymptotic expansion is a power series in either positive or negative powers. Methods of generating such expansions include the Euler–Maclaurin summation formula and integral transforms such as the Laplace and Mellin transforms. Repeated integration by parts will often lead to an asymptotic expansion. Since a '' convergent'' Taylor series fits the definition of asymptotic expansion as well, the phrase "asymptotic series" usually implies a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leading-order
The leading-order terms (or corrections) within a mathematical equation, expression or model are the terms with the largest order of magnitude.J.K.Hunter, ''Asymptotic Analysis and Singular Perturbation Theory'', 2004. http://www.math.ucdavis.edu/~hunter/notes/asy.pdf The sizes of the different terms in the equation(s) will change as the variables change, and hence, which terms are leading-order may also change. A common and powerful way of simplifying and understanding a wide variety of complicated mathematical models is to investigate which terms are the largest (and therefore most important), for particular sizes of the variables and parameters, and analyse the behaviour produced by just these terms (regarding the other smaller terms as negligible). This gives the main behaviour – the true behaviour is only small deviations away from this. This main behaviour may be captured sufficiently well by just the strictly leading-order terms, or it may be decided that slightly smaller ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Frequency
In physics, angular frequency "''ω''" (also referred to by the terms angular speed, circular frequency, orbital frequency, radian frequency, and pulsatance) is a scalar measure of rotation rate. It refers to the angular displacement per unit time (for example, in rotation) or the rate of change of the phase of a sinusoidal waveform (for example, in oscillations and waves), or as the rate of change of the argument of the sine function. Angular frequency (or angular speed) is the magnitude of the pseudovector quantity angular velocity.(UP1) One turn is equal to 2''π'' radians, hence \omega = \frac = , where: *''ω'' is the angular frequency (unit: radians per second), *''T'' is the period (unit: seconds), *''f'' is the ordinary frequency (unit: hertz) (sometimes ''ν''). Units In SI units, angular frequency is normally presented in radians per second, even when it does not express a rotational value. The unit hertz (Hz) is dimensionally equivalent, but by convention it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |