|
Plücker Formula
In mathematics, a Plücker formula, named after Julius Plücker, is one of a family of formulae, of a type first developed by Plücker in the 1830s, that relate certain numeric invariants of algebraic curves to corresponding invariants of their dual curves. The invariant called the genus, common to both the curve and its dual, is connected to the other invariants by similar formulae. These formulae, and the fact that each of the invariants must be a positive integer, place quite strict limitations on their possible values. Plücker invariants and basic equations A curve in this context is defined by a non-degenerate algebraic equation in the complex projective plane. Lines in this plane correspond to points in the dual projective plane and the lines tangent to a given algebraic curve ''C'' correspond to points in an algebraic curve ''C''* called the dual curve. In the correspondence between the projective plane and its dual, points on ''C'' correspond to lines tangent ''C''*, so t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double Points
In geometry, a singular point on a curve is one where the curve is not given by a smooth embedding of a parameter. The precise definition of a singular point depends on the type of curve being studied. Algebraic curves in the plane Algebraic curves in the plane may be defined as the set of points satisfying an equation of the form f(x,y) = 0, where is a polynomial function If is expanded as f = a_0 + b_0 x + b_1 y + c_0 x^2 + 2c_1 xy + c_2 y^2 + \cdots If the origin is on the curve then . If then the implicit function theorem guarantees there is a smooth function so that the curve has the form near the origin. Similarly, if then there is a smooth function so that the curve has the form near the origin. In either case, there is a smooth map from to the plane which defines the curve in the neighborhood of the origin. Note that at the origin b_0 = \frac, \; b_1 = \frac, so the curve is non-singular or ''regular'' at the origin if at least one of the partial derivatives o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quartic Plane Curve
In algebraic geometry, a quartic plane curve is a plane algebraic curve of the fourth degree. It can be defined by a bivariate quartic equation: :Ax^4+By^4+Cx^3y+Dx^2y^2+Exy^3+Fx^3+Gy^3+Hx^2y+Ixy^2+Jx^2+Ky^2+Lxy+Mx+Ny+P=0, with at least one of not equal to zero. This equation has 15 constants. However, it can be multiplied by any non-zero constant without changing the curve; thus by the choice of an appropriate constant of multiplication, any one of the coefficients can be set to 1, leaving only 14 constants. Therefore, the space of quartic curves can be identified with the real projective space It also follows, from Cramer's theorem on algebraic curves, that there is exactly one quartic curve that passes through a set of 14 distinct points in general position, since a quartic has 14 degrees of freedom. A quartic curve can have a maximum of: * Four connected components * Twenty-eight bi-tangents * Three ordinary double points. One may also consider quartic curves over othe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Genus
In algebraic geometry, the geometric genus is a basic birational invariant of algebraic varieties and complex manifolds. Definition The geometric genus can be defined for non-singular complex projective varieties and more generally for complex manifolds as the Hodge number (equal to by Serre duality), that is, the dimension of the canonical linear system plus one. In other words for a variety of complex dimension it is the number of linearly independent holomorphic -forms to be found on .Danilov & Shokurov (1998), p. 53/ref> This definition, as the dimension of : then carries over to any base field, when is taken to be the sheaf of Kähler differentials and the power is the (top) exterior power, the canonical line bundle. The geometric genus is the first invariant of a sequence of invariants called the plurigenera. Case of curves In the case of complex varieties, (the complex loci of) non-singular curves are Riemann surfaces. The algebraic definition of genus ag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inflection Point
In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (British English: inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case of the graph of a function, it is a point where the function changes from being concave (concave downward) to convex (concave upward), or vice versa. For the graph of a function of differentiability class (''f'', its first derivative ''f, and its second derivative ''f'''', exist and are continuous), the condition ''f'' = 0'' can also be used to find an inflection point since a point of ''f'' = 0'' must be passed to change ''f'''' from a positive value (concave upward) to a negative value (concave downward) or vice versa as ''f'''' is continuous; an inflection point of the curve is where ''f'' = 0'' and changes its sign at the point (from positive to negative or from negative to positive). A point where the second derivative vanishes bu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bitangent
In geometry, a bitangent to a curve is a line that touches in two distinct points and and that has the same direction as at these points. That is, is a tangent line at and at . Bitangents of algebraic curves In general, an algebraic curve will have infinitely many secant lines, but only finitely many bitangents. Bézout's theorem implies that an algebraic plane curve with a bitangent must have degree at least 4. The case of the 28 bitangents of a quartic was a celebrated piece of geometry of the nineteenth century, a relationship being shown to the 27 lines on the cubic surface. Bitangents of polygons The four bitangents of two disjoint convex polygons may be found efficiently by an algorithm based on binary search in which one maintains a binary search pointer into the lists of edges of each polygon and moves one of the pointers left or right at each steps depending on where the tangent lines to the edges at the two pointers cross each other. This bitangent calculation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cusp (singularity)
In mathematics, a cusp, sometimes called spinode in old texts, is a point on a curve where a moving point must reverse direction. A typical example is given in the figure. A cusp is thus a type of singular point of a curve. For a plane curve defined by an analytic, parametric equation :\begin x &= f(t)\\ y &= g(t), \end a cusp is a point where both derivatives of and are zero, and the directional derivative, in the direction of the tangent, changes sign (the direction of the tangent is the direction of the slope \lim (g'(t)/f'(t))). Cusps are ''local singularities'' in the sense that they involve only one value of the parameter , in contrast to self-intersection points that involve more than one value. In some contexts, the condition on the directional derivative may be omitted, although, in this case, the singularity may look like a regular point. For a curve defined by an implicit equation :F(x,y) = 0, which is smooth, cusps are points where the terms of lowest de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acnode
An acnode is an isolated point in the solution set of a polynomial equation in two real variables. Equivalent terms are " isolated point or hermit point". For example the equation :f(x,y)=y^2+x^2-x^3=0 has an acnode at the origin, because it is equivalent to :y^2 = x^2 (x-1) and x^2(x-1) is non-negative only when x ≥ 1 or x = 0. Thus, over the ''real'' numbers the equation has no solutions for x < 1 except for (0, 0). In contrast, over the complex numbers the origin is not isolated since square roots of negative real numbers exist. In fact, the complex solution set of a polynomial equation in two complex variables can never have an isolated point. An acnode is a critical point, or singularity, of the defining polynomial function, in the sense that both partial derivatives and vanish. Further ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crunode
In mathematics, a crunode (archaic) or node is a point where a curve intersects itself so that both branches of the curve have distinct tangent lines at the point of intersection. A crunode is also known as an ''ordinary double point''. For a plane curve, defined as the locus of points , where is a smooth function of variables and ranging over the real numbers, a crunode of the curve is a singularity of the function , where both partial derivatives \tfrac and \tfrac vanish. Further the Hessian matrix of second derivatives will have both positive and negative eigenvalues. See also *Singular point of a curve *Acnode *Cusp *Tacnode In classical algebraic geometry, a tacnode (also called a point of osculation or double cusp). is a kind of singular point of a curve. It is defined as a point where two (or more) osculating circles to the curve at that point are tangent I ... * Saddle point References Curves Algebraic curves {{differential-geometry-stub es: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singular Point Of An Algebraic Variety
In the mathematical field of algebraic geometry, a singular point of an algebraic variety is a point that is 'special' (so, singular), in the geometric sense that at this point the tangent space at the variety may not be regularly defined. In case of varieties defined over the reals, this notion generalizes the notion of local non-flatness. A point of an algebraic variety which is not singular is said to be regular. An algebraic variety which has no singular point is said to be non-singular or smooth. Definition A plane curve defined by an implicit equation :F(x,y)=0, where is a smooth function is said to be ''singular'' at a point if the Taylor series of has order at least at this point. The reason for this is that, in differential calculus, the tangent at the point of such a curve is defined by the equation :(x-x_0)F'_x(x_0,y_0) + (y-y_0)F'_y(x_0,y_0)=0, whose left-hand side is the term of degree one of the Taylor expansion. Thus, if this term is zero, the tangent may n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Julius Plücker
Julius Plücker (16 June 1801 – 22 May 1868) was a German mathematician and physicist. He made fundamental contributions to the field of analytical geometry and was a pioneer in the investigations of cathode rays that led eventually to the discovery of the electron. He also vastly extended the study of Lamé curves. Biography Early years Plücker was born at Elberfeld (now part of Wuppertal). After being educated at Düsseldorf and at the universities of Bonn, Heidelberg and Berlin he went to Paris in 1823, where he came under the influence of the great school of French geometers, whose founder, Gaspard Monge, had only recently died. In 1825 he returned to Bonn, and in 1828 was made professor of mathematics. In the same year he published the first volume of his ''Analytisch-geometrische Entwicklungen'', which introduced the method of "abridged notation". In 1831 he published the second volume, in which he clearly established on a firm and independent basis projectiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
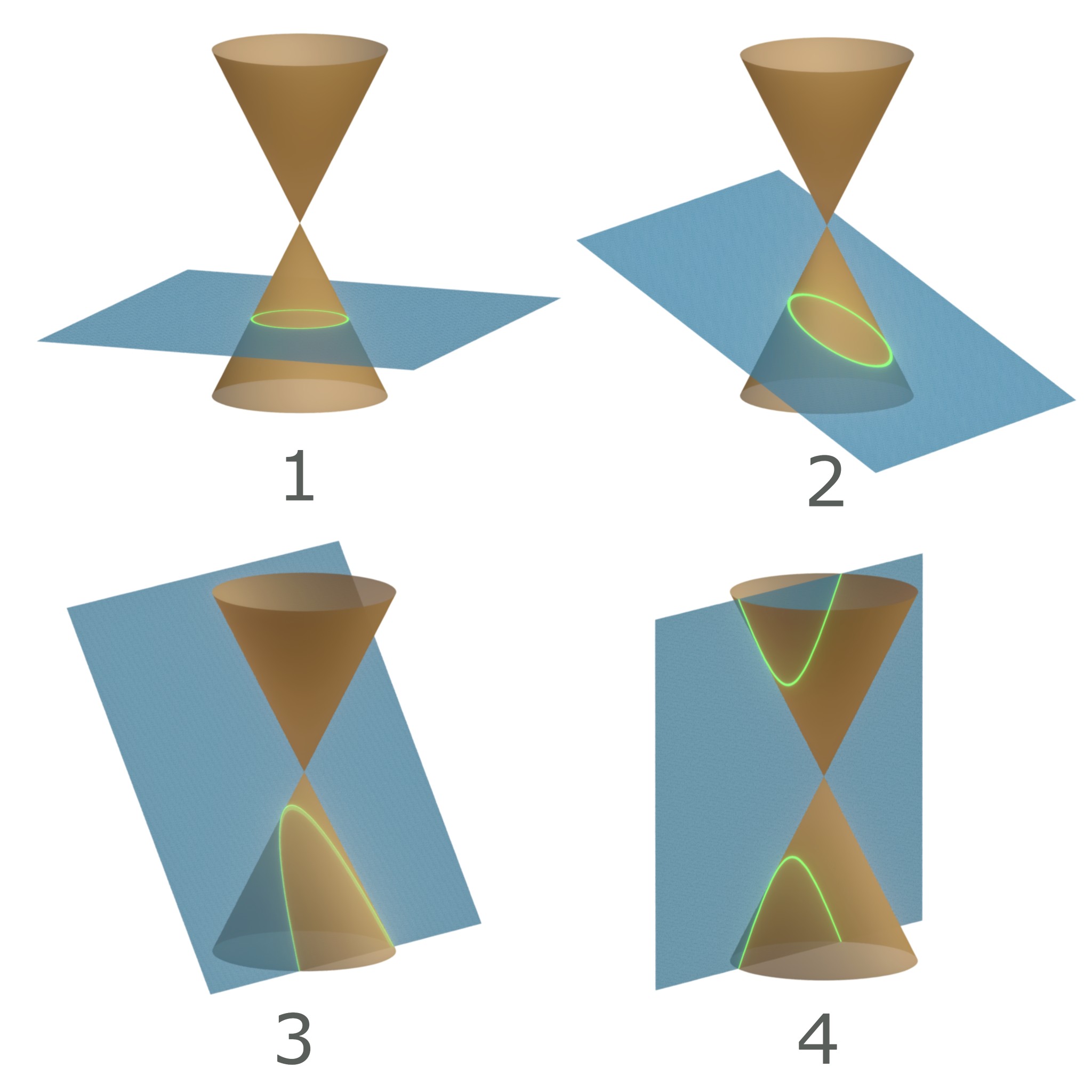
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a ''focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
