|
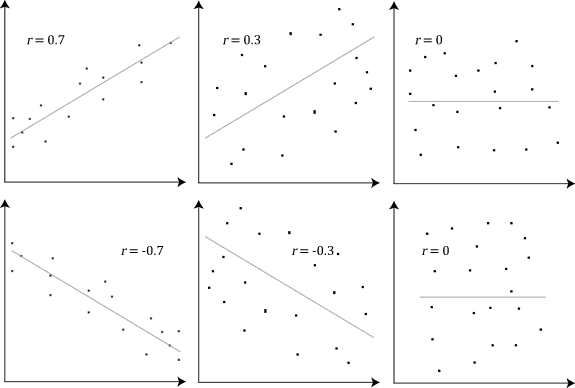
Pearson Product-moment Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC) is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of children from a school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844. The naming ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation Examples2
In statistics, correlation or dependence is any statistical relationship, whether causality, causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are ''line (geometry), linearly'' related. Familiar examples of dependent phenomena include the correlation between the human height, height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causality, causal relationship, because extreme weather causes people to use more ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Score
In statistics, the standard score or ''z''-score is the number of standard deviations by which the value of a raw score (i.e., an observed value or data point) is above or below the mean value of what is being observed or measured. Raw scores above the mean have positive standard scores, while those below the mean have negative standard scores. It is calculated by subtracting the population mean from an individual raw score and then dividing the difference by the Statistical population, population standard deviation. This process of converting a raw score into a standard score is called standardizing or normalizing (however, "normalizing" can refer to many types of ratios; see ''Normalization (statistics), Normalization'' for more). Standard scores are most commonly called ''z''-scores; the two terms may be used interchangeably, as they are in this article. Other equivalent terms in use include z-value, z-statistic, normal score, standardized variable and pull in high energy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invariant Estimator
In statistics, the concept of being an invariant estimator is a criterion that can be used to compare the properties of different estimators for the same quantity. It is a way of formalising the idea that an estimator should have certain intuitively appealing qualities. Strictly speaking, "invariant" would mean that the estimates themselves are unchanged when both the measurements and the parameters are transformed in a compatible way, but the meaning has been extended to allow the estimates to change in appropriate ways with such transformations. The term equivariant estimator is used in formal mathematical contexts that include a precise description of the relation of the way the estimator changes in response to changes to the dataset and parameterisation: this corresponds to the use of " equivariance" in more general mathematics. General setting Background In statistical inference, there are several approaches to estimation theory that can be used to decide immediately what es ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Support (measure Theory)
In mathematics, the support (sometimes topological support or spectrum) of a measure \mu on a measurable topological space (X, \operatorname(X)) is a precise notion of where in the space X the measure "lives". It is defined to be the largest ( closed) subset of X for which every open neighbourhood of every point of the set has positive measure. Motivation A (non-negative) measure \mu on a measurable space (X, \Sigma) is really a function \mu : \Sigma \to , +\infty Therefore, in terms of the usual definition of support, the support of \mu is a subset of the σ-algebra \Sigma: \operatorname (\mu) := \overline, where the overbar denotes set closure. However, this definition is somewhat unsatisfactory: we use the notion of closure, but we do not even have a topology on \Sigma. What we really want to know is where in the space X the measure \mu is non-zero. Consider two examples: # Lebesgue measure \lambda on the real line \Reals. It seems clear that \lambda "lives on" the wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is f(x) = \frac e^\,. The parameter is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma^2 is the variance. The standard deviation of the distribution is (sigma). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stable Distribution
In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it. Of the four parameters defining the family, most attention has been focused on the stability parameter, \alpha (see panel). Stable distributions have 0 < \alpha \leq 2, with the upper bound corresponding to the , and to the Cauchy distribution. The distributio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum Likelihood
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed statistical model, the observed data is most probable. The point in the parameter space that maximizes the likelihood function is called the maximum likelihood estimate. The logic of maximum likelihood is both intuitive and flexible, and as such the method has become a dominant means of statistical inference. If the likelihood function is differentiable, the derivative test for finding maxima can be applied. In some cases, the first-order conditions of the likelihood function can be solved analytically; for instance, the ordinary least squares estimator for a linear regression model maximizes the likelihood when the random errors are assumed to have normal distributions with the same variance. From the perspective of Bayesian inference, ML ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nova Science Publishers, Inc
A nova ( novae or novas) is a transient astronomical event that causes the sudden appearance of a bright, apparently "new" star (hence the name "nova", Latin for "new") that slowly fades over weeks or months. All observed novae involve white dwarfs in close binary systems, but causes of the dramatic appearance of a nova vary, depending on the circumstances of the two progenitor stars. The main sub-classes of novae are classical novae, recurrent novae (RNe), and dwarf novae. They are all considered to be cataclysmic variable stars. Classical nova eruptions are the most common type. This type is usually created in a close binary star system consisting of a white dwarf and either a main sequence, subgiant, or red giant star. If the orbital period of the system is a few days or less, the white dwarf is close enough to its companion star to draw accreted matter onto its surface, creating a dense but shallow atmosphere. This atmosphere, mostly consisting of hydrogen, is heated by t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Progress In Applied Mathematical Modeling
Progress is movement towards a perceived refined, improved, or otherwise desired state. It is central to the philosophy of progressivism, which interprets progress as the set of advancements in technology, science, and social organization efficiency – the latter being generally achieved through direct societal action, as in social enterprise or through activism, but being also attainable through natural sociocultural evolution – that progressivism holds all human societies should strive towards. The concept of progress was introduced in the early-19th-century social theories, especially social evolution as described by Auguste Comte and Herbert Spencer. It was present in the Enlightenment's philosophies of history. As a goal, social progress has been advocated by varying realms of political ideologies with different theories on how it is to be achieved. Measuring progress Specific indicators for measuring progress can range from economic data, technical innovations, chang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canonical Correlation Analysis
In statistics, canonical-correlation analysis (CCA), also called canonical variates analysis, is a way of inferring information from cross-covariance matrices. If we have two vectors ''X'' = (''X''1, ..., ''X''''n'') and ''Y'' = (''Y''1, ..., ''Y''''m'') of random variables, and there are correlations among the variables, then canonical-correlation analysis will find linear combinations of ''X'' and ''Y'' that have a maximum correlation with each other. T. R. Knapp notes that "virtually all of the commonly encountered parametric tests of significance can be treated as special cases of canonical-correlation analysis, which is the general procedure for investigating the relationships between two sets of variables." The method was first introduced by Harold Hotelling in 1936, although in the context of angles between flats the mathematical concept was published by Camille Jordan in 1875. CCA is now a cornerstone of multivariate statistics a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variables
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. The term 'random variable' in its mathematical definition refers to neither randomness nor variability but instead is a mathematical function in which * the domain is the set of possible outcomes in a sample space (e.g. the set \ which are the possible upper sides of a flipped coin heads H or tails T as the result from tossing a coin); and * the range is a measurable space (e.g. corresponding to the domain above, the range might be the set \ if say heads H mapped to -1 and T mapped to 1). Typically, the range of a random variable is a subset of the real numbers. Informally, randomness typically represents some fundamental element of chance, such as in the roll of a die; it may also represent uncertainty, such as measurement error. However, the interpretation of probability is philosophic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for example, the variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical applications is that, unlike the standard deviation, its units differ from the random variable, which is why the standard devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |