|
Invariant Estimator
In statistics, the concept of being an invariant estimator is a criterion that can be used to compare the properties of different estimators for the same quantity. It is a way of formalising the idea that an estimator should have certain intuitively appealing qualities. Strictly speaking, "invariant" would mean that the estimates themselves are unchanged when both the measurements and the parameters are transformed in a compatible way, but the meaning has been extended to allow the estimates to change in appropriate ways with such transformations. The term equivariant estimator is used in formal mathematical contexts that include a precise description of the relation of the way the estimator changes in response to changes to the dataset and parameterisation: this corresponds to the use of " equivariance" in more general mathematics. General setting Background In statistical inference, there are several approaches to estimation theory that can be used to decide immediately what es ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independent And Identically Distributed
Independent or Independents may refer to: Arts, entertainment, and media Artist groups * Independents (artist group), a group of modernist painters based in Pennsylvania, United States * Independentes (English: Independents), a Portuguese artist group Music Groups, labels, and genres * Independent music, a number of genres associated with independent labels * Independent record label, a record label not associated with a major label * Independent Albums, American albums chart Albums * ''Independent'' (Ai album), 2012 * ''Independent'' (Faze album), 2006 * ''Independent'' (Sacred Reich album), 1993 Songs * "Independent" (song), a 2007 song by Webbie * "Independent", a 2002 song by Ayumi Hamasaki from '' H'' News media organizations * Independent Media Center (also known as Indymedia or IMC), an open publishing network of journalist collectives that report on political and social issues, e.g., in ''The Indypendent'' newspaper of NYC * ITV (TV network) (Independent Television ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biometrika
''Biometrika'' is a peer-reviewed scientific journal published by Oxford University Press for the Biometrika Trust. The editor-in-chief is Paul Fearnhead (Lancaster University). The principal focus of this journal is theoretical statistics. It was established in 1901 and originally appeared quarterly. It changed to three issues per year in 1977 but returned to quarterly publication in 1992. History ''Biometrika'' was established in 1901 by Francis Galton, Karl Pearson, and Raphael Weldon to promote the study of biometrics. The history of ''Biometrika'' is covered by Cox (2001). The name of the journal was chosen by Pearson, but Francis Edgeworth insisted that it be spelt with a "k" and not a "c". Since the 1930s, it has been a journal for statistical theory and methodology. Galton's role in the journal was essentially that of a patron and the journal was run by Pearson and Weldon and after Weldon's death in 1906 by Pearson alone until he died in 1936. In the early days, the Ameri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Distribution
The Cauchy distribution, named after Augustin-Louis Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as the Lorentz distribution (after Hendrik Lorentz), Cauchy–Lorentz distribution, Lorentz(ian) function, or Breit–Wigner distribution. The Cauchy distribution f(x; x_0,\gamma) is the distribution of the -intercept of a ray issuing from (x_0,\gamma) with a uniformly distributed angle. It is also the distribution of the Ratio distribution, ratio of two independent Normal distribution, normally distributed random variables with mean zero. The Cauchy distribution is often used in statistics as the canonical example of a "pathological (mathematics), pathological" distribution since both its expected value and its variance are undefined (but see below). The Cauchy distribution does not have finite moment (mathematics), moments of order greater than or equal to one; only fractional absolute moments exist., Chapter 16. The Cauchy dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Normal Distribution
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional ( univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be ''k''-variate normally distributed if every linear combination of its ''k'' components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables, each of which clusters around a mean value. Definitions Notation and parametrization The multivariate normal distribution of a ''k''-dimensional random vector \mathbf = (X_1,\ldots,X_k)^ can be written in the following notation: : \mathbf\ \sim\ \mathcal(\boldsymbol\mu,\, \boldsymbol\Sigma), or to make it explicitly known that \mathb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbit (group Theory)
In mathematics, a group action of a group G on a set S is a group homomorphism from G to some group (under function composition) of functions from S to itself. It is said that G acts on S. Many sets of transformations form a group under function composition; for example, the rotations around a point in the plane. It is often useful to consider the group as an abstract group, and to say that one has a group action of the abstract group that consists of performing the transformations of the group of transformations. The reason for distinguishing the group from the transformations is that, generally, a group of transformations of a structure acts also on various related structures; for example, the above rotation group also acts on triangles by transforming triangles into triangles. If a group acts on a structure, it will usually also act on objects built from that structure. For example, the group of Euclidean isometries acts on Euclidean space and also on the figures draw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equivalence Class
In mathematics, when the elements of some set S have a notion of equivalence (formalized as an equivalence relation), then one may naturally split the set S into equivalence classes. These equivalence classes are constructed so that elements a and b belong to the same equivalence class if, and only if, they are equivalent. Formally, given a set S and an equivalence relation \sim on S, the of an element a in S is denoted /math> or, equivalently, to emphasize its equivalence relation \sim, and is defined as the set of all elements in S with which a is \sim-related. The definition of equivalence relations implies that the equivalence classes form a partition of S, meaning, that every element of the set belongs to exactly one equivalence class. The set of the equivalence classes is sometimes called the quotient set or the quotient space of S by \sim, and is denoted by S /. When the set S has some structure (such as a group operation or a topology) and the equivalence re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Of Transformation
In mathematics, a group action of a group G on a set S is a group homomorphism from G to some group (under function composition) of functions from S to itself. It is said that G acts on S. Many sets of transformations form a group under function composition; for example, the rotations around a point in the plane. It is often useful to consider the group as an abstract group, and to say that one has a group action of the abstract group that consists of performing the transformations of the group of transformations. The reason for distinguishing the group from the transformations is that, generally, a group of transformations of a structure acts also on various related structures; for example, the above rotation group also acts on triangles by transforming triangles into triangles. If a group acts on a structure, it will usually also act on objects built from that structure. For example, the group of Euclidean isometries acts on Euclidean space and also on the figures drawn in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prior Knowledge For Pattern Recognition
Pattern recognition is a very active field of research intimately bound to machine learning. Also known as classification or statistical classification, pattern recognition aims at building a classifier that can determine the class of an input pattern. This procedure, known as training, corresponds to learning an unknown decision function based only on a set of input-output pairs (\boldsymbol_i,y_i) that form the training data (or training set). Nonetheless, in real world applications such as character recognition, a certain amount of information on the problem is usually known beforehand. The incorporation of this prior knowledge into the training is the key element that will allow an increase of performance in many applications. Prior knowledge Prior knowledgeB. Scholkopf and A. Smola,Learning with Kernels, MIT Press 2002. refers to all information about the problem available in addition to the training data. However, in this most general form, determining a model from a finit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Classification
When classification is performed by a computer, statistical methods are normally used to develop the algorithm. Often, the individual observations are analyzed into a set of quantifiable properties, known variously as explanatory variables or ''features''. These properties may variously be categorical (e.g. "A", "B", "AB" or "O", for blood type), ordinal (e.g. "large", "medium" or "small"), integer-valued (e.g. the number of occurrences of a particular word in an email) or real-valued (e.g. a measurement of blood pressure). Other classifiers work by comparing observations to previous observations by means of a similarity or distance function. An algorithm that implements classification, especially in a concrete implementation, is known as a classifier. The term "classifier" sometimes also refers to the mathematical function, implemented by a classification algorithm, that maps input data to a category. Terminology across fields is quite varied. In statistics, where classi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
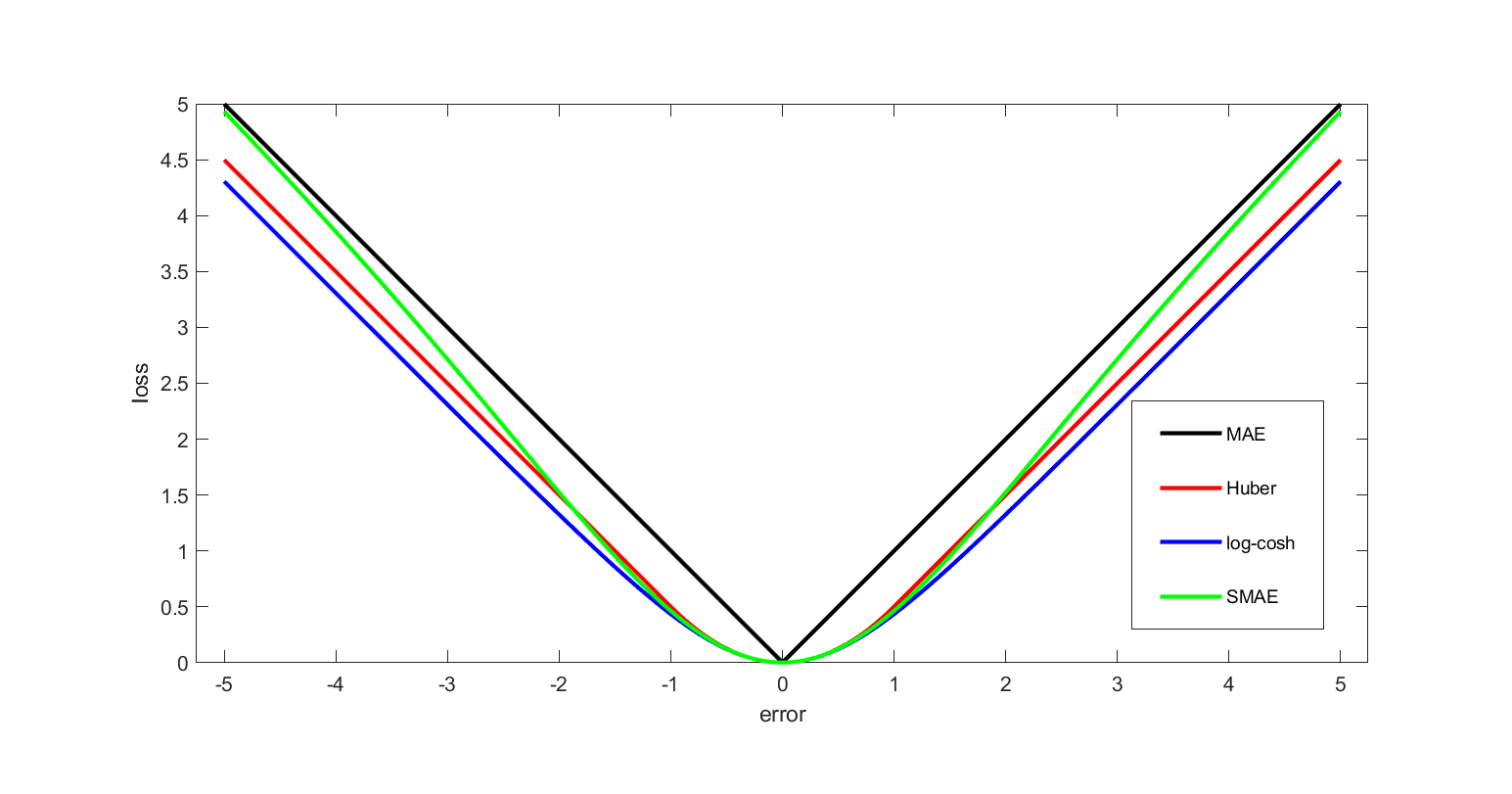
Risk Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economics, for example, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |