|
Pearson X-squared Statistic
Pearson's chi-squared test (\chi^2) is a statistical test applied to sets of categorical data to evaluate how likely it is that any observed difference between the sets arose by chance. It is the most widely used of many chi-squared tests (e.g., Yates, likelihood ratio, portmanteau test in time series, etc.) – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900. In contexts where it is important to improve a distinction between the test statistic and its distribution, names similar to ''Pearson χ-squared'' test or statistic are used. It tests a null hypothesis stating that the frequency distribution of certain events observed in a sample is consistent with a particular theoretical distribution. The events considered must be mutually exclusive and have total probability 1. A common case for this is where the events each cover an outcome of a categorical variable. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Categorical Data
In statistics, a categorical variable (also called qualitative variable) is a variable that can take on one of a limited, and usually fixed, number of possible values, assigning each individual or other unit of observation to a particular group or nominal category on the basis of some qualitative property. In computer science and some branches of mathematics, categorical variables are referred to as enumerations or enumerated types. Commonly (though not in this article), each of the possible values of a categorical variable is referred to as a level. The probability distribution associated with a random categorical variable is called a categorical distribution. Categorical data is the statistical data type consisting of categorical variables or of data that has been converted into that form, for example as grouped data. More specifically, categorical data may derive from observations made of qualitative data that are summarised as counts or cross tabulations, or from observations o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contingency Table
In statistics, a contingency table (also known as a cross tabulation or crosstab) is a type of table in a matrix format that displays the (multivariate) frequency distribution of the variables. They are heavily used in survey research, business intelligence, engineering, and scientific research. They provide a basic picture of the interrelation between two variables and can help find interactions between them. The term ''contingency table'' was first used by Karl Pearson in "On the Theory of Contingency and Its Relation to Association and Normal Correlation", part of the ''Drapers' Company Research Memoirs Biometric Series I'' published in 1904. A crucial problem of multivariate statistics is finding the (direct-)dependence structure underlying the variables contained in high-dimensional contingency tables. If some of the conditional independences are revealed, then even the storage of the data can be done in a smarter way (see Lauritzen (2002)). In order to do this one can use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chi-squared Distribution
In probability theory and statistics, the chi-squared distribution (also chi-square or \chi^2-distribution) with k degrees of freedom is the distribution of a sum of the squares of k independent standard normal random variables. The chi-squared distribution is a special case of the gamma distribution and is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing and in construction of confidence intervals. This distribution is sometimes called the central chi-squared distribution, a special case of the more general noncentral chi-squared distribution. The chi-squared distribution is used in the common chi-squared tests for goodness of fit of an observed distribution to a theoretical one, the independence of two criteria of classification of qualitative data, and in confidence interval estimation for a population standard deviation of a normal distribution from a sample standard deviation. Many other statistical tests a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chi-square DistributionCDF-English
The term chi-square, chi-squared, or \chi^2 has various uses in statistics: *chi-square distribution, a continuous probability distribution *chi-square test A chi-squared test (also chi-square or test) is a statistical hypothesis test used in the analysis of contingency tables when the sample sizes are large. In simpler terms, this test is primarily used to examine whether two categorical variabl ..., name given to some tests using chi-square distribution * chi-square target models, a mathematical model used in radar cross-section {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F-distribution
In probability theory and statistics, the ''F''-distribution or F-ratio, also known as Snedecor's ''F'' distribution or the Fisher–Snedecor distribution (after Ronald Fisher and George W. Snedecor) is a continuous probability distribution that arises frequently as the null distribution of a test statistic, most notably in the analysis of variance (ANOVA) and other ''F''-tests. Definition The F-distribution with ''d''1 and ''d''2 degrees of freedom is the distribution of : X = \frac where S_1 and S_2 are independent random variables with chi-square distributions with respective degrees of freedom d_1 and d_2. It can be shown to follow that the probability density function (pdf) for ''X'' is given by : \begin f(x; d_1,d_2) &= \frac \\ pt&=\frac \left(\frac\right)^ x^ \left(1+\frac \, x \right)^ \end for real ''x'' > 0. Here \mathrm is the beta function. In many applications, the parameters ''d''1 and ''d''2 are positive integers, but the distribution is well-define ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Student's T
In probability and statistics, Student's ''t''-distribution (or simply the ''t''-distribution) is any member of a family of continuous probability distributions that arise when estimating the mean of a normally distributed population in situations where the sample size is small and the population's standard deviation is unknown. It was developed by English statistician William Sealy Gosset under the pseudonym "Student". The ''t''-distribution plays a role in a number of widely used statistical analyses, including Student's ''t''-test for assessing the statistical significance of the difference between two sample means, the construction of confidence intervals for the difference between two population means, and in linear regression analysis. Student's ''t''-distribution also arises in the Bayesian analysis of data from a normal family. If we take a sample of n observations from a normal distribution, then the ''t''-distribution with \nu=n-1 degrees of freedom can be defined ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Gamma Distribution
The generalized gamma distribution is a continuous probability distribution with two shape parameters (and a scale parameter). It is a generalization of the gamma distribution which has one shape parameter (and a scale parameter). Since many distributions commonly used for parametric models in survival analysis (such as the exponential distribution, the Weibull distribution and the gamma distribution) are special cases of the generalized gamma, it is sometimes used to determine which parametric model is appropriate for a given set of data. Another example is the half-normal distribution. Characteristics The generalized gamma distribution has two shape parameters, d > 0 and p > 0, and a scale parameter, a > 0. For non-negative ''x'' from a generalized gamma distribution, the probability density function is : f(x; a, d, p) = \frac, where \Gamma(\cdot) denotes the gamma function. The cumulative distribution function is : F(x; a, d, p) = \frac , where \gamma(\cdot) denotes the lowe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Uniform Distribution
In probability theory and statistics, the discrete uniform distribution is a symmetric probability distribution wherein a finite number of values are equally likely to be observed; every one of ''n'' values has equal probability 1/''n''. Another way of saying "discrete uniform distribution" would be "a known, finite number of outcomes equally likely to happen". A simple example of the discrete uniform distribution is throwing a fair dice. The possible values are 1, 2, 3, 4, 5, 6, and each time the die is thrown the probability of a given score is 1/6. If two dice are thrown and their values added, the resulting distribution is no longer uniform because not all sums have equal probability. Although it is convenient to describe discrete uniform distributions over integers, such as this, one can also consider discrete uniform distributions over any finite set. For instance, a random permutation is a permutation generated uniformly from the permutations of a given length, and a unif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alpha Level
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a "false positive" finding or conclusion; example: "an innocent person is convicted"), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a "false negative" finding or conclusion; example: "a guilty person is not convicted"). Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process. By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased. The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science. Intuitively, type I errors can be thought of as errors of ''commission'', i.e. the researcher unluck ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
P-value
In null-hypothesis significance testing, the ''p''-value is the probability of obtaining test results at least as extreme as the result actually observed, under the assumption that the null hypothesis is correct. A very small ''p''-value means that such an extreme observed outcome would be very unlikely under the null hypothesis. Reporting ''p''-values of statistical tests is common practice in academic publications of many quantitative fields. Since the precise meaning of ''p''-value is hard to grasp, misuse is widespread and has been a major topic in metascience. Basic concepts In statistics, every conjecture concerning the unknown probability distribution of a collection of random variables representing the observed data X in some study is called a ''statistical hypothesis''. If we state one hypothesis only and the aim of the statistical test is to see whether this hypothesis is tenable, but not to investigate other specific hypotheses, then such a test is called a null ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
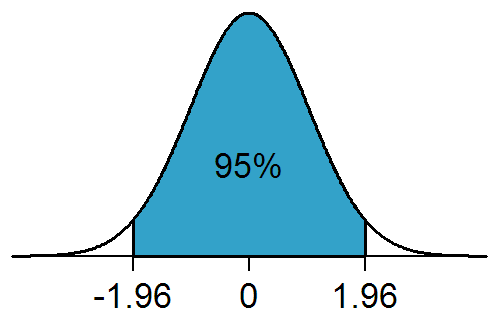
Significance Level
In statistical hypothesis testing, a result has statistical significance when it is very unlikely to have occurred given the null hypothesis (simply by chance alone). More precisely, a study's defined significance level, denoted by \alpha, is the probability of the study rejecting the null hypothesis, given that the null hypothesis is true; and the ''p''-value of a result, ''p'', is the probability of obtaining a result at least as extreme, given that the null hypothesis is true. The result is statistically significant, by the standards of the study, when p \le \alpha. The significance level for a study is chosen before data collection, and is typically set to 5% or much lower—depending on the field of study. In any experiment or observation that involves drawing a sample from a population, there is always the possibility that an observed effect would have occurred due to sampling error alone. But if the ''p''-value of an observed effect is less than (or equal to) the significa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degrees Of Freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary. Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the estimate of a parameter is called the degrees of freedom. In general, the degrees of freedom of an estimate of a parameter are equal to the number of independent scores that go into the estimate minus the number of parameters used as intermediate steps in the estimation of the parameter itself. For example, if the variance is to be estimated from a random sample of ''N'' independent scores, then the degrees of freedom is equal to the number of independent scores (''N'') minus the number of parameters estimated as intermediate steps (one, namely, the sample mean) and is therefore equal to ''N'' − 1. Mathematically, degrees of freedom is the number of dimensions of the domain o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
