|
Pascual Jordan
Ernst Pascual Jordan (; 18 October 1902 – 31 July 1980) was a German theoretical and mathematical physicist who made significant contributions to quantum mechanics and quantum field theory. He contributed much to the mathematical form of matrix mechanics, and developed canonical anticommutation relations for fermions. He introduced Jordan algebras in an effort to formalize quantum field theory; the algebras have since found numerous applications within mathematics. Jordan joined the Nazi Party in 1933, but did not follow the Deutsche Physik movement, which at the time rejected quantum physics developed by Albert Einstein and other Jewish physicists. After the Second World War, he entered politics for the conservative party CDU and served as a member of parliament from 1957 to 1961. Family history and education Jordan was born to Ernst Pasqual Jordan (1858–1924) and Eva Fischer. Ernst Jordan was a painter renowned for his portraits and landscapes. He was an associa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hannover
Hanover (; german: Hannover ; nds, Hannober) is the capital and largest city of the German state of Lower Saxony. Its 535,932 (2021) inhabitants make it the 13th-largest city in Germany as well as the fourth-largest city in Northern Germany after Berlin, Hamburg and Bremen. Hanover's urban area comprises the towns of Garbsen, Langenhagen and Laatzen and has a population of about 791,000 (2018). The Hanover Region has approximately 1.16 million inhabitants (2019). The city lies at the confluence of the River Leine and its tributary the Ihme, in the south of the North German Plain, and is the largest city in the Hannover–Braunschweig–Göttingen–Wolfsburg Metropolitan Region. It is the fifth-largest city in the Low German dialect area after Hamburg, Dortmund, Essen and Bremen. Before it became the capital of Lower Saxony in 1946, Hannover was the capital of the Principality of Calenberg (1636–1692), the Electorate of Hanover (1692–1814), the Kingdom of Han ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canonical Commutation Relation
In quantum mechanics, the canonical commutation relation is the fundamental relation between canonical conjugate quantities (quantities which are related by definition such that one is the Fourier transform of another). For example, hat x,\hat p_x= i\hbar \mathbb between the position operator and momentum operator in the direction of a point particle in one dimension, where is the commutator of and , is the imaginary unit, and is the reduced Planck's constant , and \mathbb is the unit operator. In general, position and momentum are vectors of operators and their commutation relation between different components of position and momentum can be expressed as hat r_i,\hat p_j= i\hbar \delta_ \mathbb. where \delta_ is the Kronecker delta. This relation is attributed to Werner Heisenberg, Max Born and Pascual Jordan (1925), who called it a "quantum condition" serving as a postulate of the theory; it was noted by E. Kennard (1927) to imply the Heisenberg uncertainty princip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Konrad Adenauer Prize
The Konrad Adenauer Prize (german: link=no, Konrad-Adenauer-Preis) was an award by the Germany Foundation, a national conservative organisation associated with the Christian Democratic Union, from 1967 to 2001 It was given annually between 1973 and 1975, then every two years, with exceptions, from 1975 to 2001. It was given to right-wing intellectuals and was named in memory of statesman and former German Chancellor Konrad Adenauer. The journalism and literary prizes are now both separate prizes altogether. This is not to be confused with the Konrad-Adenauer-Preis given by the city of Cologne Cologne ( ; german: Köln ; ksh, Kölle ) is the largest city of the German western state of North Rhine-Westphalia (NRW) and the fourth-most populous city of Germany with 1.1 million inhabitants in the city proper and 3.6 millio .... List of prize winners References {{reflist German awards Konrad Adenauer German literary awards German science and technology a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Max Planck Medal
The Max Planck medal is the highest award of the German Physical Society , the world's largest organization of physicists, for extraordinary achievements in theoretical physics. The prize has been awarded annually since 1929, with few exceptions, and usually to a single person. The winner is awarded with a gold medal and hand-written parchment. In 1943 it was not possible to manufacture the gold medal because the Berlin foundry was hit by a bomb. The board of directors of the German Physical Society decided to manufacture the medals in a substitute metal and to deliver the gold medals later. The highest award of the German Physical Society for outstanding results in experimental physics is the Stern–Gerlach Medal. List of recipients *2023 Rashid A. Sunyaev *2022 Annette Zippelius *2021 Alexander Markovich Polyakov *2020 Andrzej Buras *2019 Detlef Lohse *2018 Juan Ignacio Cirac *2017 Herbert Spohn *2016 Herbert Wagner *2015 Viatcheslav Mukhanov *2014 David Ruelle *2013 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Propagator
In quantum mechanics and quantum field theory, the propagator is a function that specifies the probability amplitude for a particle to travel from one place to another in a given period of time, or to travel with a certain energy and momentum. In Feynman diagrams, which serve to calculate the rate of collisions in quantum field theory, virtual particles contribute their propagator to the rate of the scattering event described by the respective diagram. These may also be viewed as the inverse of the wave operator appropriate to the particle, and are, therefore, often called ''(causal) Green's functions'' (called "''causal''" to distinguish it from the elliptic Laplacian Green's function). Non-relativistic propagators In non-relativistic quantum mechanics, the propagator gives the probability amplitude for a particle to travel from one spatial point (x') at one time (t') to another spatial point (x) at a later time (t). Consider a system with Hamiltonian . The Green's func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jordan–Wigner Transformation
The Jordan–Wigner transformation is a transformation that maps spin operators onto fermionic creation and annihilation operators. It was proposed by Pascual Jordan and Eugene Wigner for one-dimensional lattice models, but now two-dimensional analogues of the transformation have also been created. The Jordan–Wigner transformation is often used to exactly solve 1D spin-chains such as the Ising and XY models by transforming the spin operators to fermionic operators and then diagonalizing in the fermionic basis. This transformation actually shows that the distinction between spin-1/2 particles and fermions is nonexistent. It can be applied to systems with an arbitrary dimension. Analogy between spins and fermions In what follows we will show how to map a 1D spin chain of spin-1/2 particles to fermions. Take spin-1/2 Pauli operators acting on a site j of a 1D chain, \sigma_^, \sigma_^, \sigma_^. Taking the anticommutator of \sigma_^ and \sigma_^, we find \ = I, as would ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jordan Map
In theoretical physics, the Jordan map, often also called the Jordan–Schwinger map is a map from matrices to bilinear expressions of quantum oscillators which expedites computation of representations of Lie algebras occurring in physics. It was introduced by Pascual Jordan in 1935 and was utilized by Julian Schwinger in 1952 to re-work out the theory of quantum angular momentum efficiently, given that map’s ease of organizing the (symmetric) representations of su(2) in Fock space. The map utilizes several creation and annihilation operators a^\dagger_i and a^_i of routine use in quantum field theories and many-body problems, each pair representing a quantum harmonic oscillator. The commutation relations of creation and annihilation operators in a multiple-boson system are, : ^_i, a^\dagger_j\equiv a^_i a^\dagger_j - a^\dagger_ja^_i = \delta_, : ^\dagger_i, a^\dagger_j= ^_i, a^_j= 0, where \ , \ \ /math> is the commutator and \delta_ is the Kronecker delta. These oper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jordan And Einstein Frames
Jordan ( ar, الأردن; tr. ' ), officially the Hashemite Kingdom of Jordan,; tr. ' is a country in Western Asia. It is situated at the crossroads of Asia, Africa, and Europe, within the Levant region, on the East Bank of the Jordan River. Jordan is bordered by Saudi Arabia to the south and east, Iraq to the northeast, Syria to the north, and the Palestinian West Bank, Israel, and the Dead Sea to the west. It has a coastline in its southwest on the Gulf of Aqaba's Red Sea, which separates Jordan from Egypt. Amman is Jordan's capital and largest city, as well as its economic, political, and cultural centre. Modern-day Jordan has been inhabited by humans since the Paleolithic period. Three stable kingdoms emerged there at the end of the Bronze Age: Ammon, Moab and Edom. In the third century BC, the Arab Nabataeans established their Kingdom with Petra as the capital. Later rulers of the Transjordan region include the Assyrian, Babylonian, Roman, Byzantine, Rashidun, Umayy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jordan Algebra
In abstract algebra, a Jordan algebra is a nonassociative algebra over a field whose multiplication satisfies the following axioms: # xy = yx (commutative law) # (xy)(xx) = x(y(xx)) (). The product of two elements ''x'' and ''y'' in a Jordan algebra is also denoted ''x'' ∘ ''y'', particularly to avoid confusion with the product of a related associative algebra. The axioms imply that a Jordan algebra is power-associative, meaning that x^n = x \cdots x is independent of how we parenthesize this expression. They also imply that x^m (x^n y) = x^n(x^m y) for all positive integers ''m'' and ''n''. Thus, we may equivalently define a Jordan algebra to be a commutative, power-associative algebra such that for any element x, the operations of multiplying by powers x^n all commute. Jordan algebras were first introduced by to formalize the notion of an algebra of observables in quantum mechanics. They were originally called "r-number systems", but were renamed "Jordan algebras" by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
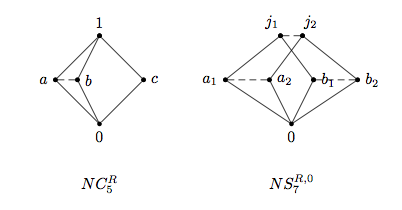
Skew Lattice
In abstract algebra, a skew lattice is an algebraic structure that is a non-commutative generalization of a lattice. While the term ''skew lattice'' can be used to refer to any non-commutative generalization of a lattice, since 1989 it has been used primarily as follows. Definition A skew lattice is a set ''S'' equipped with two associative, idempotent binary operations \wedge and \vee, called ''meet'' and ''join'', that validate the following dual pair of absorption laws x\wedge (x\vee y) = x = (y\vee x)\wedge x , x\vee (x\wedge y) = x = (y\wedge x)\vee x . Given that \vee and \wedge are associative and idempotent, these identities are equivalent to validating the following dual pair of statements: x\vee y= x if x\wedge y=y, x\wedge y=x if x\vee y=y.Leech, J, Skew lattices in rings, Algebra Universalis, 26(1989), 48-72. Historical background For over 60 years, noncommutative variations of lattices have been studied with differing motivations. For some the motivation h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg)