|
Palindrome Number
A palindromic number (also known as a numeral palindrome or a numeric palindrome) is a number (such as 16461) that remains the same when its digits are reversed. In other words, it has reflectional symmetry across a vertical axis. The term ''palindromic'' is derived from palindrome, which refers to a word (such as ''rotor'' or ''racecar'') whose spelling is unchanged when its letters are reversed. The first 30 palindromic numbers (in decimal) are: : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, 33, 44, 55, 66, 77, 88, 99, 101, 111, 121, 131, 141, 151, 161, 171, 181, 191, 202, … . Palindromic numbers receive most attention in the realm of recreational mathematics. A typical problem asks for numbers that possess a certain property ''and'' are palindromic. For instance: * The palindromic primes are 2, 3, 5, 7, 11, 101, 131, 151, ... . * The palindromic square numbers are 0, 1, 4, 9, 121, 484, 676, 10201, 12321, ... . It is obvious that in any base there are infinitely many palindro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reflectional Symmetry
In mathematics, reflection symmetry, line symmetry, mirror symmetry, or mirror-image symmetry is symmetry with respect to a reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry. In 2D there is a line/axis of symmetry, in 3D a plane of symmetry. An object or figure which is indistinguishable from its transformed image is called mirror symmetric. In conclusion, a line of symmetry splits the shape in half and those halves should be identical. Symmetric function In formal terms, a mathematical object is symmetric with respect to a given operation such as reflection, rotation or translation, if, when applied to the object, this operation preserves some property of the object. The set of operations that preserve a given property of the object form a group. Two objects are symmetric to each other with respect to a given group of operations if one is obtained from the other by some of the operations (and vice versa). The symm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Odd Number
In mathematics, parity is the property of an integer of whether it is even or odd. An integer is even if it is a multiple of two, and odd if it is not.. For example, −4, 0, 82 are even because \begin -2 \cdot 2 &= -4 \\ 0 \cdot 2 &= 0 \\ 41 \cdot 2 &= 82 \end By contrast, −3, 5, 7, 21 are odd numbers. The above definition of parity applies only to integer numbers, hence it cannot be applied to numbers like 1/2 or 4.201. See the section "Higher mathematics" below for some extensions of the notion of parity to a larger class of "numbers" or in other more general settings. Even and odd numbers have opposite parities, e.g., 22 (even number) and 13 (odd number) have opposite parities. In particular, the parity of zero is even. Any two consecutive integers have opposite parity. A number (i.e., integer) expressed in the decimal numeral system is even or odd according to whether its last digit is even or odd. That is, if the last digit is 1, 3, 5, 7, or 9, then it is odd; otherwis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mersenne Prime
In mathematics, a Mersenne prime is a prime number that is one less than a power of two. That is, it is a prime number of the form for some integer . They are named after Marin Mersenne, a French Minim friar, who studied them in the early 17th century. If is a composite number then so is . Therefore, an equivalent definition of the Mersenne primes is that they are the prime numbers of the form for some prime . The exponents which give Mersenne primes are 2, 3, 5, 7, 13, 17, 19, 31, ... and the resulting Mersenne primes are 3, 7, 31, 127, 8191, 131071, 524287, 2147483647, ... . Numbers of the form without the primality requirement may be called Mersenne numbers. Sometimes, however, Mersenne numbers are defined to have the additional requirement that be prime. The smallest composite Mersenne number with prime exponent ''n'' is . Mersenne primes were studied in antiquity because of their close connection to perfect numbers: the Euclid–Euler theorem as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermat Prime
In mathematics, a Fermat number, named after Pierre de Fermat, who first studied them, is a positive integer of the form :F_ = 2^ + 1, where ''n'' is a non-negative integer. The first few Fermat numbers are: : 3, 5, 17, 257, 65537, 4294967297, 18446744073709551617, ... . If 2''k'' + 1 is prime and ''k'' > 0, then ''k'' must be a power of 2, so 2''k'' + 1 is a Fermat number; such primes are called Fermat primes. , the only known Fermat primes are ''F''0 = 3, ''F''1 = 5, ''F''2 = 17, ''F''3 = 257, and ''F''4 = 65537 ; heuristics suggest that there are no more. Basic properties The Fermat numbers satisfy the following recurrence relations: : F_ = (F_-1)^+1 : F_ = F_ \cdots F_ + 2 for ''n'' ≥ 1, : F_ = F_ + 2^F_ \cdots F_ : F_ = F_^2 - 2(F_-1)^2 for ''n'' ≥ 2. Each of these relations can be proved by mathematical induction. From the second equation, we can deduce Goldbach's theorem (named after Christian Goldbach): no two Fermat numbers share a common integer factor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Numeral System
A binary number is a number expressed in the base-2 numeral system or binary numeral system, a method of mathematical expression which uses only two symbols: typically "0" (zero) and "1" ( one). The base-2 numeral system is a positional notation with a radix of 2. Each digit is referred to as a bit, or binary digit. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used by almost all modern computers and computer-based devices, as a preferred system of use, over various other human techniques of communication, because of the simplicity of the language and the noise immunity in physical implementation. History The modern binary number system was studied in Europe in the 16th and 17th centuries by Thomas Harriot, Juan Caramuel y Lobkowitz, and Gottfried Leibniz. However, systems related to binary numbers have appeared earlier in multiple cultures including ancient Egypt, China, and India. Leibniz was specifica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourth Power
In arithmetic and algebra, the fourth power of a number ''n'' is the result of multiplying four instances of ''n'' together. So: :''n''4 = ''n'' × ''n'' × ''n'' × ''n'' Fourth powers are also formed by multiplying a number by its cube. Furthermore, they are squares of squares. The sequence of fourth powers of integers (also known as biquadrates or tesseractic numbers) is: :0, 1, 16, 81, 256, 625, 1296, 2401, 4096, 6561, 10000, 14641, 20736, 28561, 38416, 50625, 65536, 83521, 104976, 130321, 160000, 194481, 234256, 279841, 331776, 390625, 456976, 531441, 614656, 707281, 810000, ... . Properties The last digit of a fourth power in decimal can only be 0 (in fact 0000), 1, 5 (in fact 0625), or 6. Every positive integer can be expressed as the sum of at most 19 fourth powers; every integer larger than 13792 can be expressed as the sum of at most 16 fourth powers (see Waring's problem). Fermat knew that a fourth power cannot be the sum of two other fourth powers (the ''n'' = 4 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Number
In mathematics, a square number or perfect square is an integer that is the square (algebra), square of an integer; in other words, it is the multiplication, product of some integer with itself. For example, 9 is a square number, since it equals and can be written as . The usual notation for the square of a number is not the product , but the equivalent exponentiation , usually pronounced as " squared". The name ''square'' number comes from the name of the shape. The unit of area is defined as the area of a unit square (). Hence, a square with side length has area . If a square number is represented by ''n'' points, the points can be arranged in rows as a square each side of which has the same number of points as the square root of ''n''; thus, square numbers are a type of figurate numbers (other examples being Cube (algebra), cube numbers and triangular numbers). Square numbers are non-negative. A non-negative integer is a square number when its square root is again an intege ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
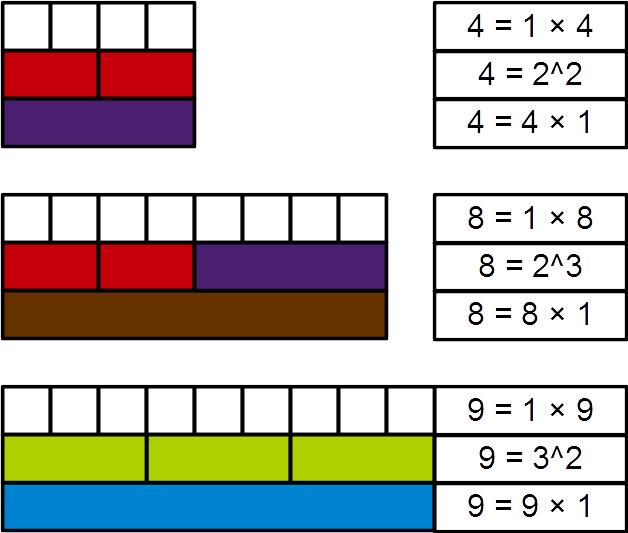
Perfect Power
In mathematics, a perfect power is a natural number that is a product of equal natural factors, or, in other words, an integer that can be expressed as a square or a higher integer power of another integer greater than one. More formally, ''n'' is a perfect power if there exist natural numbers ''m'' > 1, and ''k'' > 1 such that ''mk'' = ''n''. In this case, ''n'' may be called a perfect ''k''th power. If ''k'' = 2 or ''k'' = 3, then ''n'' is called a perfect square or perfect cube, respectively. Sometimes 0 and 1 are also considered perfect powers (0''k'' = 0 for any ''k'' > 0, 1''k'' = 1 for any ''k''). Examples and sums A sequence of perfect powers can be generated by iterating through the possible values for ''m'' and ''k''. The first few ascending perfect powers in numerical order (showing duplicate powers) are : : 2^2 = 4,\ 2^3 = 8,\ 3^2 = 9,\ 2^4 = 16,\ 4^2 = 16,\ 5^2 = 25,\ 3^3 = 27, 2^5 = 32,\ 6^2 = 36,\ 7^2 = 49,\ 2^6 = 64,\ 4^3 = 64,\ 8^2 = 64, \dots The sum of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divisor Function
In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as ''the'' divisor function, it counts the ''number of divisors of an integer'' (including 1 and the number itself). It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important Modular arithmetic, congruences and identity (mathematics), identities; these are treated separately in the article Ramanujan's sum. A related function is the divisor summatory function, which, as the name implies, is a sum over the divisor function. Definition The sum of positive divisors function σ''z''(''n''), for a real or complex number ''z'', is defined as the summation, sum of the ''z''th Exponentiation, powers of the positive divisors of ''n''. It can be expressed in Summation#Capital ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carmichael Number
In number theory, a Carmichael number is a composite number n, which in modular arithmetic satisfies the congruence relation: :b^n\equiv b\pmod for all integers b. The relation may also be expressed in the form: :b^\equiv 1\pmod. for all integers b which are relatively prime to n. Carmichael numbers are named after American mathematician Robert Carmichael, the term having been introduced by Nicolaas Beeger in 1950 ( Øystein Ore had referred to them in 1948 as numbers with the "Fermat property", or "''F'' numbers" for short). They are infinite in number. They constitute the comparatively rare instances where the strict converse of Fermat's Little Theorem does not hold. This fact precludes the use of that theorem as an absolute test of primality. The Carmichael numbers form the subset ''K''1 of the Knödel numbers. Overview Fermat's little theorem states that if ''p'' is a prime number, then for any integer ''b'', the number ''b'' − ''b'' is an integer multipl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Factor
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number n, called trial division, tests whether n is a multiple of any integer between 2 and \sqrt. Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Möbius Function
The Möbius function is a multiplicative function in number theory introduced by the German mathematician August Ferdinand Möbius (also transliterated ''Moebius'') in 1832. It is ubiquitous in elementary and analytic number theory and most often appears as part of its namesake the Möbius inversion formula. Following work of Gian-Carlo Rota in the 1960s, generalizations of the Möbius function were introduced into combinatorics, and are similarly denoted . Definition For any positive integer , define as the sum of the primitive th roots of unity. It has values in depending on the factorization of into prime factors: * if is a square-free positive integer with an even number of prime factors. * if is a square-free positive integer with an odd number of prime factors. * if has a squared prime factor. The Möbius function can alternatively be represented as : \mu(n) = \delta_ \lambda(n), where is the Kronecker delta, is the Liouville function, is the number of dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
