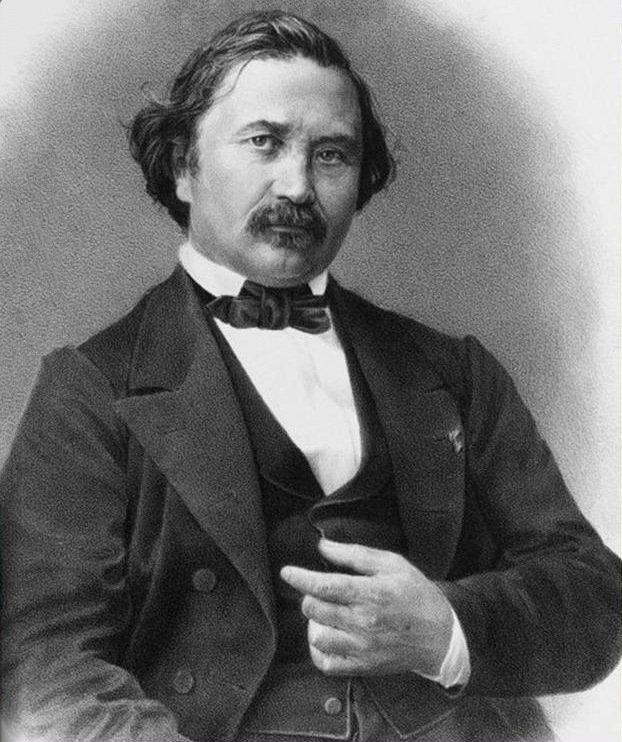|
Pafnuty Chebyschev
Pafnuty Lvovich Chebyshev ( rus, Пафну́тий Льво́вич Чебышёв, p=pɐfˈnutʲɪj ˈlʲvovʲɪtɕ tɕɪbɨˈʂof) ( – ) was a Russian mathematician and considered to be the founding father of Russian mathematics. Chebyshev is known for his fundamental contributions to the fields of probability, statistics, mechanics, and number theory. A number of important mathematical concepts are named after him, including the Chebyshev inequality (which can be used to prove the weak law of large numbers), the Bertrand–Chebyshev theorem, Chebyshev polynomials, Chebyshev linkage, and Chebyshev bias. Transcription The surname Chebyshev has been transliterated in several different ways, like Tchebichef, Tchebychev, Tchebycheff, Tschebyschev, Tschebyschef, Tschebyscheff, Čebyčev, Čebyšev, Chebysheff, Chebychov, Chebyshov (according to native Russian speakers, this one provides the closest pronunciation in English to the correct pronunciation in old Rus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zhukovsky District, Kaluga Oblast
Zhukovsky District (russian: Жуковский райо́н) is an administrativeCharter of Kaluga Oblast and municipalLaw #7-OZ district (raion), one of the twenty-four in Kaluga Oblast, Russia. It is located in the northeast of the oblast. The area of the district is . Its administrative center is the town of Zhukov Georgy Konstantinovich Zhukov ( rus, Георгий Константинович Жуков, p=ɡʲɪˈorɡʲɪj kənstɐnʲˈtʲinəvʲɪtɕ ˈʐukəf, a=Ru-Георгий_Константинович_Жуков.ogg; 1 December 1896 – .... Population: 46,180 ( 2002 Census); The population of Zhukov accounts for 26.0% of the district's total population. References Notes Sources * * {{Use mdy dates, date=February 2013 Districts of Kaluga Oblast ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics."German original: "Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik." Number theorists study prime numbers as well as the properties of mathematical objects made out of integers (for example, rational numbers) or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of Complex analysis, analytical objects (for example, the Riemann zeta function) that encode properties of the integers, primes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ISO 9
ISO 9 is an international standard establishing a system for the transliteration into Latin characters of Cyrillic characters constituting the alphabets of many Slavic and non-Slavic languages. Published on February 23, 1995 by the International Organization for Standardization, the major advantage ISO 9 has over other competing systems is its univocal system of one character for one character equivalents (by the use of diacritics), which faithfully represents the original spelling and allows for reverse transliteration, even if the language is unknown. Earlier versions of the standard, ISO/R 9:1954, ISO/R 9:1968 and ISO 9:1986, were more closely based on the international scholarly system for linguistics (scientific transliteration), but have diverged in favour of unambiguous transliteration over phonemic representation. The edition of 1995 supersedes the edition of 1986. ISO 9:1995 The standard features three mapping tables: the first covers contemporary Slavic languages, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transliteration
Transliteration is a type of conversion of a text from one writing system, script to another that involves swapping Letter (alphabet), letters (thus ''wikt:trans-#Prefix, trans-'' + ''wikt:littera#Latin, liter-'') in predictable ways, such as Greek → , Cyrillic → , Greek → the digraph , Armenian → or Latin → . For instance, for the Greek language, Modern Greek term "", which is usually Translation, translated as "Greece, Hellenic Republic", the usual transliteration to Latin script is , and the name for Russia in Cyrillic script, "", is Scientific transliteration of Cyrillic, usually transliterated as . Transliteration is not primarily concerned with representing the Phonetics, sounds of the original but rather with representing the characters, ideally accurately and unambiguously. Thus, in the Greek above example, is transliterated though it is pronounced , is transliterated though pronounced , and is transliterated , though it is pronounced (exactly li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Romanization Of Russian
The romanization of the Russian language (the transliteration of Russian text from the Cyrillic script into the Latin script), aside from its primary use for including Russian names and words in text written in a Latin alphabet, is also essential for computer users to input Russian text who either do not have a keyboard or word processor set up for inputting Cyrillic, or else are not capable of typing rapidly using a Keyboard layout#Russian, native Russian keyboard layout (JCUKEN). In the latter case, they would type using a system of transliteration fitted for their keyboard layout, such as for English QWERTY keyboards, and then use an automated tool to convert the text into Cyrillic. Systematic transliterations of Cyrillic to Latin There are a number of distinct and competing standards for the romanization of Russian Cyrillic, with none of them having received much popularity, and, in reality, transliteration is often carried out without any consistent standards. Scientific tr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chebyshev Bias
In number theory, Chebyshev's bias is the phenomenon that most of the time, there are more primes of the form 4''k'' + 3 than of the form 4''k'' + 1, up to the same limit. This phenomenon was first observed by Russian mathematician Pafnuty Chebyshev in 1853. Description Let π(''x''; ''n'', ''m'') denote the number of primes of the form ''nk'' + ''m'' up to ''x''. By the prime number theorem (extended to arithmetic progression), :\pi(x;4,1)\sim\pi(x;4,3)\sim \frac\frac. That is, half of the primes are of the form 4''k'' + 1, and half of the form 4''k'' + 3. A reasonable guess would be that π(''x''; 4, 1) > π(''x''; 4, 3) and π(''x''; 4, 1) < π(''x''; 4, 3) each also occur 50% of the time. This, however, is not supported by numerical evidence — in fact, π(''x''; 4, 3) > π(''x''; 4, 1) occurs much more frequently. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chebyshev Linkage
In kinematics, Chebyshev's linkage is a four-bar linkage that converts rotational motion to approximate linear motion. It was invented by the 19th-century mathematician Pafnuty Chebyshev, who studied theoretical problems in kinematic mechanisms. One of the problems was the construction of a linkage that converts a rotary motion into an approximate straight-line motion (a straight line mechanism). This was also studied by James Watt in his improvements to the steam engine, which resulted in Watt's linkage. – Cross link straight-line mechanism Equations of motion The motion of the linkage can be constrained to an input angle that may be changed through velocities, forces, etc. The input angles can be either link ''L''2 with the horizontal or link ''L''4 with the hori ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chebyshev Polynomial
The Chebyshev polynomials are two sequences of polynomials related to the cosine and sine functions, notated as T_n(x) and U_n(x). They can be defined in several equivalent ways, one of which starts with trigonometric functions: The Chebyshev polynomials of the first kind T_n are defined by : T_n(\cos \theta) = \cos(n\theta). Similarly, the Chebyshev polynomials of the second kind U_n are defined by : U_n(\cos \theta) \sin \theta = \sin\big((n + 1)\theta\big). That these expressions define polynomials in \cos\theta may not be obvious at first sight, but follows by rewriting \cos(n\theta) and \sin\big((n+1)\theta\big) using de Moivre's formula or by using the angle sum formulas for \cos and \sin repeatedly. For example, the double angle formulas, which follow directly from the angle sum formulas, may be used to obtain T_2(\cos\theta)=\cos(2\theta)=2\cos^2\theta-1 and U_1(\cos\theta)\sin\theta=\sin(2\theta)=2\cos\theta\sin\theta, which are respectively a polynomial in \cos\th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bertrand's Postulate
In number theory, Bertrand's postulate is a theorem stating that for any integer n > 3, there always exists at least one prime number p with :n < p < 2n - 2. A less restrictive formulation is: for every , there is always at least one prime such that : Another formulation, where is the -th prime, is: for : This statement was first d in 1845 by (1822–1900). Bertrand himself verified his statement for all integers . His conjecture was completely [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weak Law Of Large Numbers
In probability theory, the law of large numbers (LLN) is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value and tends to become closer to the expected value as more trials are performed. The LLN is important because it guarantees stable long-term results for the averages of some random events. For example, while a casino may lose money in a single spin of the roulette wheel, its earnings will tend towards a predictable percentage over a large number of spins. Any winning streak by a player will eventually be overcome by the parameters of the game. Importantly, the law applies (as the name indicates) only when a ''large number'' of observations are considered. There is no principle that a small number of observations will coincide with the expected value or that a streak of one value will immediately be "balanced ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chebyshev Inequality
In probability theory, Chebyshev's inequality (also called the Bienaymé–Chebyshev inequality) guarantees that, for a wide class of probability distributions, no more than a certain fraction of values can be more than a certain distance from the mean. Specifically, no more than 1/''k''2 of the distribution's values can be ''k'' or more standard deviations away from the mean (or equivalently, at least 1 − 1/''k''2 of the distribution's values are less than ''k'' standard deviations away from the mean). The rule is often called Chebyshev's theorem, about the range of standard deviations around the mean, in statistics. The inequality has great utility because it can be applied to any probability distribution in which the mean and variance are defined. For example, it can be used to prove the weak law of large numbers. Its practical usage is similar to the 68–95–99.7 rule, which applies only to normal distributions. Chebyshev's inequality is more general, stating th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems. Mathematicians are concerned with numbers, data, quantity, structure, space, models, and change. History One of the earliest known mathematicians were Thales of Miletus (c. 624–c.546 BC); he has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales' Theorem. The number of known mathematicians grew when Pythagoras of Samos (c. 582–c. 507 BC) established the Pythagorean School, whose doctrine it was that mathematics ruled the universe and whose motto was "All is number". It was the Pythagoreans who coined the term "mathematics", and with whom the study of mathematics for its own sake begins. The first woman mathematician recorded by history was Hypati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |