|
Overlap–save Method
In signal processing, ''overlap–save'' is the traditional name for an efficient way to evaluate the Convolution#Discrete convolution, discrete convolution between a very long signal x[n] and a finite impulse response (FIR) filter h[n]: where for ''m'' outside the region . This article uses common abstract notations, such as y(t) = x(t) * h(t), or y(t) = \mathcal\, in which it is understood that the functions should be thought of in their totality, rather than at specific instants t (see Convolution#Notation). The concept is to compute short segments of ''y''[''n''] of an arbitrary length ''L'', and concatenate the segments together. Consider a segment that begins at ''n'' = ''kL'' + ''M'', for any integer ''k'', and define: :x_k[n] \ \triangleq \begin x[n+kL], & 1 \le n \le L+M-1\\ 0, & \textrm. \end :y_k[n] \ \triangleq \ x_k[n]*h[n] = \sum_^ h[m] \cdot x_k[n-m]. Then, for kL+M+1 \le n \le kL+L+M, and equivalently M+1 \le n-kL \le L+M, we can write: :y[n] = \su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital re ...
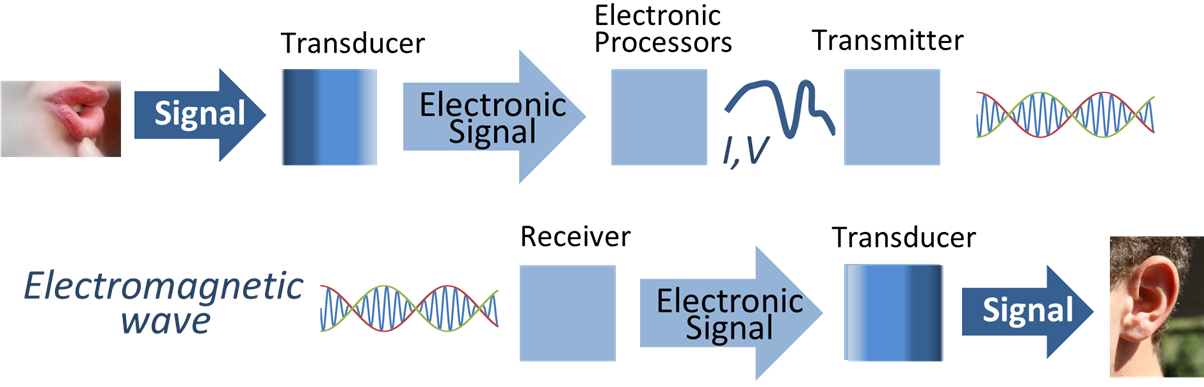
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing '' signals'', such as sound, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, digital storage efficiency, correcting distorted signals, subjective video quality and to also detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim Alan Victor Oppenheim''Alan Victor Oppenheim'' was elected in 1987 [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution
In mathematics (in particular, functional analysis), convolution is a mathematical operation on two functions ( and ) that produces a third function (f*g) that expresses how the shape of one is modified by the other. The term ''convolution'' refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The choice of which function is reflected and shifted before the integral does not change the integral result (see commutativity). The integral is evaluated for all values of shift, producing the convolution function. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution (f*g) differs from cross-correlation (f \star g) only in that either or is reflected about the y-axis in convolution; thus it is a cross-correlation of and , or and . For complex-valued fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Impulse Response
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response (or response to any finite length input) is of ''finite'' duration, because it settles to zero in finite time. This is in contrast to infinite impulse response (IIR) filters, which may have internal feedback and may continue to respond indefinitely (usually decaying). The impulse response (that is, the output in response to a Kronecker delta input) of an Nth-order discrete-time FIR filter lasts exactly N+1 samples (from first nonzero element through last nonzero element) before it then settles to zero. FIR filters can be discrete-time or continuous-time, and digital or analog. Definition For a causal discrete-time FIR filter of order ''N'', each value of the output sequence is a weighted sum of the most recent input values: :\begin y &= b_0 x + b_1 x -1+ \cdots + b_N x -N\\ &= \sum_^N b_i\cdot x -i \end where: * x /math> is the input signal, * y /math> is the output ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Convolution
Circular convolution, also known as cyclic convolution, is a special case of periodic convolution, which is the convolution of two periodic functions that have the same period. Periodic convolution arises, for example, in the context of the discrete-time Fourier transform (DTFT). In particular, the DTFT of the product of two discrete sequences is the periodic convolution of the DTFTs of the individual sequences. And each DTFT is a periodic summation of a continuous Fourier transform function (see ). Although DTFTs are usually continuous functions of frequency, the concepts of periodic and circular convolution are also directly applicable to discrete sequences of data. In that context, circular convolution plays an important role in maximizing the efficiency of a certain kind of common filtering operation. Definitions The ''periodic convolution'' of two T-periodic functions, h_(t) and x_(t) can be defined as: :\int_^ h_(\tau)\cdot x_(t - \tau)\,d\tau, where ''t''o is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Fourier Transform
In mathematics, the discrete Fourier transform (DFT) converts a finite sequence of equally-spaced Sampling (signal processing), samples of a function (mathematics), function into a same-length sequence of equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a complex number, complex-valued function of frequency. The interval at which the DTFT is sampled is the reciprocal of the duration of the input sequence. An inverse DFT is a Fourier series, using the DTFT samples as coefficients of complex number, complex Sine wave, sinusoids at the corresponding DTFT frequencies. It has the same sample-values as the original input sequence. The DFT is therefore said to be a frequency domain representation of the original input sequence. If the original sequence spans all the non-zero values of a function, its DTFT is continuous (and periodic), and the DFT provides discrete samples of one cycle. If the original sequence is one cycle of a periodic function, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fast Fourier Transform
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). Fourier analysis converts a signal from its original domain (often time or space) to a representation in the frequency domain and vice versa. The DFT is obtained by decomposing a sequence of values into components of different frequencies. This operation is useful in many fields, but computing it directly from the definition is often too slow to be practical. An FFT rapidly computes such transformations by factorizing the DFT matrix into a product of sparse (mostly zero) factors. As a result, it manages to reduce the complexity of computing the DFT from O\left(N^2\right), which arises if one simply applies the definition of DFT, to O(N \log N), where N is the data size. The difference in speed can be enormous, especially for long data sets where ''N'' may be in the thousands or millions. In the presence of round-off error, many FFT algorith ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
FFT Size Vs Filter Length For Overlap-add Convolution
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). Fourier analysis converts a signal from its original domain (often time or space) to a representation in the frequency domain and vice versa. The DFT is obtained by decomposing a sequence of values into components of different frequencies. This operation is useful in many fields, but computing it directly from the definition is often too slow to be practical. An FFT rapidly computes such transformations by factorizing the DFT matrix into a product of sparse (mostly zero) factors. As a result, it manages to reduce the complexity of computing the DFT from O\left(N^2\right), which arises if one simply applies the definition of DFT, to O(N \log N), where N is the data size. The difference in speed can be enormous, especially for long data sets where ''N'' may be in the thousands or millions. In the presence of round-off error, many FFT algorithms ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Overlap–add Method
In signal processing, the overlap–add method is an efficient way to evaluate the discrete convolution of a very long signal x /math> with a finite impulse response (FIR) filter h /math>: where for ''m'' outside the region . This article uses common abstract notations, such as y(t) = x(t) * h(t), or y(t) = \mathcal\, in which it is understood that the functions should be thought of in their totality, rather than at specific instants t (see Convolution#Notation). The concept is to divide the problem into multiple convolutions of ''h'' 'n''with short segments of x /math>: :x_k \triangleq\ \begin x + kL & n = 1, 2, \ldots, L\\ 0, & \text, \end where ''L'' is an arbitrary segment length. Then: :x = \sum_ x_k - kL\, and ''y'' 'n''can be written as a sum of short convolutions: :\begin y = \left(\sum_ x_k - kLright) * h &= \sum_ \left(x_k - kL* h right)\\ &= \sum_ y_k - kL \end where the linear convolution y_k \triangleq\ x_k * h , is zero outsid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital re ...
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing '' signals'', such as sound, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, digital storage efficiency, correcting distorted signals, subjective video quality and to also detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim Alan Victor Oppenheim''Alan Victor Oppenheim'' was elected in 1987 [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |