|
Ordinal Data
Ordinal data is a categorical, statistical data type where the variables have natural, ordered categories and the distances between the categories are not known. These data exist on an ordinal scale, one of four levels of measurement described by S. S. Stevens in 1946. The ordinal scale is distinguished from the nominal scale by having a ''ranking''. It also differs from the interval scale and ratio scale by not having category widths that represent equal increments of the underlying attribute. Examples of ordinal data A well-known example of ordinal data is the Likert scale. An example of a Likert scale is: Examples of ordinal data are often found in questionnaires: for example, the survey question "Is your general health poor, reasonable, good, or excellent?" may have those answers coded respectively as 1, 2, 3, and 4. Sometimes data on an interval scale or ratio scale are grouped onto an ordinal scale: for example, individuals whose income is known might be grouped into the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Data Type
In statistics, groups of individual data points may be classified as belonging to any of various statistical data types, e.g. categorical ("red", "blue", "green"), real number (1.68, -5, 1.7e+6), odd number (1,3,5) etc. The data type is a fundamental component of the semantic content of the variable, and controls which sorts of probability distributions can logically be used to describe the variable, the permissible operations on the variable, the type of regression analysis used to predict the variable, etc. The concept of data type is similar to the concept of level of measurement, but more specific: For example, count data require a different distribution (e.g. a Poisson distribution or binomial distribution) than non-negative real-valued data require, but both fall under the same level of measurement (a ratio scale). Various attempts have been made to produce a taxonomy of levels of measurement. The psychophysicist Stanley Smith Stevens defined nominal, ordinal, interva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kruskal–Wallis One-way Analysis Of Variance
The Kruskal–Wallis test by ranks, Kruskal–Wallis ''H'' testKruskal–Wallis H Test using SPSS Statistics Laerd Statistics (named after William Kruskal and ), or one-way ANOVA on ranks is a non-parametric method for testing whether samples originate from the same distribution. It is used for comparing two or more independent samples of equal or different sample sizes. It extends the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordered Probit
In statistics, ordered probit is a generalization of the widely used probit analysis to the case of more than two outcomes of an ordinal dependent variable (a dependent variable for which the potential values have a natural ordering, as in poor, fair, good, excellent). Similarly, the widely used logit method also has a counterpart ordered logit. Ordered probit, like ordered logit, is a particular method of ordinal regression. For example, in clinical research, the effect a drug may have on a patient may be modeled with ordered probit regression. Independent variables may include the use or non-use of the drug as well as control variables such as age and details from medical history such as whether the patient suffers from high blood pressure, heart disease, etc. The dependent variable would be ranked from the following list: complete cure, relieve symptoms, no effect, deteriorate condition, death. Another example application are Likert-type items commonly employed in survey res ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordered Logit
In statistics, the ordered logit model (also ordered logistic regression or proportional odds model) is an ordinal regression model—that is, a regression model for ordinal dependent variables—first considered by Peter McCullagh. For example, if one question on a survey is to be answered by a choice among "poor", "fair", "good", "very good" and "excellent", and the purpose of the analysis is to see how well that response can be predicted by the responses to other questions, some of which may be quantitative, then ordered logistic regression may be used. It can be thought of as an extension of the logistic regression model that applies to dichotomous dependent variables, allowing for more than two (ordered) response categories. The model and the proportional odds assumption The model only applies to data that meet the ''proportional odds assumption'', the meaning of which can be exemplified as follows. Suppose there are five outcomes: "poor", "fair", "good", "very good", a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinal Regression
In statistics, ordinal regression, also called ordinal classification, is a type of regression analysis used for predicting an ordinal variable, i.e. a variable whose value exists on an arbitrary scale where only the relative ordering between different values is significant. It can be considered an intermediate problem between regression and classification. Examples of ordinal regression are ordered logit and ordered probit. Ordinal regression turns up often in the social sciences, for example in the modeling of human levels of preference (on a scale from, say, 1–5 for "very poor" through "excellent"), as well as in information retrieval. In machine learning, ordinal regression may also be called ranking learning. Linear models for ordinal regression Ordinal regression can be performed using a generalized linear model (GLM) that fits both a coefficient vector and a set of ''thresholds'' to a dataset. Suppose one has a set of observations, represented by length- vectors thr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dependent Variable
Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, in turn, are not seen as depending on any other variable in the scope of the experiment in question. In this sense, some common independent variables are time, space, density, mass, fluid flow rate, and previous values of some observed value of interest (e.g. human population size) to predict future values (the dependent variable). Of the two, it is always the dependent variable whose variation is being studied, by altering inputs, also known as regressors in a statistical context. In an experiment, any variable that can be attributed a value without attributing a value to any other variable is called a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
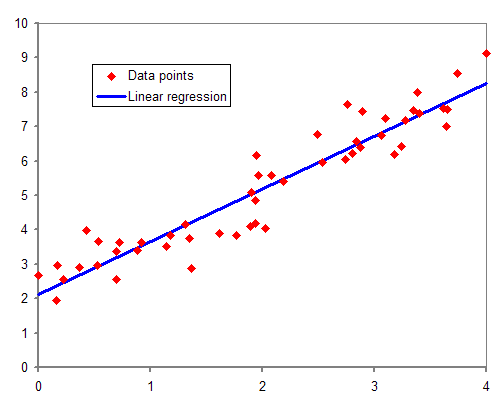
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logistic Regression
In statistics, the logistic model (or logit model) is a statistical model that models the probability of an event taking place by having the log-odds for the event be a linear function (calculus), linear combination of one or more independent variables. In regression analysis, logistic regression (or logit regression) is estimation theory, estimating the parameters of a logistic model (the coefficients in the linear combination). Formally, in binary logistic regression there is a single binary variable, binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable (two classes, coded by an indicator variable) or a continuous variable (any real value). The corresponding probability of the value labeled "1" can vary between 0 (certainly the value "0") and 1 (certainly the value "1"), hence the labeling; the function that converts log-odds to probability is the logistic function, h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Somers' D
In statistics, Somers’ ''D'', sometimes incorrectly referred to as Somer’s ''D'', is a measure of ordinal association between two possibly dependent random variables and . Somers’ ''D'' takes values between -1 when all pairs of the variables disagree and 1 when all pairs of the variables agree. Somers’ ''D'' is named after Robert H. Somers, who proposed it in 1962. Somers’ ''D'' plays a central role in rank statistics and is the parameter behind many nonparametric methods. It is also used as a quality measure of binary choice or ordinal regression (e.g., logistic regressions) and credit scoring models. Somers’ ''D'' for sample We say that two pairs (x_i,y_i) and (x_j,y_j) are concordant if the ranks of both elements agree, or x_i>x_j and y_i>y_j or if x_i |
Goodman And Kruskal's Gamma
In statistics, Goodman and Kruskal's gamma is a measure of rank correlation, i.e., the similarity of the orderings of the data when ranked by each of the quantities. It measures the strength of association of the cross tabulated data when both variables are measured at the ordinal level. It makes no adjustment for either table size or ties. Values range from −1 (100% negative association, or perfect inversion) to +1 (100% positive association, or perfect agreement). A value of zero indicates the absence of association. This statistic (which is distinct from Goodman and Kruskal's lambda) is named after Leo Goodman and William Kruskal, who proposed it in a series of papers from 1954 to 1972. Definition The estimate of gamma, ''G'', depends on two quantities: :*''Ns'', the number of pairs of cases ranked in the same order on both variables (number of concordant pairs), :*''Nd'', the number of pairs of cases ranked in reversed order on both variables (number of reversed pai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kendall Rank Correlation Coefficient
In statistics, the Kendall rank correlation coefficient, commonly referred to as Kendall's τ coefficient (after the Greek letter τ, tau), is a statistic used to measure the ordinal association between two measured quantities. A τ test is a non-parametric hypothesis test for statistical dependence based on the τ coefficient. It is a measure of rank correlation: the similarity of the orderings of the data when ranked by each of the quantities. It is named after Maurice Kendall, who developed it in 1938, though Gustav Fechner had proposed a similar measure in the context of time series in 1897. Intuitively, the Kendall correlation between two variables will be high when observations have a similar (or identical for a correlation of 1) rank (i.e. relative position label of the observations within the variable: 1st, 2nd, 3rd, etc.) between the two variables, and low when observations have a dissimilar (or fully different for a correlation of −1) rank between the two variabl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Page's Trend Test
In statistics, the Page test for multiple comparisons between ordered correlated variables is the counterpart of Spearman's rank correlation coefficient which summarizes the association of continuous variables. It is also known as Page's trend test or Page's ''L'' test. It is a repeated measure trend test. The Page test is useful where: *there are three or more conditions, *a number of subjects (or other randomly sampled entities) are all observed in each of them, and *we predict that the observations will have a particular order. For example, a number of subjects might each be given three trials at the same task, and we predict that performance will improve from trial to trial. A test of the significance of the trend between conditions in this situation was developed by Ellis Batten Page (1963). More formally, the test considers the null hypothesis that, for ''n'' conditions, where ''m''''i'' is a measure of the central tendency of the ''i''th condition, :m_1 = m_2 = m_3 = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg)