|
Order-isomorphism
In the mathematical field of order theory, an order isomorphism is a special kind of monotone function that constitutes a suitable notion of isomorphism for partially ordered sets (posets). Whenever two posets are order isomorphic, they can be considered to be "essentially the same" in the sense that either of the orders can be obtained from the other just by renaming of elements. Two strictly weaker notions that relate to order isomorphisms are order embeddings and Galois connections. Definition Formally, given two posets (S,\le_S) and (T,\le_T), an order isomorphism from (S,\le_S) to (T,\le_T) is a bijective function f from S to T with the property that, for every x and y in S, x \le_S y if and only if f(x)\le_T f(y). That is, it is a bijective order-embedding. It is also possible to define an order isomorphism to be a surjective order-embedding. The two assumptions that f cover all the elements of T and that it preserve orderings, are enough to ensure that f is also one-to- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Order Theory
Order theory is a branch of mathematics that investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary. Background and motivation Orders are everywhere in mathematics and related fields like computer science. The first order often discussed in primary school is the standard order on the natural numbers e.g. "2 is less than 3", "10 is greater than 5", or "Does Tom have fewer cookies than Sally?". This intuitive concept can be extended to orders on other sets of numbers, such as the integers and the reals. The idea of being greater than or less than another number is one of the basic intuitions of number systems (compare with numeral systems) in general (although one usually is also interested in the actual differe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partially Ordered Set
In mathematics, especially order theory, a partially ordered set (also poset) formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation indicating that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering. The relation itself is called a "partial order." The word ''partial'' in the names "partial order" and "partially ordered set" is used as an indication that not every pair of elements needs to be comparable. That is, there may be pairs of elements for which neither element precedes the other in the poset. Partial orders thus generalize total orders, in which every pair is comparable. Informal definition A partial order defines a notion of comparison. Two elements ''x'' and ''y'' may stand in any of four mutually exclusive relationships to each other: either ''x'' ''y'', or ''x'' and ''y'' are ''inco ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Function
In mathematics, the inverse function of a function (also called the inverse of ) is a function that undoes the operation of . The inverse of exists if and only if is bijective, and if it exists, is denoted by f^ . For a function f\colon X\to Y, its inverse f^\colon Y\to X admits an explicit description: it sends each element y\in Y to the unique element x\in X such that . As an example, consider the real-valued function of a real variable given by . One can think of as the function which multiplies its input by 5 then subtracts 7 from the result. To undo this, one adds 7 to the input, then divides the result by 5. Therefore, the inverse of is the function f^\colon \R\to\R defined by f^(y) = \frac . Definitions Let be a function whose domain is the set , and whose codomain is the set . Then is ''invertible'' if there exists a function from to such that g(f(x))=x for all x\in X and f(g(y))=y for all y\in Y. If is invertible, then there is exactly one functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cantor's Isomorphism Theorem
In order theory and model theory, branches of mathematics, Cantor's isomorphism theorem states that every two countable dense unbounded linear orders are order-isomorphic. For instance, there is an isomorphism (a one-to-one order-preserving correspondence) between the numerical ordering of the rational numbers and the numerical ordering of the dyadic rationals, that can be described by Minkowski's question-mark function. The isomorphism theorem is named after Georg Cantor, who used it to characterize the (uncountable) ordering on the real numbers. It can be proved by a back-and-forth method that is also sometimes attributed to Cantor. The same back-and-forth method also proves that countable dense unbounded orders are highly symmetric, and can be applied to other kinds of structures. However, Cantor's original proof only used the "going forth" half of this method. In terms of model theory, the isomorphism theorem can be expressed by saying that the first-order theory of unbounde ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all rational numbers, also referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by boldface , or blackboard bold \mathbb. A rational number is a real number. The real numbers that are rational are those whose decimal expansion either terminates after a finite number of digits (example: ), or eventually begins to repeat the same finite sequence of digits over and over (example: ). This statement is true not only in base 10, but also in every other integer base, such as the binary and hexadecimal ones (see ). A real number that is not rational is called irrational. Irrational numbers include , , , and . Since the set of rational numbers is countable, and the set of real numbers is u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dyadic Rational
In mathematics, a dyadic rational or binary rational is a number that can be expressed as a fraction whose denominator is a power of two. For example, 1/2, 3/2, and 3/8 are dyadic rationals, but 1/3 is not. These numbers are important in computer science because they are the only ones with finite binary representations. Dyadic rationals also have applications in weights and measures, musical time signatures, and early mathematics education. They can accurately approximate any real number. The sum, difference, or product of any two dyadic rational numbers is another dyadic rational number, given by a simple formula. However, division of one dyadic rational number by another does not always produce a dyadic rational result. Mathematically, this means that the dyadic rational numbers form a ring, lying between the ring of integers and the field of rational numbers. This ring may be denoted \Z tfrac12/math>. In advanced mathematics, the dyadic rational numbers are central to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
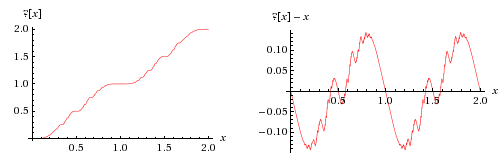
Minkowski's Question-mark Function
In mathematics, the Minkowski question-mark function, denoted , is a function with unusual fractal properties, defined by Hermann Minkowski in 1904. It maps quadratic irrational numbers to rational numbers on the unit interval, via an expression relating the continued fraction expansions of the quadratics to the binary expansions of the rationals, given by Arnaud Denjoy in 1938. It also maps rational numbers to dyadic rationals, as can be seen by a recursive definition closely related to the Stern–Brocot tree. Definition and intuition One way to define the question-mark function involves the correspondence between two different ways of representing fractional numbers using finite or infinite binary sequences. Most familiarly, a string of 0's and 1's with a single point mark ".", like "11.001001000011111..." can be interpreted as the binary representation of a number. In this case this number is 2+1+\frac18+\frac1+\cdots=\pi. There is a different way of interpreting the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Mathematical Analysis And Applications
The ''Journal of Mathematical Analysis and Applications'' is an academic journal in mathematics, specializing in mathematical analysis and related topics in applied mathematics. It was founded in 1960, as part of a series of new journals on areas of mathematics published by Academic Press, and is now published by Elsevier. For most years since 1997 it has been ranked by SCImago Journal Rank The SCImago Journal Rank (SJR) indicator is a measure of the prestige of scholarly journals that accounts for both the number of citations received by a journal and the prestige of the journals where the citations come from. Rationale Cita ... as among the top 50% of journals in its topic areas. retrieved 2017 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function Composition
In mathematics, function composition is an operation that takes two functions and , and produces a function such that . In this operation, the function is applied to the result of applying the function to . That is, the functions and are composed to yield a function that maps in domain to in codomain . Intuitively, if is a function of , and is a function of , then is a function of . The resulting ''composite'' function is denoted , defined by for all in . The notation is read as " of ", " after ", " circle ", " round ", " about ", " composed with ", " following ", " then ", or " on ", or "the composition of and ". Intuitively, composing functions is a chaining process in which the output of function feeds the input of function . The composition of functions is a special case of the composition of relations, sometimes also denoted by \circ. As a result, all properties of composition of relations are true of composition of functions, such as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed Interval
In mathematics, a (real) interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers satisfying is an interval which contains , , and all numbers in between. Other examples of intervals are the set of numbers such that , the set of all real numbers \R, the set of nonnegative real numbers, the set of positive real numbers, the empty set, and any singleton (set of one element). Real intervals play an important role in the theory of integration, because they are the simplest sets whose "length" (or "measure" or "size") is easy to define. The concept of measure can then be extended to more complicated sets of real numbers, leading to the Borel measure and eventually to the Lebesgue measure. Intervals are central to interval arithmetic, a general numerical computing technique that automatically provides guaranteed enclosures for arbitrary formulas, even in the presence of uncertainties, mathematica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |