|
Optical Pulses
In optics, an ultrashort pulse, also known as an ultrafast event, is an electromagnetic pulse whose time duration is of the order of a picosecond (10−12 second) or less. Such pulses have a broadband optical spectrum, and can be created by mode-locked oscillators. Amplification of ultrashort pulses almost always requires the technique of chirped pulse amplification, in order to avoid damage to the gain medium of the amplifier. They are characterized by a high peak intensity (or more correctly, irradiance) that usually leads to nonlinear interactions in various materials, including air. These processes are studied in the field of nonlinear optics. In the specialized literature, "ultrashort" refers to the femtosecond (fs) and picosecond (ps) range, although such pulses no longer hold the record for the shortest pulses artificially generated. Indeed, x-ray pulses with durations on the attosecond time scale have been reported. The 1999 Nobel Prize in Chemistry was awarded ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviolet, and infrared light. Because light is an electromagnetic wave, other forms of electromagnetic radiation such as X-rays, microwaves, and radio waves exhibit similar properties. Most optical phenomena can be accounted for by using the classical electromagnetic description of light. Complete electromagnetic descriptions of light are, however, often difficult to apply in practice. Practical optics is usually done using simplified models. The most common of these, geometric optics, treats light as a collection of rays that travel in straight lines and bend when they pass through or reflect from surfaces. Physical optics is a more comprehensive model of light, which includes wave effects such as diffraction and interference that cannot be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Packet
In physics, a wave packet (or wave train) is a short "burst" or "envelope" of localized wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere. Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet's profile may remain constant (no dispersion, see figure) or it may change (dispersion) while propagating. Quantum mechanics ascribes a special significance to the wave packet; it is interpreted as a probability amplitude, its norm squared describing the probability density that a particle or particles in a particular state will be measured to have a given position or momentum. The wave equation is in this case the Schrödinger equation, and through its ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uncertainty Principle
In quantum mechanics, the uncertainty principle (also known as Heisenberg's uncertainty principle) is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physical quantities of a particle, such as position, ''x'', and momentum, ''p'', can be predicted from initial conditions. Such variable pairs are known as complementary variables or canonically conjugate variables; and, depending on interpretation, the uncertainty principle limits to what extent such conjugate properties maintain their approximate meaning, as the mathematical framework of quantum physics does not support the notion of simultaneously well-defined conjugate properties expressed by a single value. The uncertainty principle implies that it is in general not possible to predict the value of a quantity with arbitrary certainty, even if all initial conditions are specified. Introduced first in 1927 by the German physicist Werner ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
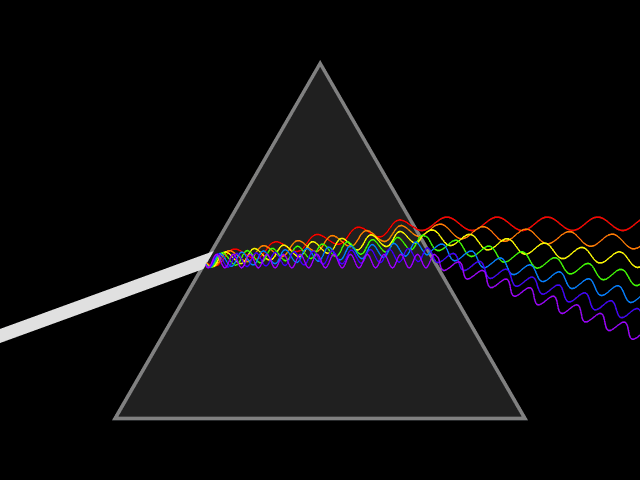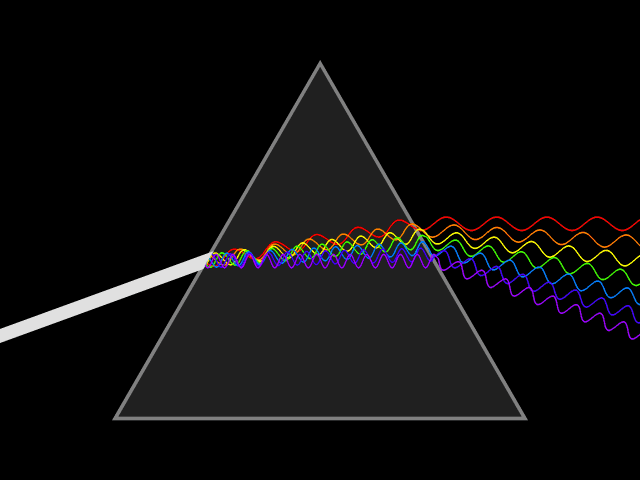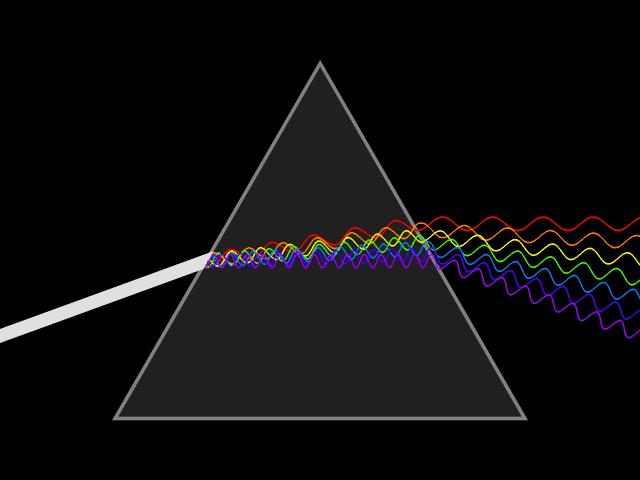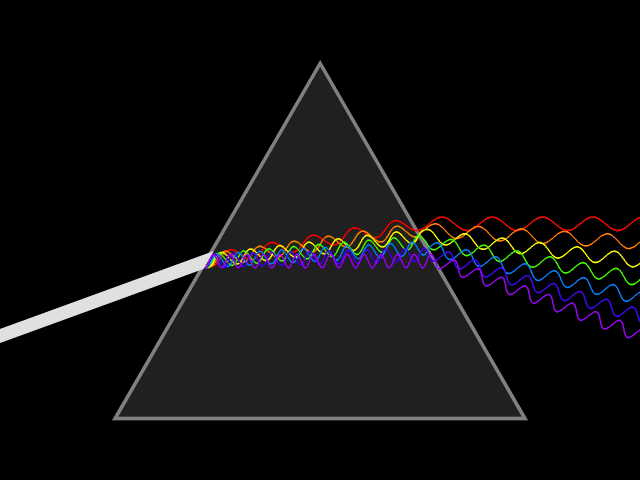
Dispersion (optics)
In optics, and by analogy other branches of physics dealing with wave propagation, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency; sometimes the term chromatic dispersion is used for specificity to optics in particular. A medium having this common property may be termed a dispersive medium (plural ''dispersive media''). Although the term is used in the field of optics to describe light and other electromagnetic waves, dispersion in the same sense can apply to any sort of wave motion such as acoustic dispersion in the case of sound and seismic waves, and in gravity waves (ocean waves). Within optics, dispersion is a property of telecommunication signals along transmission lines (such as microwaves in coaxial cable) or the pulses of light in optical fiber. Physically, dispersion translates in a loss of kinetic energy through absorption. In optics, one important and familiar consequence of dispersion is the change in the angle of refra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bandwidth-limited Pulse
A bandwidth-limited pulse (also known as Fourier-transform-limited pulse, or more commonly, transform-limited pulse) is a pulse of a wave that has the minimum possible duration for a given spectral bandwidth. Bandwidth-limited pulses have a constant phase across all frequencies making up the pulse. Optical pulses of this type can be generated by mode-locked lasers. Any waveform can be disassembled into its spectral components by Fourier analysis or Fourier transformation. The length of a pulse thereby is determined by its complex spectral components, which include not just their relative intensities, but also the relative positions (spectral phase) of these spectral components. For different pulse shapes, the minimum duration-bandwidth product is different. The duration-bandwidth product is minimal for zero phase-modulation. For example, \mathrm pulses have a minimum duration-bandwidth product of 0.315 while gaussian pulses have a minimum value of 0.441. A bandwidth-limited pul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Spectral Density
The power spectrum S_(f) of a time series x(t) describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of a certain signal or sort of signal (including noise) as analyzed in terms of its frequency content, is called its spectrum. When the energy of the signal is concentrated around a finite time interval, especially if its total energy is finite, one may compute the energy spectral density. More commonly used is the power spectral density (or simply power spectrum), which applies to signals existing over ''all'' time, or over a time period large enough (especially in relation to the duration of a measurement) that it could as well have been over an infinite time interval. The power spectral density (PSD) then refers to the spectral energy distribution that would be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Spectral Density
The power spectrum S_(f) of a time series x(t) describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of a certain signal or sort of signal (including noise) as analyzed in terms of its frequency content, is called its spectrum. When the energy of the signal is concentrated around a finite time interval, especially if its total energy is finite, one may compute the energy spectral density. More commonly used is the power spectral density (or simply power spectrum), which applies to signals existing over ''all'' time, or over a time period large enough (especially in relation to the duration of a measurement) that it could as well have been over an infinite time interval. The power spectral density (PSD) then refers to the spectral energy distribution that would be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, which will output a function depending on temporal frequency or spatial frequency respectively. That process is also called ''analysis''. An example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitches. The term ''Fourier transform'' refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time. The Fourier transform of a function is a complex-valued function representing the complex sinusoids that comprise the original function. For each frequency, the magnitude (absolute value) of the complex value represents the amplitude of a constituent complex sinusoid with that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytic Signal
In mathematics and signal processing, an analytic signal is a complex-valued function that has no negative frequency components. The real and imaginary parts of an analytic signal are real-valued functions related to each other by the Hilbert transform. The analytic representation of a real-valued function is an ''analytic signal'', comprising the original function and its Hilbert transform. This representation facilitates many mathematical manipulations. The basic idea is that the negative frequency components of the Fourier transform (or spectrum) of a real-valued function are superfluous, due to the Hermitian symmetry of such a spectrum. These negative frequency components can be discarded with no loss of information, provided one is willing to deal with a complex-valued function instead. That makes certain attributes of the function more accessible and facilitates the derivation of modulation and demodulation techniques, such as single-sideband. As long as the manipul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chirp
A chirp is a signal in which the frequency increases (''up-chirp'') or decreases (''down-chirp'') with time. In some sources, the term ''chirp'' is used interchangeably with sweep signal. It is commonly applied to sonar, radar, and laser systems, and to other applications, such as in spread-spectrum communications (see chirp spread spectrum). This signal type is biologically inspired and occurs as a phenomenon due to dispersion (a non-linear dependence between frequency and the propagation speed of the wave components). It is usually compensated for by using a matched filter, which can be part of the propagation channel. Depending on the specific performance measure, however, there are better techniques both for radar and communication. Since it was used in radar and space, it has been adopted also for communication standards. For automotive radar applications, it is usually called linear frequency modulated waveform (LFMW). In spread-spectrum usage, surface acoustic wave (SAW) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
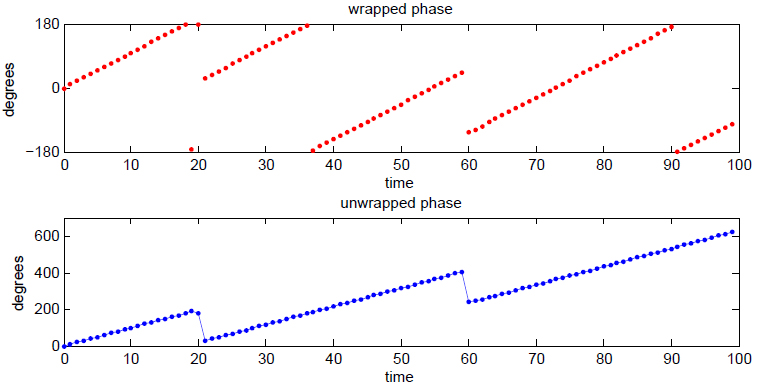
Instantaneous Phase
Instantaneous phase and frequency are important concepts in signal processing that occur in the context of the representation and analysis of time-varying functions. The instantaneous phase (also known as local phase or simply phase) of a ''complex-valued'' function ''s''(''t''), is the real-valued function: :\varphi(t) = \arg\, where arg is the complex argument function. The instantaneous frequency is the temporal rate of change of the instantaneous phase. And for a ''real-valued'' function ''s''(''t''), it is determined from the function's analytic representation, ''s''a(''t''): :\begin \varphi(t) &= \arg\ \\ pt &= \arg\, \end where \hat(t) represents the Hilbert transform of ''s''(''t''). When ''φ''(''t'') is constrained to its principal value, either the interval or , it is called ''wrapped phase''. Otherwise it is called ''unwrapped phase'', which is a continuous function of argument ''t'', assuming ''s''a(''t'') is a continuous function of ''t''. Unless ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Envelope (waves)
In physics and engineering, the envelope of an oscillating signal is a smooth curve outlining its extremes. The envelope thus generalizes the concept of a constant amplitude into an instantaneous amplitude. The figure illustrates a modulated sine wave varying between an ''upper envelope'' and a ''lower envelope''. The envelope function may be a function of time, space, angle, or indeed of any variable. In beating waves A common situation resulting in an envelope function in both space ''x'' and time ''t'' is the superposition of two waves of almost the same wavelength and frequency: : \begin F(x, \ t) & = \sin \left 2 \pi \left( \frac - ( f + \Delta f )t \right) \right+ \sin \left 2 \pi \left( \frac - ( f - \Delta f )t \right) \right\\ pt& \approx 2\cos \left 2 \pi \left( \frac - \Delta f \ t \right) \right\ \sin \left 2 \pi \left( \frac - f \ t \right) \right\end which uses the trigonometric formula for the addition of two sine waves, and the approximation&nbs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.gif)