|
Oblique Stereographic Projection
The stereographic projection, also known as the planisphere projection or the azimuthal conformal projection, is a conformal map projection whose use dates back to antiquity. Like the orthographic projection and gnomonic projection, the stereographic projection is an azimuthal projection, and when on a sphere, also a perspective projection. On an ellipsoid, the perspective definition of the stereographic projection is not conformal, and adjustments must be made to preserve its azimuthal and conformal properties. The universal polar stereographic coordinate system uses one such ellipsoidal implementation. History The stereographic projection was likely known in its polar aspect to the ancient Egyptians, though its invention is often credited to Hipparchus, who was the first Greek to use it. Its oblique aspect was used by Greek Mathematician Theon of Alexandria in the fourth century, and its equatorial aspect was used by Arab astronomer Al-Zarkali in the eleventh cent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stereographic Projection SW
Stereoscopy (also called stereoscopics, or stereo imaging) is a technique for creating or enhancing the illusion of depth in an image by means of stereopsis for binocular vision. The word ''stereoscopy'' derives . Any stereoscopic image is called a stereogram. Originally, stereogram referred to a pair of stereo images which could be viewed using a stereoscope. Most stereoscopic methods present a pair of two-dimensional images to the viewer. The left image is presented to the left eye and the right image is presented to the right eye. When viewed, the human brain perceives the images as a single 3D view, giving the viewer the perception of 3D depth. However, the 3D effect lacks proper focal depth, which gives rise to the Vergence-Accommodation Conflict. Stereoscopy is distinguished from other types of 3D displays that display an image in three full dimensions, allowing the observer to increase information about the 3-dimensional objects being displayed by head and eye move ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eastern Hemisphere
The Eastern Hemisphere is the half of the planet Earth which is east of the prime meridian (which crosses Greenwich, London, United Kingdom) and west of the antimeridian (which crosses the Pacific Ocean and relatively little land from pole to pole). It is also used to refer to Afro-Eurasia ( Africa and Eurasia) and Australia, in contrast with the Western Hemisphere, which includes mainly North and South America. The Eastern Hemisphere may also be called the "Oriental Hemisphere", and may in addition be used in a cultural or geopolitical sense as a synonym for the " Old World." Geography The almost perfect circle (the earth is an oblate that is fatter around the equator), drawn with a line, demarcating the Eastern and Western Hemispheres must be an arbitrarily decided and published convention, unlike the Equator (an imaginary line encircling Earth, equidistant from its poles), which divides the Northern and Southern Hemispheres. The prime meridian at 0° lon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gall Stereographic Projection
The Gall stereographic projection, presented by James Gall in 1855, is a cylindrical projection In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitu .... It is neither equal-area nor conformal but instead tries to balance the distortion inherent in any projection. Formulae The projection is conventionally defined as: :x = \frac\, ; \quad y = R \left(1+\frac\right)\tan \frac where ''λ'' is the longitude from the central meridian in degrees, ''φ'' is the latitude, and ''R'' is the radius of the globe used as the model of the earth for projection. It is a perspective projection if the point of projection is allowed to vary with longitude: the point of projection being on the equator on the opposite side of the earth from the point being mapped and with the projective surface being a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stereographic Projection In 3D
Stereoscopy (also called stereoscopics, or stereo imaging) is a technique for creating or enhancing the illusion of depth in an image by means of stereopsis for binocular vision. The word ''stereoscopy'' derives . Any stereoscopic image is called a stereogram. Originally, stereogram referred to a pair of stereo images which could be viewed using a stereoscope. Most stereoscopic methods present a pair of two-dimensional images to the viewer. The left image is presented to the left eye and the right image is presented to the right eye. When viewed, the human brain perceives the images as a single 3D view, giving the viewer the perception of 3D depth. However, the 3D effect lacks proper focal depth, which gives rise to the Vergence-Accommodation Conflict. Stereoscopy is distinguished from other types of 3D displays that display an image in three full dimensions, allowing the observer to increase information about the 3-dimensional objects being displayed by head and eye ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle Of A Sphere
A circle of a sphere is a circle that lies on a sphere. Such a circle can be formed as the intersection of a sphere and a plane, or of two spheres. Circles of a sphere are the spherical geometry analogs of generalised circles in Euclidean space. A circle on a sphere whose plane passes through the center of the sphere is called a ''great circle'', analogous to a Euclidean straight line; otherwise it is a small circle, analogous to a Euclidean circle. Circles of a sphere have radius less than or equal to the sphere radius, with equality when the circle is a great circle. A circle of a sphere can also be characterized as the locus of points on the sphere at uniform distance from a given center point, or as a spherical curve of constant curvature. On the earth In the geographic coordinate system on a globe, the parallels of latitude are small circles, with the Equator the only great circle. By contrast, all meridians of longitude, paired with their opposite meridian in the other ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point. Any arc of a great circle is a geodesic of the sphere, so that great circles in spherical geometry are the natural analog of straight lines in Euclidean space. For any pair of distinct non- antipodal points on the sphere, there is a unique great circle passing through both. (Every great circle through any point also passes through its antipodal point, so there are infinitely many great circles through two antipodal points.) The shorter of the two great-circle arcs between two distinct points on the sphere is called the ''minor arc'', and is the shortest surface-path between them. Its arc length is the great-circle distance between the points (the intrinsic distance on a sphere), and is proportional to the measure of the central angle formed by the two points and the center of the sphere. A great circle is the largest circle that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roussilhe Oblique Stereographic Projection
The Roussilhe oblique stereographic projection is a mapping projection developed by Henri Roussilhe in 1922. The projection uses a truncated series to approximate an oblique stereographic projection for the ellipsoid. The projection received some attention in the former Soviet Union.Snyder, John P. (1993). ''Flattening the Earth: Two Thousand Years of Map Projections'' p. 169. Chicago and London: The University of Chicago Press. . The development of the Bulgarian oblique stereographic projection was done for Romania by the Bulgarian geodesist, Hristow, in the late 1930s. See also *Map projection In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longit ... References External linkslibproj4 cartographic projection library with Roussilhe oblique stereographic projection support Map proje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conformal Latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or ''parallels'', run east–west as circles parallel to the equator. Latitude and ''longitude'' are used together as a coordinate pair to specify a location on the surface of the Earth. On its own, the term "latitude" normally refers to the ''geodetic latitude'' as defined below. Briefly, the geodetic latitude of a point is the angle formed between the vector perpendicular (or ''normal'') to the ellipsoidal surface from the point, and the plane of the equator. Background Two levels of abstraction are employed in the definitions of latitude and longitude. In the first step the physical surface is modeled by the geoid, a surface which approximates the mean sea level over the ocean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
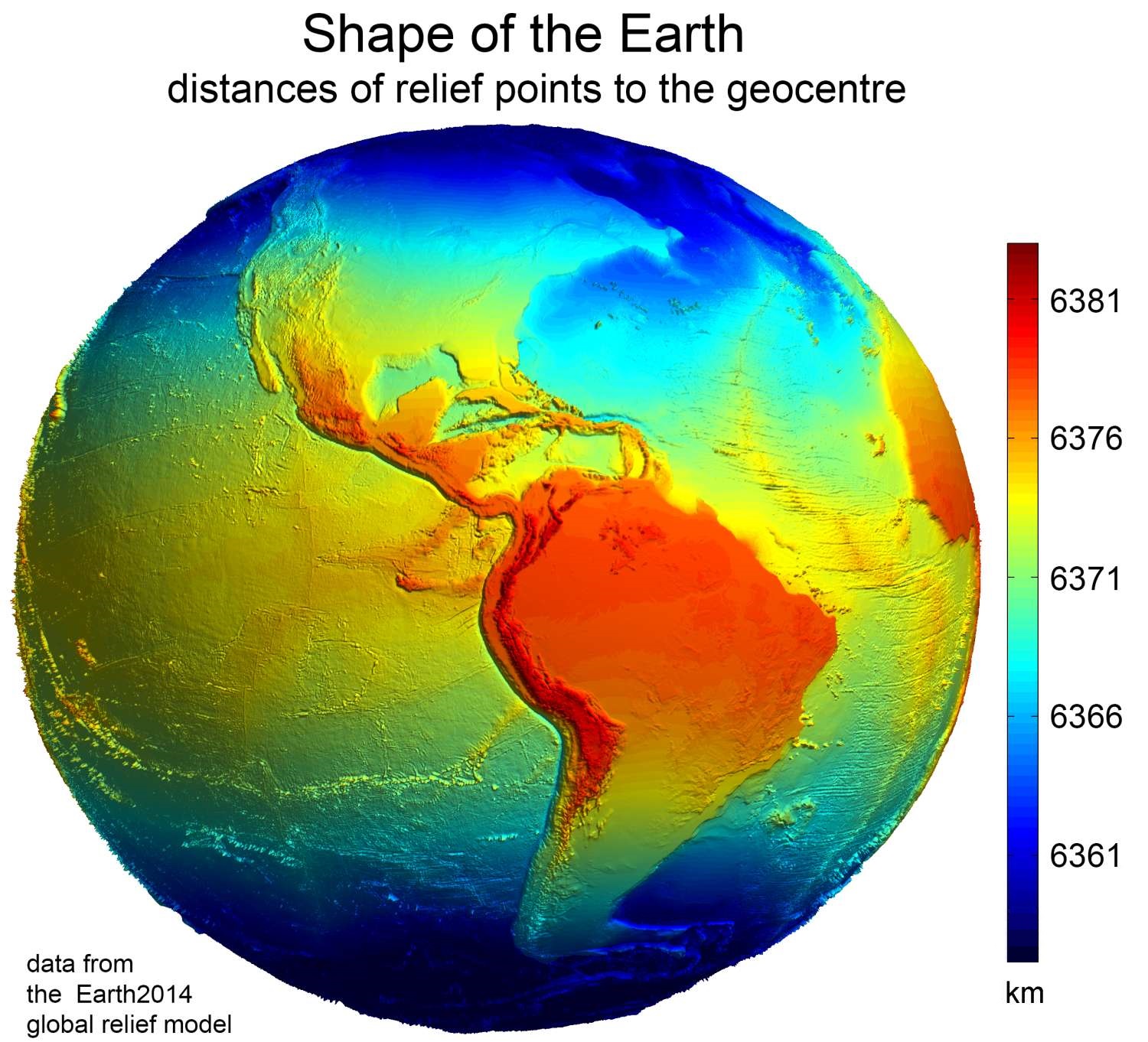
Figure Of The Earth
Figure of the Earth is a term of art in geodesy that refers to the size and shape used to model Earth. The size and shape it refers to depend on context, including the precision needed for the model. A sphere is a well-known historical approximation of the figure of the Earth that is satisfactory for many purposes. Several models with greater accuracy (including ellipsoid) have been developed so that coordinate systems can serve the precise needs of navigation, surveying, cadastre, land use, and various other concerns. Motivation Earth's topographic surface is apparent with its variety of land forms and water areas. This topographic surface is generally the concern of topographers, hydrographers, and geophysicists. While it is the surface on which Earth measurements are made, mathematically modeling it while taking the irregularities into account would be extremely complicated. The Pythagorean concept of a spherical Earth offers a simple surface that is easy to deal with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, theologian, and author (described in his time as a " natural philosopher"), widely recognised as one of the greatest mathematicians and physicists and among the most influential scientists of all time. He was a key figure in the philosophical revolution known as the Enlightenment. His book (''Mathematical Principles of Natural Philosophy''), first published in 1687, established classical mechanics. Newton also made seminal contributions to optics, and shares credit with German mathematician Gottfried Wilhelm Leibniz for developing infinitesimal calculus. In the , Newton formulated the laws of motion and universal gravitation that formed the dominant scientific viewpoint for centuries until it was superseded by the theory of relativity. Newton used his mathematical description of gravity to derive Kepler's laws of planetary motion, account for ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations. It has two major branches, differential calculus and integral calculus; the former concerns instantaneous rates of change, and the slopes of curves, while the latter concerns accumulation of quantities, and areas under or between curves. These two branches are related to each other by the fundamental theorem of calculus, and they make use of the fundamental notions of convergence of infinite sequences and infinite series to a well-defined limit. Infinitesimal calculus was developed independently in the late 17th century by Isaac Newton and Gottfried Wilhelm Leibniz. Later work, including codifying the idea of limits, put these developments on a more solid conceptual footing. Today, calculus has widespread uses in scienc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conformal Map
In mathematics, a conformal map is a function that locally preserves angles, but not necessarily lengths. More formally, let U and V be open subsets of \mathbb^n. A function f:U\to V is called conformal (or angle-preserving) at a point u_0\in U if it preserves angles between directed curves through u_0, as well as preserving orientation. Conformal maps preserve both angles and the shapes of infinitesimally small figures, but not necessarily their size or curvature. The conformal property may be described in terms of the Jacobian derivative matrix of a coordinate transformation. The transformation is conformal whenever the Jacobian at each point is a positive scalar times a rotation matrix (orthogonal with determinant one). Some authors define conformality to include orientation-reversing mappings whose Jacobians can be written as any scalar times any orthogonal matrix. For mappings in two dimensions, the (orientation-preserving) conformal mappings are precisely the locally ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |