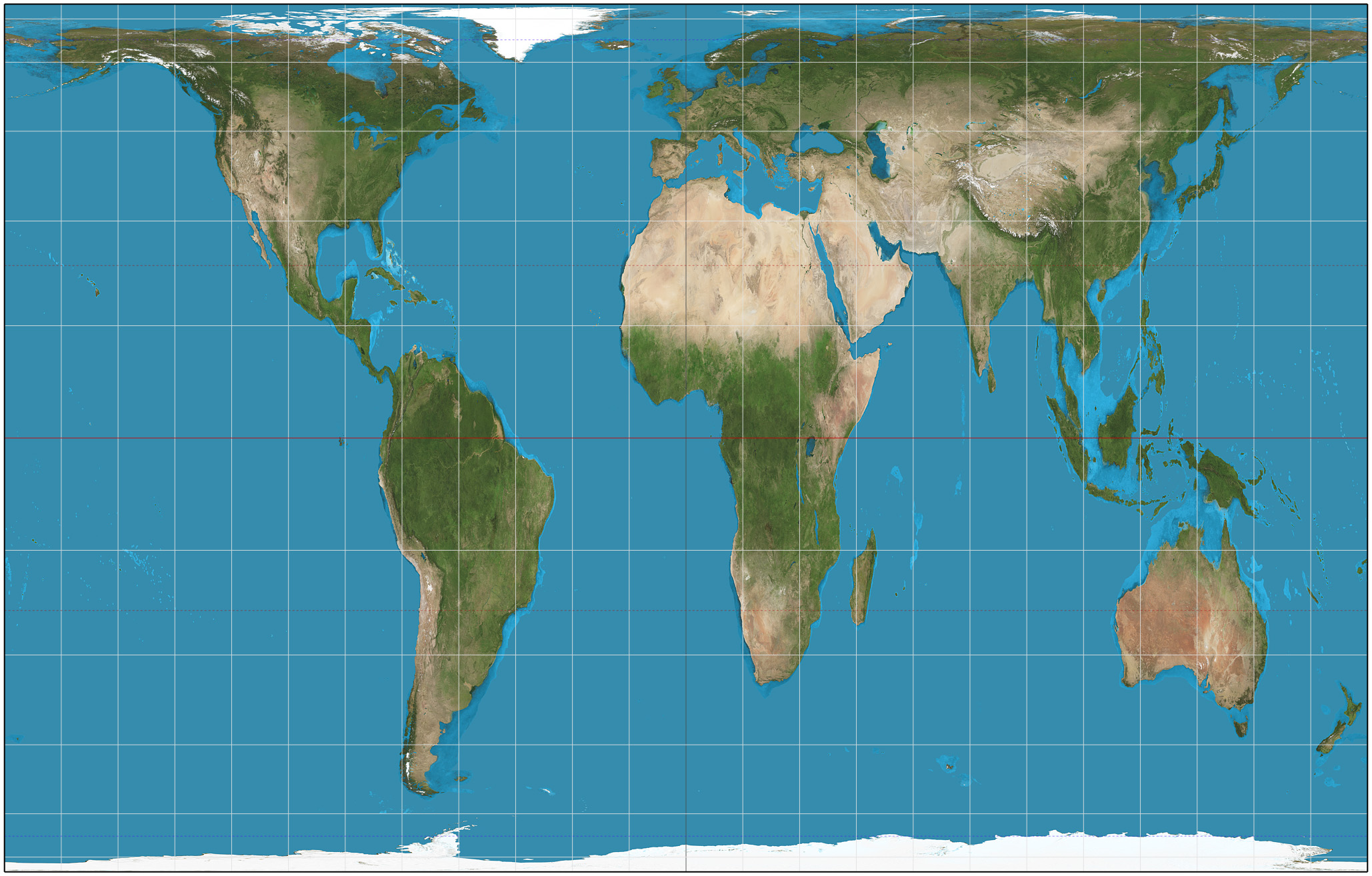
|
Gall Stereographic Projection
The Gall stereographic projection, presented by James Gall in 1855, is a cylindrical projection. It is neither equal-area nor conformal but instead tries to balance the distortion inherent in any projection. Formulae The projection is conventionally defined as: :x = \frac\, ; \quad y = R \left(1+\frac\right)\tan \frac where ''λ'' is the longitude from the central meridian in degrees, ''φ'' is the latitude, and ''R'' is the radius of the globe used as the model of the earth for projection. It is a perspective projection if the point of projection is allowed to vary with longitude: the point of projection being on the equator on the opposite side of the earth from the point being mapped and with the projective surface being a cylinder secant to the sphere at 45°N and 45°S. Gall called the projection "stereographic" because the spacing of the parallels is the same as the spacing of the parallels along the central meridian of the equatorial stereographic projection. The re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
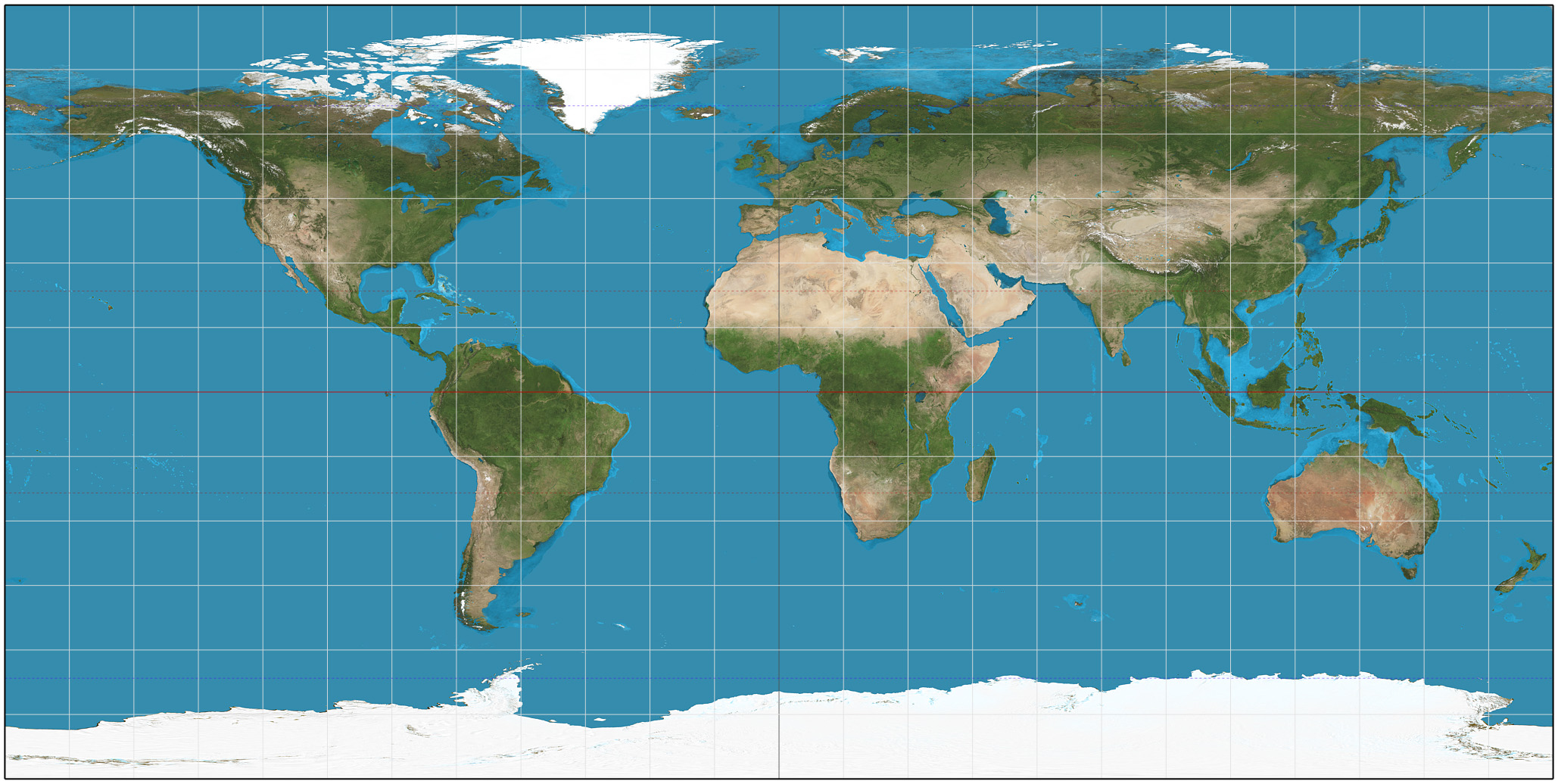
Gall Stereographic Projection SW Centered
Galls (from the Latin , 'oak-apple') or ''cecidia'' (from the Greek , anything gushing out) are a kind of swelling growth on the external Tissue (biology), tissues of plants, fungi, or animals. Plant galls are abnormal outgrowths of plant tissues, similar to benign tumors or warts in animals. They can be caused by various parasites, from viruses, fungi and bacteria, to other plants, insects and mites. Plant galls are often highly organized structures so that the cause of the gall can often be determined without the actual agent being identified. This applies particularly to some insect and mite plant galls. The study of plant galls is known as cecidology. In human pathology, a gall is a raised sore on the skin, usually caused by chafing or rubbing. Causes of plant galls Insects and mites Insect galls are the highly distinctive plant structures formed by some Herbivore, herbivorous insects as their own microhabitats. They are plant tissue which is controlled by the insect. Gal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gall Stereographic With Tissot's Indicatrices Of Distortion
Galls (from the Latin , 'oak-apple') or ''cecidia'' (from the Greek , anything gushing out) are a kind of swelling growth on the external tissues of plants, fungi, or animals. Plant galls are abnormal outgrowths of plant tissues, similar to benign tumors or warts in animals. They can be caused by various parasites, from viruses, fungi and bacteria, to other plants, insects and mites. Plant galls are often highly organized structures so that the cause of the gall can often be determined without the actual agent being identified. This applies particularly to some insect and mite plant galls. The study of plant galls is known as cecidology. In human pathology, a gall is a raised sore on the skin, usually caused by chafing or rubbing. Causes of plant galls Insects and mites Insect galls are the highly distinctive plant structures formed by some herbivorous insects as their own microhabitats. They are plant tissue which is controlled by the insect. Galls act as both the habitat a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James Gall
James Gall (27 September 1808 – 7 February 1895) was a Scottish clergyman who founded the Carrubbers Close Mission. He was also a cartographer, publisher, sculptor, astronomer and author. In cartography he gives his name to three different map projections: Gall stereographic; Gall isographic; and Gall orthographic (Gall–Peters projection). Life Gall was born on 27 September 1808, the son of Ann Collie and James Gall, a printer who founded the printing company of Gall & Inglis in Edinburgh, which specialised in easy-access astronomy. His uncle, John Gall, ran a coach-building business. He was baptised at St Cuthbert's Church, Edinburgh on 15 October 1808.He lived with his family at Potterrow on the South Side of Edinburgh. He was educated at the High School close to his home and at the Trustees Academy. He was then apprenticed as a printer in his father's firm from 1822 before studying at the University of Edinburgh. From 1838 he became a partner in his father's pu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Map Projection
In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way and to some extent. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, projections are considered in several fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle Of Latitude
A circle of latitude or line of latitude on Earth is an abstract east–west small circle connecting all locations around Earth (ignoring elevation) at a given latitude coordinate line. Circles of latitude are often called parallels because they are Parallel (geometry), parallel to each other; that is, planes that contain any of these circles never Intersection, intersect each other. A location's position along a circle of latitude is given by its longitude. Circles of latitude are unlike circles of longitude, which are all great circles with the centre of Earth in the middle, as the circles of latitude get smaller as the distance from the Equator increases. Their length can be calculated by a common sine or cosine function. The 60th parallel north or 60th parallel south, south is half as long as the Equator (disregarding Earth's minor flattening by 0.335%). On the Mercator projection or on the Gall-Peters projection, a circle of latitude is perpendicular to all meridian (geo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meridian (geography)
In geography and geodesy, a meridian is the locus connecting points of equal longitude, which is the angle (in degrees or other units) east or west of a given prime meridian (currently, the IERS Reference Meridian). In other words, it is a line of longitude. The position of a point along the meridian is given by that longitude and its latitude, measured in angular degrees north or south of the Equator. On a Mercator projection or on a Gall-Peters projection, each meridian is perpendicular to all circles of latitude. A meridian is half of a great circle on Earth's surface. The length of a meridian on a modern ellipsoid model of Earth (WGS 84) has been estimated as . Pre-Greenwich The first prime meridian was set by Eratosthenes in 200 BCE. This prime meridian was used to provide measurement of the earth, but had many problems because of the lack of latitude measurement. Many years later around the 19th century there were still concerns of the prime meridian. Multiple loc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
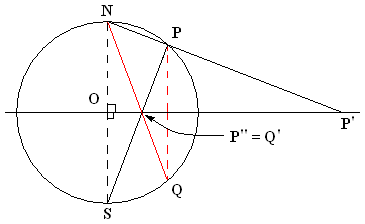
Stereographic Projection
In mathematics, a stereographic projection is a perspective projection of the sphere, through a specific point on the sphere (the ''pole'' or ''center of projection''), onto a plane (geometry), plane (the ''projection plane'') perpendicular to the diameter through the point. It is a smooth function, smooth, bijection, bijective function (mathematics), function from the entire sphere except the center of projection to the entire plane. It maps circle of a sphere, circles on the sphere to generalised circle, circles or lines on the plane, and is conformal map, conformal, meaning that it preserves angles at which curves meet and thus Local property, locally approximately preserves similarity (geometry), shapes. It is neither isometry, isometric (distance preserving) nor Equiareal map, equiareal (area preserving). The stereographic projection gives a way to representation (mathematics), represent a sphere by a plane. The metric tensor, metric induced metric, induced by the inverse s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Map Projections
This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise notable Notability is the property of being worthy of notice, having fame, or being considered to be of a high degree of interest, significance, or distinction. It also refers to the capacity to be such. Persons who are notable due to public responsibi .... Because there is no limit to the number of possible map projections, there can be no comprehensive list. Table of projections *The first known popularizer/user and not necessarily the creator. Key Type of projection ; Cylindrical: In standard presentation, these map regularly-spaced meridians to equally spaced vertical lines, and parallels to horizontal lines. ; Pseudocylindrical: In standard presentation, these map the central meridian and parallels as straight lines. Other meridians are curves (or possibly straight from pole to equator), regularly spaced along parallels. ; Conic: In standard presentation, conic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Map Projections
In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way and to some extent. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, projections are considered in several fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
