|
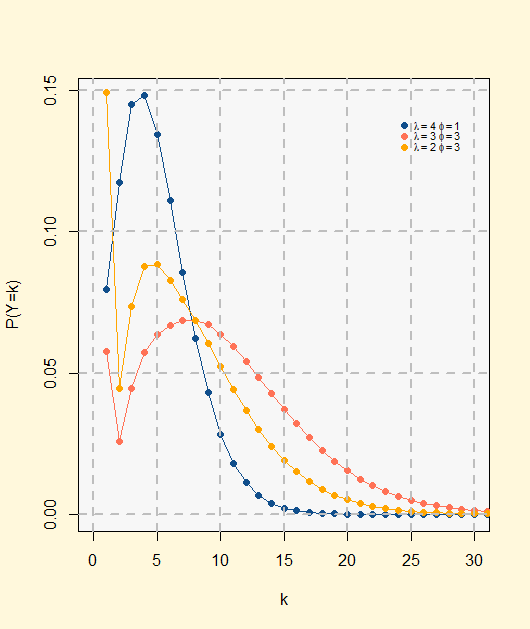
Neyman Type A Distribution
In statistics and probability, the Neyman Type A distribution is a discrete probability distribution from the family of Compound Poisson distribution. First of all, to easily understand this distribution we will demonstrate it with the following example explained in Univariate Discret Distributions; we have a statistical model of the distribution of larvae in a unit area of field (in a unit of habitat) by assuming that the variation in the number of clusters of eggs per unit area (per unit of habitat) could be represented by a Poisson distribution with parameter \lambda , while the number of larvae developing per cluster of eggs are assumed to have independent Poisson distribution all with the same parameter \phi . If we want to know how many larvae there are, we define a random variable ''Y'' as the sum of the number of larvae hatched in each group (given ''j'' groups). Therefore, ''Y'' = ''X''1 + ''X''2 + ... ''X'' j, where ''X''1,...,''X''j are independent Poisson variables w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stirling Numbers Of The Second Kind
In mathematics, particularly in combinatorics, a Stirling number of the second kind (or Stirling partition number) is the number of ways to partition a set of ''n'' objects into ''k'' non-empty subsets and is denoted by S(n,k) or \textstyle \left\. Stirling numbers of the second kind occur in the field of mathematics called combinatorics and the study of partitions. They are named after James Stirling. The Stirling numbers of the first and second kind can be understood as inverses of one another when viewed as triangular matrices. This article is devoted to specifics of Stirling numbers of the second kind. Identities linking the two kinds appear in the article on Stirling numbers. Definition The Stirling numbers of the second kind, written S(n,k) or \lbrace\textstyle\rbrace or with other notations, count the number of ways to partition a set of n labelled objects into k nonempty unlabelled subsets. Equivalently, they count the number of different equivalence relations wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean, mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would expect to get in reality. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by Integral, integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characteristic Function
In mathematics, the term "characteristic function" can refer to any of several distinct concepts: * The indicator function of a subset, that is the function \mathbf_A\colon X \to \, which for a given subset ''A'' of ''X'', has value 1 at points of ''A'' and 0 at points of ''X'' − ''A''. * The characteristic function in convex analysis, closely related to the indicator function of a set: \chi_A (x) := \begin 0, & x \in A; \\ + \infty, & x \not \in A. \end * In probability theory, the characteristic function of any probability distribution on the real line is given by the following formula, where ''X'' is any random variable with the distribution in question: \varphi_X(t) = \operatorname\left(e^\right), where \operatorname denotes expected value. For multivariate distributions, the product ''tX'' is replaced by a scalar product of vectors. * The characteristic function of a cooperative game in game theory. * The characteristic polynomial in linear algebra. * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Distribution
In probability theory and statistics, a probability distribution is a function that gives the probabilities of occurrence of possible events for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The sa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is f(x) = \frac e^\,. The parameter is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma^2 is the variance. The standard deviation of the distribution is (sigma). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Excess Kurtosis
In probability theory and statistics, kurtosis (from , ''kyrtos'' or ''kurtos'', meaning "curved, arching") refers to the degree of “tailedness” in the probability distribution of a real-valued random variable. Similar to skewness, kurtosis provides insight into specific characteristics of a distribution. Various methods exist for quantifying kurtosis in theoretical distributions, and corresponding techniques allow estimation based on sample data from a population. It’s important to note that different measures of kurtosis can yield varying interpretations. The standard measure of a distribution's kurtosis, originating with Karl Pearson, is a scaled version of the fourth moment of the distribution. This number is related to the tails of the distribution, not its peak; hence, the sometimes-seen characterization of kurtosis as " peakedness" is incorrect. For this measure, higher kurtosis corresponds to greater extremity of deviations (or outliers), and not the configurat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for example, the variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical applications is that, unlike the standard deviation, its units differ from the random variable, which is why the standard devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kurtosis
In probability theory and statistics, kurtosis (from , ''kyrtos'' or ''kurtos'', meaning "curved, arching") refers to the degree of “tailedness” in the probability distribution of a real-valued random variable. Similar to skewness, kurtosis provides insight into specific characteristics of a distribution. Various methods exist for quantifying kurtosis in theoretical distributions, and corresponding techniques allow estimation based on sample data from a population. It’s important to note that different measures of kurtosis can yield varying interpretations. The standard measure of a distribution's kurtosis, originating with Karl Pearson, is a scaled version of the fourth moment of the distribution. This number is related to the tails of the distribution, not its peak; hence, the sometimes-seen characterization of kurtosis as " peakedness" is incorrect. For this measure, higher kurtosis corresponds to greater extremity of deviations (or outliers), and not the configur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Deviation
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its Expected value, mean. A low standard Deviation (statistics), deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range. The standard deviation is commonly used in the determination of what constitutes an outlier and what does not. Standard deviation may be abbreviated SD or std dev, and is most commonly represented in mathematical texts and equations by the lowercase Greek alphabet, Greek letter Sigma, σ (sigma), for the population standard deviation, or the Latin script, Latin letter ''s'', for the sample standard deviation. The standard deviation of a random variable, Sample (statistics), sample, statistical population, data set, or probability distribution is the square root of its variance. (For a finite population, v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statistics. Each attempts to summarize or typify a given group of data, illustrating the magnitude and sign of the data set. Which of these measures is most illuminating depends on what is being measured, and on context and purpose. The ''arithmetic mean'', also known as "arithmetic average", is the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the numbers are from observing a sample of a larger group, the arithmetic mean is termed the '' sample mean'' (\bar) to distinguish it from the group mean (or expected value) of the underlying distribution, denoted \mu or \mu_x. Outside probability and statistics, a wide rang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined. For a unimodal distribution (a distribution with a single peak), negative skew commonly indicates that the ''tail'' is on the left side of the distribution, and positive skew indicates that the tail is on the right. In cases where one tail is long but the other tail is fat, skewness does not obey a simple rule. For example, a zero value in skewness means that the tails on both sides of the mean balance out overall; this is the case for a symmetric distribution but can also be true for an asymmetric distribution where one tail is long and thin, and the other is short but fat. Thus, the judgement on the symmetry of a given distribution by using only its skewness is risky; the distribution shape must be taken into account. Introduction Consider the two d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |