|
Newman–Janis Algorithm
In general relativity, the Newman–Janis algorithm (NJA) is a complexification technique for finding exact solutions to the Einstein field equations. In 1964, Newman and Janis showed that the Kerr metric could be obtained from the Schwarzschild metric by means of a coordinate transformation and allowing the radial coordinate to take on complex values. Originally, no clear reason for why the algorithm works was known. In 1998, Drake and Szekeres gave a detailed explanation of the success of the algorithm and proved the uniqueness of certain solutions. In particular, the only perfect fluid solution generated by NJA is the Kerr metric and the only Petrov type D solution is the Kerr–Newman metric The Kerr–Newman metric is the most general asymptotically flat, stationary solution of the Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding an electrically charged, rotating ma .... The algorithm works well on ''ƒ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the ' is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations. Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complexification
In mathematics, the complexification of a vector space over the field of real numbers (a "real vector space") yields a vector space over the complex number field, obtained by formally extending the scaling of vectors by real numbers to include their scaling ("multiplication") by complex numbers. Any basis for (a space over the real numbers) may also serve as a basis for over the complex numbers. Formal definition Let V be a real vector space. The of is defined by taking the tensor product of V with the complex numbers (thought of as a 2-dimensional vector space over the reals): :V^ = V\otimes_ \Complex\,. The subscript, \R, on the tensor product indicates that the tensor product is taken over the real numbers (since V is a real vector space this is the only sensible option anyway, so the subscript can safely be omitted). As it stands, V^ is only a real vector space. However, we can make V^ into a complex vector space by defining complex multiplication as follows: :\alpha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exact Solutions In General Relativity
In general relativity, an exact solution is a solution of the Einstein field equations whose derivation does not invoke simplifying assumptions, though the starting point for that derivation may be an idealized case like a perfectly spherical shape of matter. Mathematically, finding an exact solution means finding a Lorentzian manifold equipped with tensor fields modeling states of ordinary matter, such as a fluid, or classical non-gravitational fields such as the electromagnetic field. Background and definition These tensor fields should obey any relevant physical laws (for example, any electromagnetic field must satisfy Maxwell's equations). Following a standard recipe which is widely used in mathematical physics, these tensor fields should also give rise to specific contributions to the stress–energy tensor T^. (A field is described by a Lagrangian, varying with respect to the field should give the field equations and varying with respect to the metric should give the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstein Field Equations
In the general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of matter within it. The equations were published by Einstein in 1915 in the form of a tensor equation which related the local ' (expressed by the Einstein tensor) with the local energy, momentum and stress within that spacetime (expressed by the stress–energy tensor). Analogously to the way that electromagnetic fields are related to the distribution of charges and currents via Maxwell's equations, the EFE relate the spacetime geometry to the distribution of mass–energy, momentum and stress, that is, they determine the metric tensor of spacetime for a given arrangement of stress–energy–momentum in the spacetime. The relationship between the metric tensor and the Einstein tensor allows the EFE to be written as a set of nonlinear partial differential equations when used in this way. The solutions of the EF ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
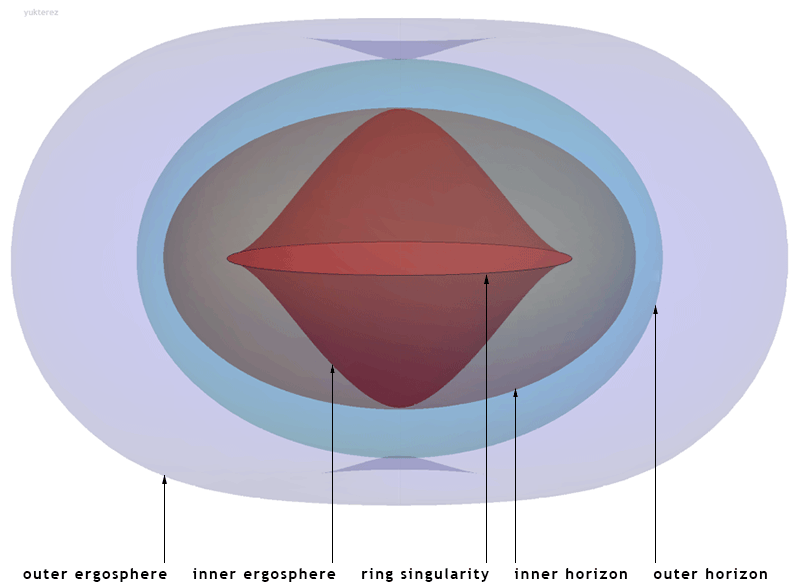
Kerr Metric
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find. Overview The Kerr metric is a generalization to a rotating body of the Schwarzschild metric, discovered by Karl Schwarzschild in 1915, which described the geometry of spacetime around an uncharged, spherically symmetric, and non-rotating body. The corresponding solution for a ''charged'', spherical, non-rotating body, the Reissner–Nordström metric, was discovered soon afterwards (1916–1918). However, the exact solution for an uncharged, ''rotating'' black hole, the Kerr metric, remained unsolved until 1963, when it was discovered by Roy Kerr.Melia, Fulvio (2009). "Cracking the Einstein code: relativity and the birth of b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schwarzschild Metric
In Einstein's theory of general relativity, the Schwarzschild metric (also known as the Schwarzschild solution) is an exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, angular momentum of the mass, and universal cosmological constant are all zero. The solution is a useful approximation for describing slowly rotating astronomical objects such as many stars and planets, including Earth and the Sun. It was found by Karl Schwarzschild in 1916, and around the same time independently by Johannes Droste, who published his more complete and modern-looking discussion four months after Schwarzschild. According to Birkhoff's theorem, the Schwarzschild metric is the most general spherically symmetric vacuum solution of the Einstein field equations. A Schwarzschild black hole or static black hole is a black hole that has neither electric charge nor angular momentum. A Sch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Petrov Type
In differential geometry and theoretical physics, the Petrov classification (also known as Petrov–Pirani–Penrose classification) describes the possible algebraic symmetries of the Weyl tensor at each event in a Lorentzian manifold. It is most often applied in studying exact solutions of Einstein's field equations, but strictly speaking the classification is a theorem in pure mathematics applying to any Lorentzian manifold, independent of any physical interpretation. The classification was found in 1954 by A. Z. Petrov and independently by Felix Pirani in 1957. Classification theorem We can think of a fourth rank tensor such as the Weyl tensor, ''evaluated at some event'', as acting on the space of bivectors at that event like a linear operator acting on a vector space: : X^ \rightarrow \frac \, _ X^ Then, it is natural to consider the problem of finding eigenvalues \lambda and eigenvectors (which are now referred to as eigenbivectors) X^ such that :\frac \, _ \, X^ = \lam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kerr–Newman Metric
The Kerr–Newman metric is the most general asymptotically flat, stationary solution of the Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding an electrically charged, rotating mass. It generalizes the Kerr metric by taking into account the field energy of an electromagnetic field, in addition to describing rotation. It is one of a large number of various different electrovacuum solutions, that is, of solutions to the Einstein–Maxwell equations which account for the field energy of an electromagnetic field. Such solutions do not include any electric charges other than that associated with the gravitational field, and are thus termed vacuum solutions. This solution has not been especially useful for describing astrophysical phenomena, because observed astronomical objects do not possess an appreciable net electric charge, and the magnetic fields of stars arise through other processes. As a model of realistic black ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brane Cosmology
Brane cosmology refers to several theories in particle physics and cosmology related to string theory, superstring theory and M-theory. Brane and bulk The central idea is that the visible, three-dimensional universe is restricted to a brane inside a higher-dimensional space, called the "bulk" (also known as "hyperspace"). If the additional dimensions are compact, then the observed universe contains the extra dimension, and then no reference to the bulk is appropriate. In the bulk model, at least some of the extra dimensions are extensive (possibly infinite), and other branes may be moving through this bulk. Interactions with the bulk, and possibly with other branes, can influence our brane and thus introduce effects not seen in more standard cosmological models. Why gravity is weak and the cosmological constant is small Some versions of brane cosmology, based on the large extra dimension idea, can explain the weakness of gravity relative to the other fundamental forces of natu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Born–Infeld Model
In theoretical physics, the Born–Infeld model is a particular example of what is usually known as a nonlinear electrodynamics. It was historically introduced in the 1930s to remove the divergence of the electron's self-energy in classical electrodynamics by introducing an upper bound of the electric field at the origin. Overview Born–Infeld electrodynamics is named after physicists Max Born and Leopold Infeld, who first proposed it. The model possesses a whole series of physically interesting properties. In analogy to a relativistic limit on velocity, Born–Infeld theory proposes a limiting force via limited electric field strength. A maximum electric field strength produces a finite electric field self-energy, which when attributed entirely to electron mass-produces maximum field :E_ = 1.187 \times 10^ \, \mathrm / \mathrm. Born–Infeld electrodynamics displays good physical properties concerning wave propagation, such as the absence of shock waves and birefringence. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Birkhoff's Theorem (relativity)
In general relativity, Birkhoff's theorem states that any spherically symmetric solution of the vacuum field equations must be static and asymptotically flat. This means that the exterior solution (i.e. the spacetime outside of a spherical, nonrotating, gravitating body) must be given by the Schwarzschild metric. The converse of the theorem is true and is called Israel's theorem. The converse is not true in Newtonian gravity. The theorem was proven in 1923 by George David Birkhoff (author of another famous '' Birkhoff theorem'', the ''pointwise ergodic theorem'' which lies at the foundation of ergodic theory). However, Nils Voje Johansen, Finn Ravndal, Stanley Deser recently pointed out that it was published two years earlier by a little-known Norwegian physicist, Jørg Tofte Jebsen.J.T. Jebsen, ''Uber die allgemeinen kugelsymmetrischen Lösungen der Einsteinschen Gravitationsgleichungen im Vakuum'', Arkiv för matematik, astronomi och fysik, 15 (18), 1 - 9 (1921).J.T. Jebse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithms
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can perform automated deductions (referred to as automated reasoning) and use mathematical and logical tests to divert the code execution through various routes (referred to as automated decision-making). Using human characteristics as descriptors of machines in metaphorical ways was already practiced by Alan Turing with terms such as "memory", "search" and "stimulus". In contrast, a heuristic is an approach to problem solving that may not be fully specified or may not guarantee correct or optimal results, especially in problem domains where there is no well-defined correct or optimal result. As an effective method, an algorithm can be expressed within a finite amount of space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |