|
N. Mukunda
Narasimhaiengar Mukunda (born 25 January 1939, New Delhi, India) is an Indian theoretical physicist. Mukunda's higher education began at Delhi University, where he was granted a B.Sc. (Hon) degree in 1953. For his Ph.D. he studied at University of Rochester with E. C. G. Sudarshan and graduated in 1964. Mukunda’s thesis dealt with Hamiltonian mechanics, symmetry groups and elementary particles. He also studied group theory at Princeton University with Valentine Bargmann, including topological groups and Lie theory. He was a post-doctoral fellow at Syracuse University before he returned to India. In 1967, he became a Fellow at Tata Institute of Fundamental Research. In 1969 he transferred to IISc, Bangalore. From 1972 to 2001 he served as professor at the Center for Theoretical Studies. Using the notes from Bargmann's lectures, Mukunda contributed chapters on Lie groups to ''Classical Dynamics: a modern perspective'' that he authored with Sudarshan in 1974. The expression o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
New Delhi
New Delhi (, , ''Naī Dillī'') is the capital of India and a part of the National Capital Territory of Delhi (NCT). New Delhi is the seat of all three branches of the government of India, hosting the Rashtrapati Bhavan, Parliament House, and the Supreme Court of India. New Delhi is a municipality within the NCT, administered by the NDMC, which covers mostly Lutyens' Delhi and a few adjacent areas. The municipal area is part of a larger administrative district, the New Delhi district. Although colloquially ''Delhi'' and ''New Delhi'' are used interchangeably to refer to the National Capital Territory of Delhi, both are distinct entities, with both the municipality and the New Delhi district forming a relatively small part of the megacity of Delhi. The National Capital Region is a much larger entity comprising the entire NCT along with adjoining districts in neighbouring states, including Ghaziabad, Noida, Gurgaon and Faridabad. The foundation stone of New De ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classical Group
In mathematics, the classical groups are defined as the special linear groups over the reals , the complex numbers and the quaternions together with special automorphism groups of symmetric or skew-symmetric bilinear forms and Hermitian or skew-Hermitian sesquilinear forms defined on real, complex and quaternionic finite-dimensional vector spaces. Of these, the complex classical Lie groups are four infinite families of Lie groups that together with the exceptional groups exhaust the classification of simple Lie groups. The compact classical groups are compact real forms of the complex classical groups. The finite analogues of the classical groups are the classical groups of Lie type. The term "classical group" was coined by Hermann Weyl, it being the title of his 1939 monograph '' The Classical Groups''. The classical groups form the deepest and most useful part of the subject of linear Lie groups. Most types of classical groups find application in classical and modern phys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Reviews
''Mathematical Reviews'' is a journal published by the American Mathematical Society (AMS) that contains brief synopses, and in some cases evaluations, of many articles in mathematics, statistics, and theoretical computer science. The AMS also publishes an associated online bibliographic database called MathSciNet which contains an electronic version of ''Mathematical Reviews'' and additionally contains citation information for over 3.5 million items as of 2018. Reviews Mathematical Reviews was founded by Otto E. Neugebauer in 1940 as an alternative to the German journal ''Zentralblatt für Mathematik'', which Neugebauer had also founded a decade earlier, but which under the Nazis had begun censoring reviews by and of Jewish mathematicians. The goal of the new journal was to give reviews of every mathematical research publication. As of November 2007, the ''Mathematical Reviews'' database contained information on over 2.2 million articles. The authors of reviews are volunteer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ramakrishna Mission Vivekananda Educational And Research Institute
Ramakrishna Mission Vivekananda Educational and Research Institute, formerly Ramakrishna Mission Vivekananda University or simply Vivekananda University, is a education institute deemed-to-be-university headquartered at Belur, West Bengal, with campuses spanning multiple states in India. Established with the idea of actualizing Swami Vivekananda's vision of education, the institute is administered by the Ramakrishna Mission. The university provides courses on subjects as varied as rural and tribal development, disability management and special education, fundamental science education and Indian cultural and spiritual heritage. History Ramakrishna Mission Vivekananda Educational and Research Institute was established with the idea of actualizing Swami Vivekananda's vision of education. It was declared as a de novo Deemed University by the Ministry of Human Resource Development, Government of India in 2005. With its headquarters at Belur, RKMVERI began functioning in July 2 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
IISER Thiruvananthapuram
Indian Institute of Science Education and Research, Thiruvananthapuram (abbreviated as IISER Thiruvananthapuram or IISER-TVM) is an autonomous public university located in Thiruvananthapuram, India. The institute is one of the seven IISERs established by the Ministry of Human Resource Development, Government of India, to bridge the gap between research and basic sciences' education at the undergraduate level. The six other IISERs are IISER Bhopal, IISER Kolkata, IISER Mohali, IISER Pune, IISER Tirupati and IISER Berhampur. All IISERs were declared as Institutes of National Importance by the Parliament of India in 2012 through the NIT Amendment Act. IISER Thiruvananthapuram is an autonomous institution that awards Bachelor of Science & Master of Science (BS-MS) dual-degrees, and Doctor of Philosophy (Ph.D.) degrees in Mathematics, Physics, Chemistry and Biology. IISER TVM is to offer five new BS-MS programmes (i2 Sciences) and new 2 year M.Sc programmes in 2021. The campus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
IISER Mohali
Indian Institute of Science Education and Research, Mohali (IISER Mohali) is an autonomous public university established in 2006 at Mohali, Punjab, India. It is one of the seven Indian Institutes of Science Education and Research (IISERs), established by the Ministry of Human Resources and Development, Government of India, to research in frontier areas of science and to provide science education at the undergraduate and postgraduate level. It was established after IISER Pune and IISER Kolkata and is recognised as an Institute of National Importance by the Government of India. It promote research in various fields of science. History The institute was approved by The Planning Commission in New Delhi in July 2006 and land was provided by The Punjab State government. The foundation stone of IISER Mohali was laid on 27 September 2006 by the former Prime Minister of India, Manmohan Singh. The Computing Facility of IISER Mohali was inaugurated on 3 September 2007 by T. Ramasami (Sec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
IISER Bhopal
Indian Institute of Science Education and Research, Bhopal (IISER-B or IISER – Bhopal) is an autonomous institute. ] in Bhauri, Bhopal district, Madhya Pradesh, India. It was established by the Ministry of Human Resource Development, Government of India in 2008 in order to incorporate research in basic science at undergraduate and graduate level, with equal emphasis on higher education for research and education in science. It is an autonomous institution awarding its own degrees. History Indian Institutes of Science Education and Research (IISERs) were created in 2006 through a proclamation of Ministry of Human Resource Development, Government of India, under the category of institutes of national importance, to promote quality education and research in basic sciences. Soon after the announcement, two of these institutes at Pune and Kolkata, respectively, were started in 2006. This was followed by institutes at Mohali (2007), Bhopal and Thiruvananthapuram (2008), Tirupa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
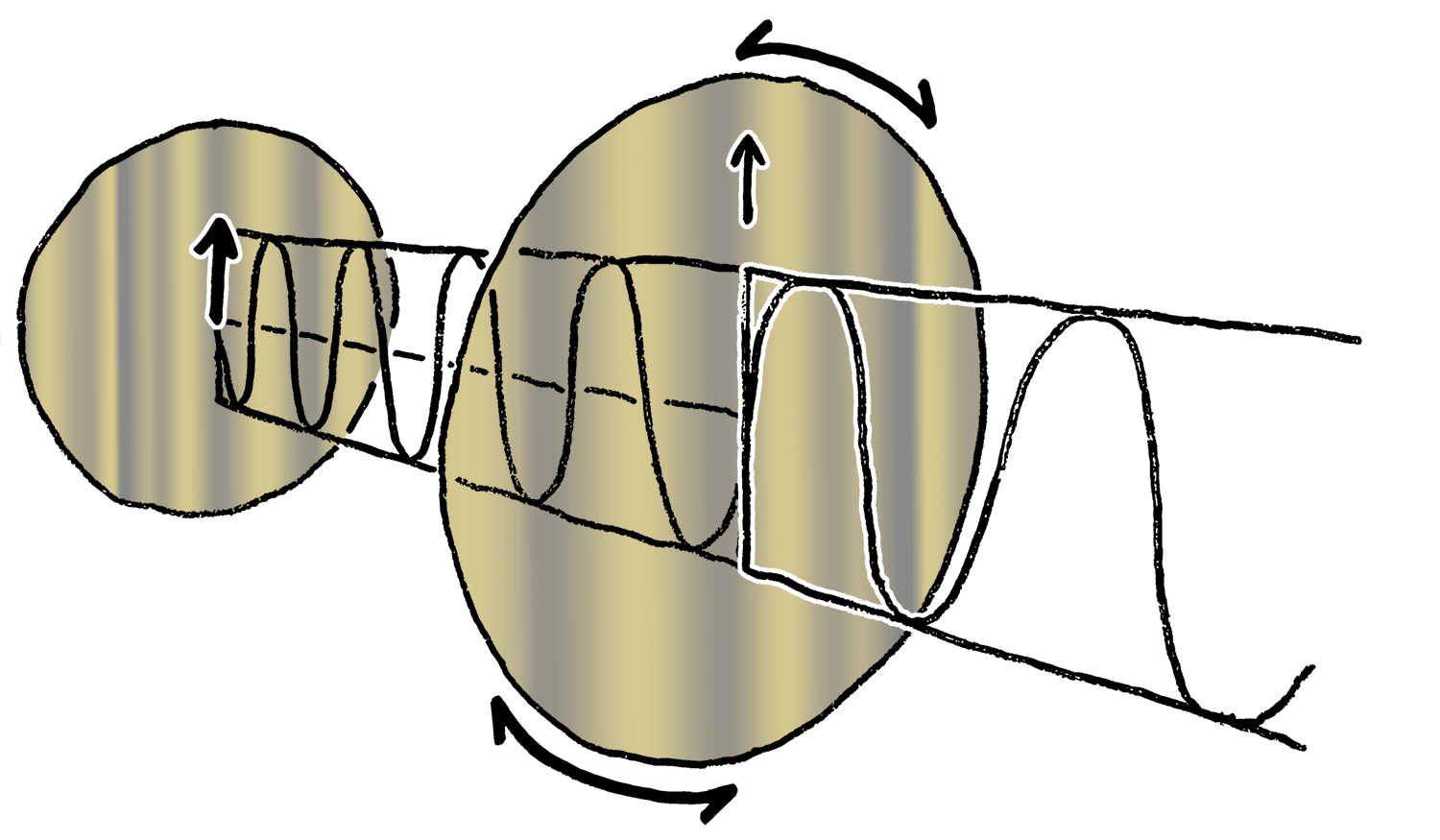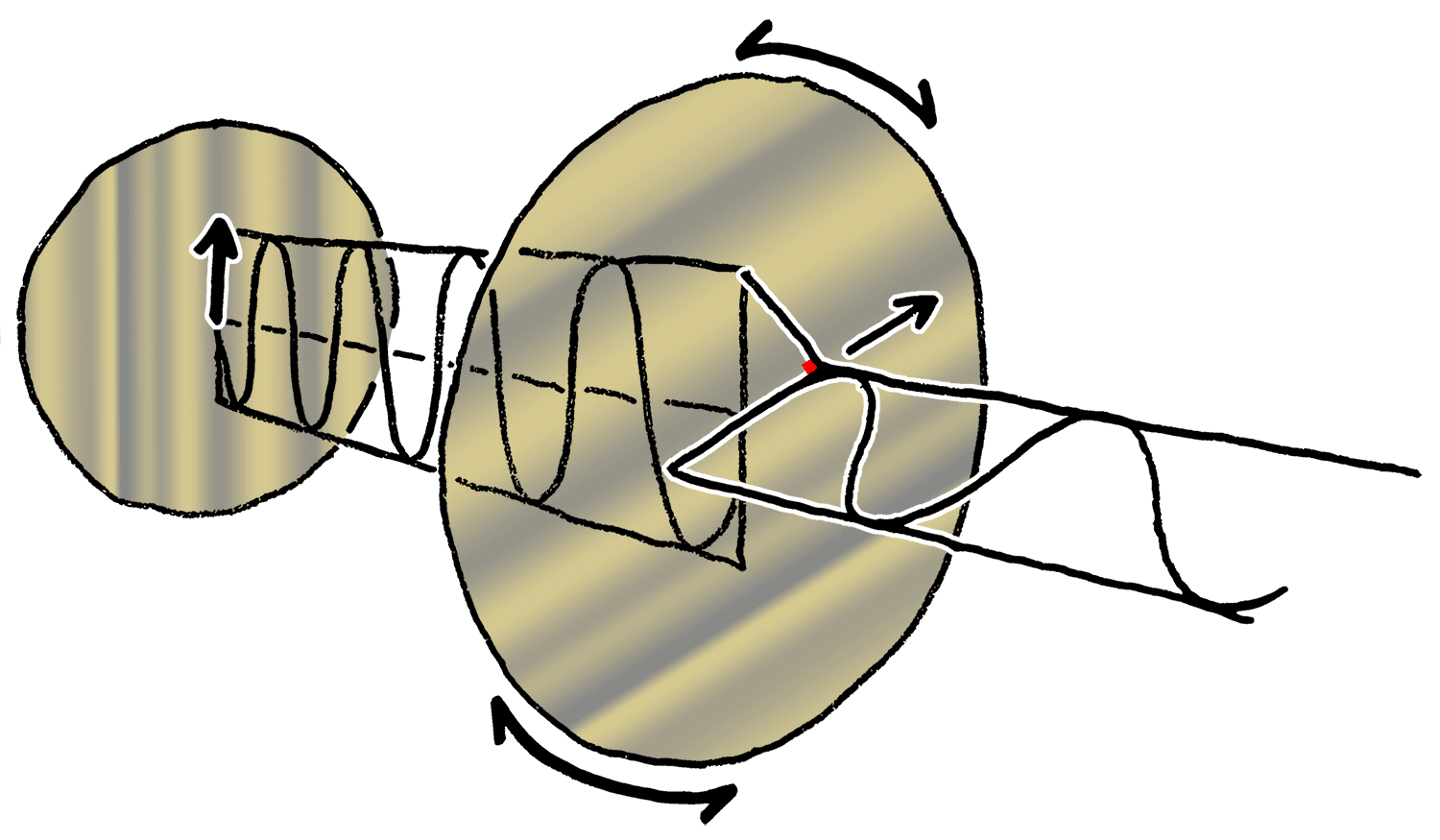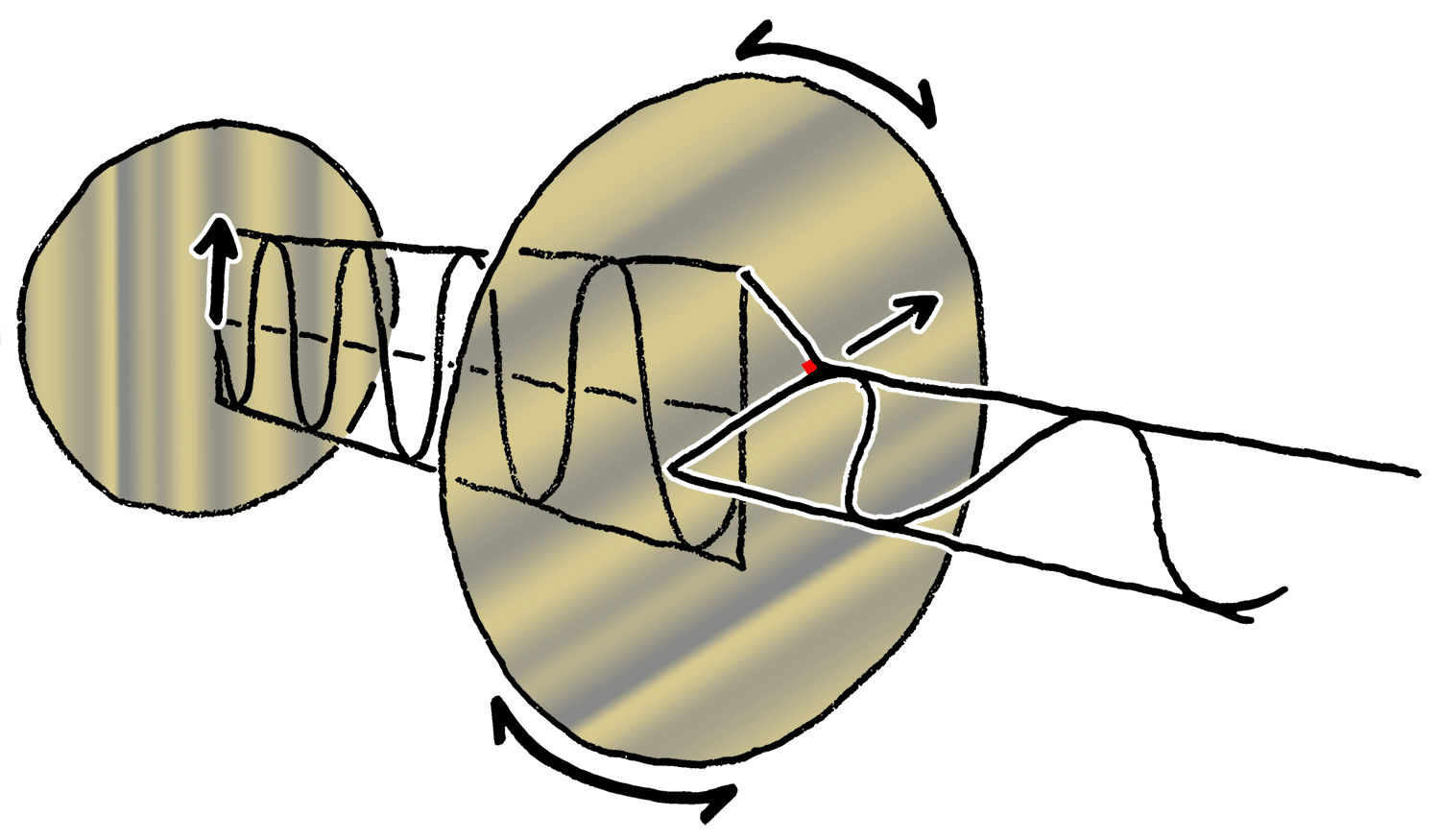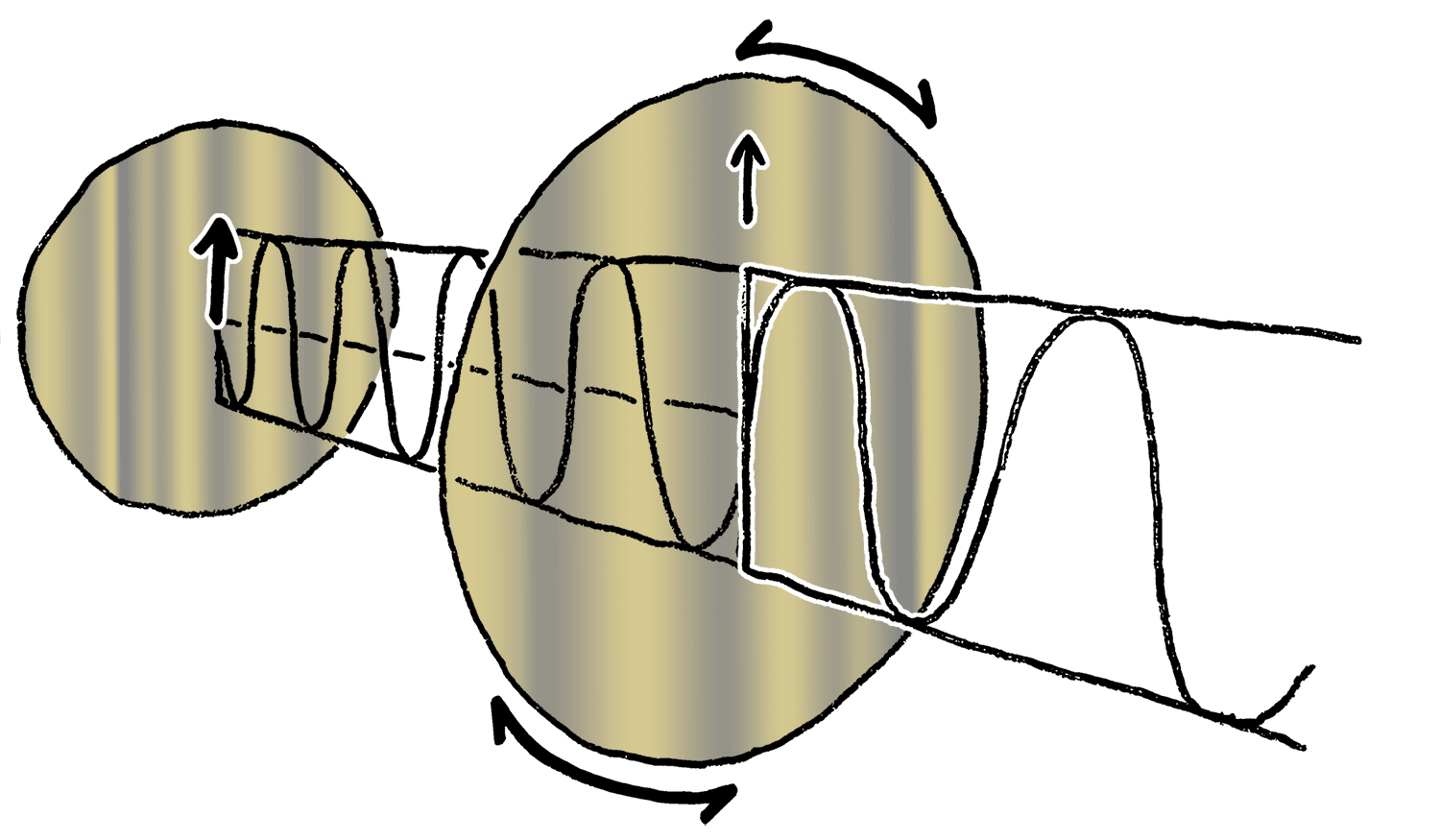
Light Polarization
Polarization ( also polarisation) is a property applying to transverse waves that specifies the geometrical orientation of the oscillations. In a transverse wave, the direction of the oscillation is perpendicular to the direction of motion of the wave. A simple example of a polarized transverse wave is vibrations traveling along a taut string ''(see image)''; for example, in a musical instrument like a guitar string. Depending on how the string is plucked, the vibrations can be in a vertical direction, horizontal direction, or at any angle perpendicular to the string. In contrast, in longitudinal waves, such as sound waves in a liquid or gas, the displacement of the particles in the oscillation is always in the direction of propagation, so these waves do not exhibit polarization. Transverse waves that exhibit polarization include electromagnetic waves such as light and radio waves, gravitational waves, and transverse sound waves (shear waves) in solids. An electromagnetic wav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poincaré Sphere (optics)
Polarization ( also polarisation) is a property applying to transverse waves that specifies the geometrical orientation of the oscillations. In a transverse wave, the direction of the oscillation is perpendicular to the direction of motion of the wave. A simple example of a polarized transverse wave is vibrations traveling along a taut string ''(see image)''; for example, in a musical instrument like a guitar string. Depending on how the string is plucked, the vibrations can be in a vertical direction, horizontal direction, or at any angle perpendicular to the string. In contrast, in longitudinal waves, such as sound waves in a liquid or gas, the displacement of the particles in the oscillation is always in the direction of propagation, so these waves do not exhibit polarization. Transverse waves that exhibit polarization include electromagnetic waves such as light and radio waves, gravitational waves, and transverse sound waves (shear waves) in solids. An electromagnetic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coset Space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group ''G'' is a non-empty manifold or topological space ''X'' on which ''G'' acts transitively. The elements of ''G'' are called the symmetries of ''X''. A special case of this is when the group ''G'' in question is the automorphism group of the space ''X'' – here "automorphism group" can mean isometry group, diffeomorphism group, or homeomorphism group. In this case, ''X'' is homogeneous if intuitively ''X'' looks locally the same at each point, either in the sense of isometry (rigid geometry), diffeomorphism (differential geometry), or homeomorphism (topology). Some authors insist that the action of ''G'' be faithful (non-identity elements act non-trivially), although the present article does not. Thus there is a group action of ''G'' on ''X'' which can be thought of as preserving some "geometric structure" on ''X'', and making ''X'' into a single ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rajiah Simon
Rajiah Simon, is a Professor of Physics at the Institute of Mathematical Sciences, Chennai, India. Rajiah Simon received the Shanti Swarup Bhatnagar Prize for Science and Technology in 1993 for pioneering work in Quantum optics. Simon and collaborators initiated the "Quantum theory of charged-particle beam optics", by working out the focusing action of a magnetic quadrupole using the Dirac Equation. R. Jagannathan, R. Simon, E. C. G. Sudarshan and N. Mukunda Narasimhaiengar Mukunda (born 25 January 1939, New Delhi, India) is an Indian theoretical physicist. Mukunda's higher education began at Delhi University, where he was granted a B.Sc. (Hon) degree in 1953. For his Ph.D. he studied at University ...Quantum theory of magnetic electron lenses based on the Dirac equation Physics Letters A, 134, 457-464 (1989). References External links [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lorentz Group
In physics and mathematics, the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical and quantum setting for all (non-gravitational) physical phenomena. The Lorentz group is named for the Dutch physicist Hendrik Lorentz. For example, the following laws, equations, and theories respect Lorentz symmetry: * The kinematical laws of special relativity * Maxwell's field equations in the theory of electromagnetism * The Dirac equation in the theory of the electron * The Standard Model of particle physics The Lorentz group expresses the fundamental symmetry of space and time of all known fundamental laws of nature. In small enough regions of spacetime where gravitational variances are negligible, physical laws are Lorentz invariant in the same manner as special relativity. Basic properties The Lorentz group is a subgroup of the Poincaré group—the group of all isometries of Minkowski spacetime. Lorentz transformations are, precisely, iso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |